Файл: Моделирование электродвигателя постоянного тока.docx

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«МУРМАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»


Кафедра электрооборудования судов


РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА

по дисциплине

Моделирование судового электрооборудования

Тема:

«Моделирование электродвигателя постоянного тока»

Вариант№7
Выполнил: студент

ЭСЭО18з-688

Ковалев К. А.

«___»_______________2023 г.

__________________(подпись)

Проверил: преподаватель

Саватеев Д. А.

«___»_______________2023г.

__________________(подпись)


Мурманск

2023

1.Паспортные данные электродвигателя………………………………………….	3
2.Математическая модель двигателя постоянного тока с независимым возбуждением…………………………………………………………………….....
	4
3. Расчет параметров схемы замещения…………………………………………..	5
4.Моделирование двигателя постоянного тока с использованием функционального блока библиотеки силовых устройств Simulink……………..
	9
5.Моделирование пуска двигателя постоянного тока с пониженным напряжением на якорной обмотке…………………………………………………
	14
6. Использование данных, полученных при моделировании……………………	15
7. Список литературы………………………………………………………………	22

Содержание

1. 
   Паспортные данные электродвигателя П52М.
   

Мощность: P = 8,8 кВт;

Напряжение: U = 220 В;

КПД: ???? = 0,825;

Номинальная скорость: n = 1500 об/мин;

Число пар полюсов: p = 4;

Сопротивление шутовой обмотки возбуждения:

---

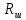
= 150 Ом;

Число витков якорной обмотки: 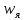= 248;

Сопротивление якорной обмотки: 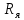= 0,19 Ом;

Сопротивление обмотки добавочных полюсов: 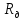= 0,084 Ом;

Число витков шунтовой обмотки возбуждения: 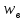= 1500;

Коэффициент рассеяния: sigma=1.12; .

2 Математическая модель двигателя постоянного тока с независимым возбуждением.

В основе моделирования двигателя постоянного тока с независимым возбуждением лежит решение системы дифференциальных уравнений, составленных по второму правилу Кирхгофа для двух цепей: цепи возбуждения и якорной цепи (рис. 1):


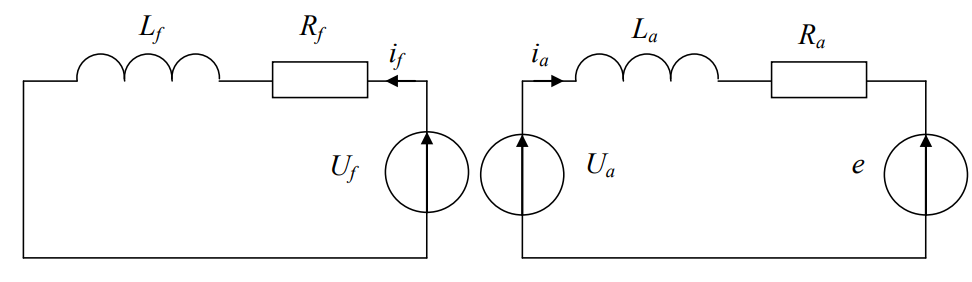
Рис.1.Схема замещения электрических цепей двигателя постоянного тока с независимым возбуждением.



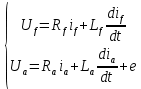
где e– функции времени.

ЭДС вращения:

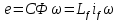
где 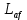- взаимная индуктивность якорной обмотки и обмотки возбуждения.

Угловая скорость является функцией времени и входит в уравнение, устанавливающее связь между механическими величинами:



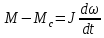
Электромагнитный момент двигателя:



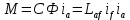
Таким образом, учитывая взаимное влияние механических и электромагнитных процессов, в систему необходимо включить три уравнения:



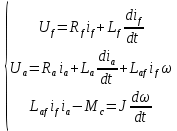
Полученная система уравнений является математической моделью двигателя, и, чтобы привести модель в действие, необходимо решить систему. Следует понимать, что особенность исследовательской деятельности заключается в том, чтобы использовать модель в действии многократно, меняя различные параметры. Один из способов реализовать такую возможность – запрограммировать решение уравнений в том или ином виде. Далее будет рассмотрено несколько способов такой реализации, но на предварительном этапе необходимо определить параметры схемы замещения по паспортным данным электродвигателя.

---

3. Расчет параметров схемы замещения.

3.1. Расчетные соотношения. Индуктивность якорной цепи:



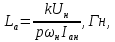
где 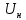- номинальное напряжение якорной обмотки, В;

p– число пар полюсов;

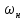– номинальная угловая скорость ротора, рад/с;

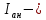номинальный ток якорной обмотки, А;

k = 0,6 для некомпенсированных двигателей.

Номинальная угловая скорость ротора рассчитывается по формуле:



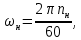
где 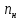– номинальная частота вращения ротора, об/мин;

Номинальный ток якоря является частью номинального тока электродвигателя:



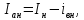
где 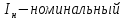ток электродвигателя, А;

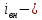номинальный шутовой обмотки возбуждения, А.

Номинальный ток электродвигателя:



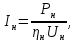
где 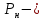номинальная мощность, Вт;

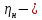номинальный коэффициент полезного действия (КПД).

Номинальный ток шунтовой обмотки возбуждения:



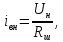
где – сопротивление шунтовой обмотки возбуждения, Ом.

Индуктивность шунтовой обмотки возбуждения:



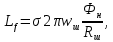
где =1,121,25 – коэффициент рассеяния магнитоного потока главного полюса;

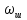– число витков шунтовой обмотки возбуждения;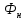

---

– номинальный магнитный поток на полюс, Вб.

Номинальный магнитный поток может быть выделен из произведения С :



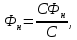
где С – машинная постоянная, вычисляемая, в свою очередь, по формуле:



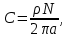
В формуле N – число активных проводников якорной обмотки, а – число пар параллельных ветвей якорной обмотки – каталожные значения. Если число активных проводников не задано, оно может быть вычислено как удвоенное количество витков якорной обмотки, через число секций и число витков секции – в зависимости от того, какие данные приведены в справочнике.

Произведение 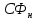вычисляется на основе номинальных данных: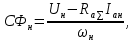



где 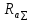- суммарное сопротивление якорной цепи, включающее в себя сопротивление якорной обмотки и сопротивление обмотки добавочных полюсов.

Взаимная индуктивность якорной обмотки и шунтовой обмотки возбуждения:



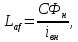
Коэффициент вязкого трения, определяющий момент холостого хода:


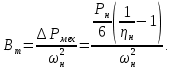
3.2. Автоматизация расчета параметров схемы замещения.

3.2.1. Автоматизация расчета с использованием М-функции.

М-функция представляет собой запрограммированные формулы написанных на языке программирования MATLAB, выполняемых последовательно, от первой до последней строки, при обращения пользователя к функции. Текст функции начинается со специального заголовка, обращение к функции может производиться из командной строки, М-сценария или другой функции, аргументы функции задаются при обращении к ней.

В работе требуется создать функцию, выполняющую расчет величин на основе паспортных и обмоточных данных электрической машины, ее написание следует начинать со строки вида:

---

function[L_a,L_f,L_af,B_m,M_n,i_f_n,I_a_n,omega_n]=dcm_parameters(P_n,U_n,n_n,kpd_n,p,a,J,R_a,R_add_p,R_f,w_a,w_f,sigma,k)
Слово function является специальным, о чем свидетельствует его синий цвет. После этого слова в квадратных скобках указываются величины, которые должны быть возвращены функцией при обращении к ней. Их принято называть выходными переменными функции. После знака "=" должно указываться название функции. В данном примере это название dcm_parameters, но может быть любым, подчиняющимся правилам обозначения переменных. За названием функции, в круглых скобках приводим входные аргументы функции – данные, на основании которых будет производиться расчет. Заданный заголовком порядок записи входных аргументов должен строго соблюдаться при обращении к функции. Запись заголовка функции в редакторе MATLAB должна быть выполнена в одной строке, без переноса. После заголовка должен располагаться основной программный код:



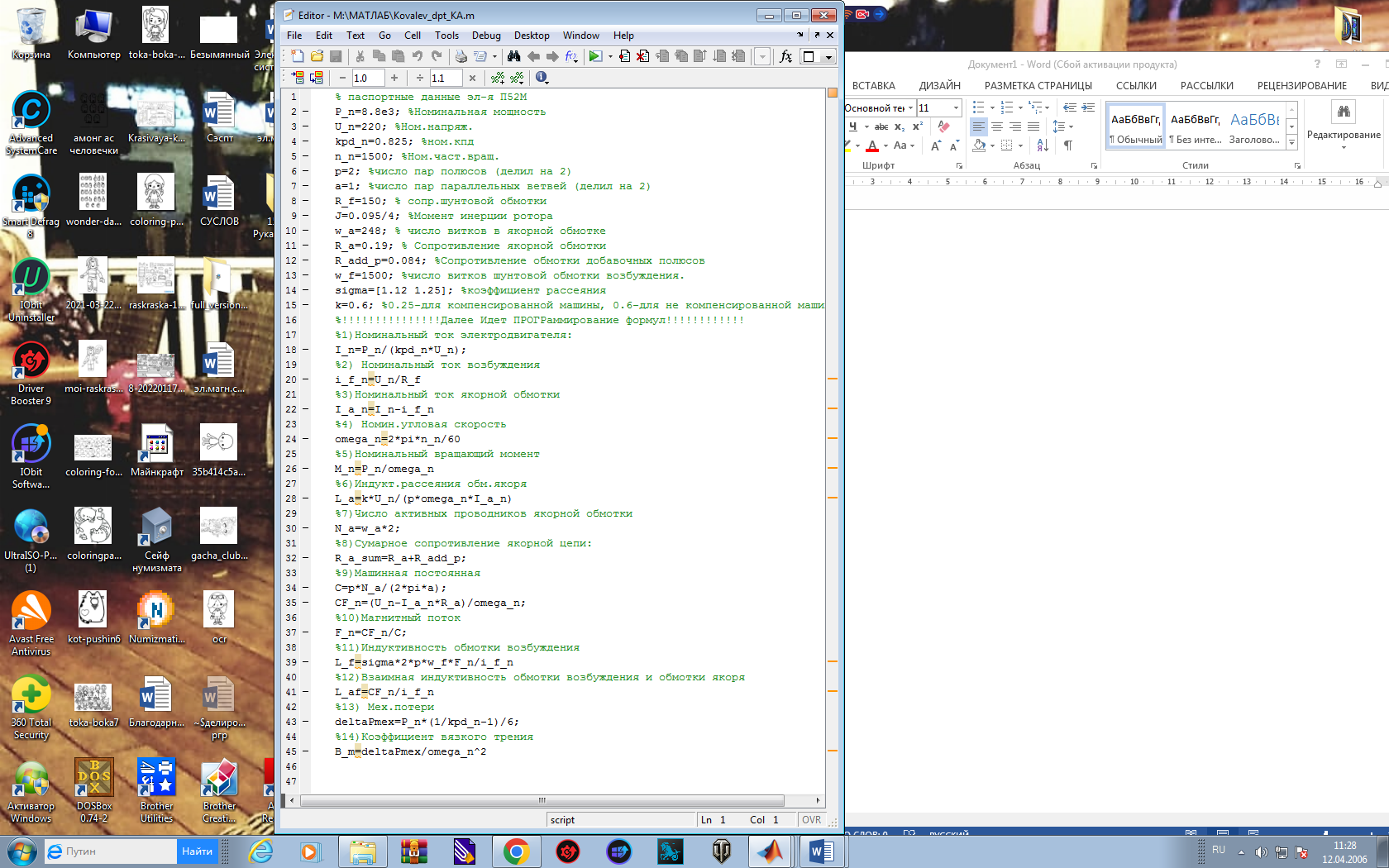
Результат выполнения функции будет выведен в командное окно:



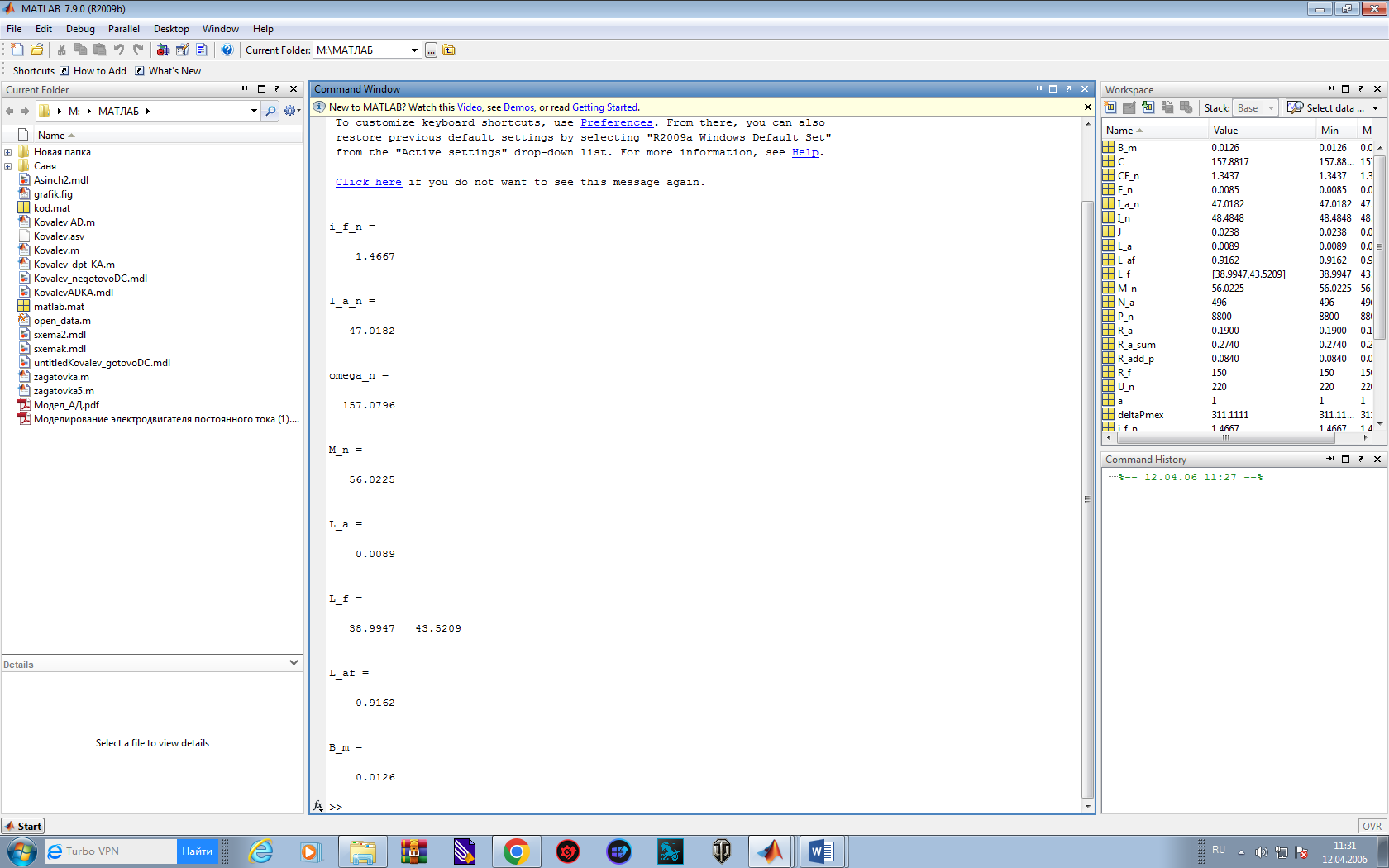
4. Моделирование двигателя постоянного тока с использованием функционального блока библиотеки силовых устройств Simulink.

Simulink – это система имитационного блочного моделирования динамических систем, являющаяся подсистемой MATLAB. Средства моделирования Simulink основываются на программных средствах MATLAB, но позволяют обойтись без использования в явном виде языка MATLAB и создавать модели из стандартных блоков в графическом виде.

4. 1. Моделирование прямого пуска двигателя постоянного тока.

Для решения задач моделирования систем, составной частью которых является двигатель постоянного тока, целесообразно использование готового блока: SimPowerSystems – Machines – DC machine


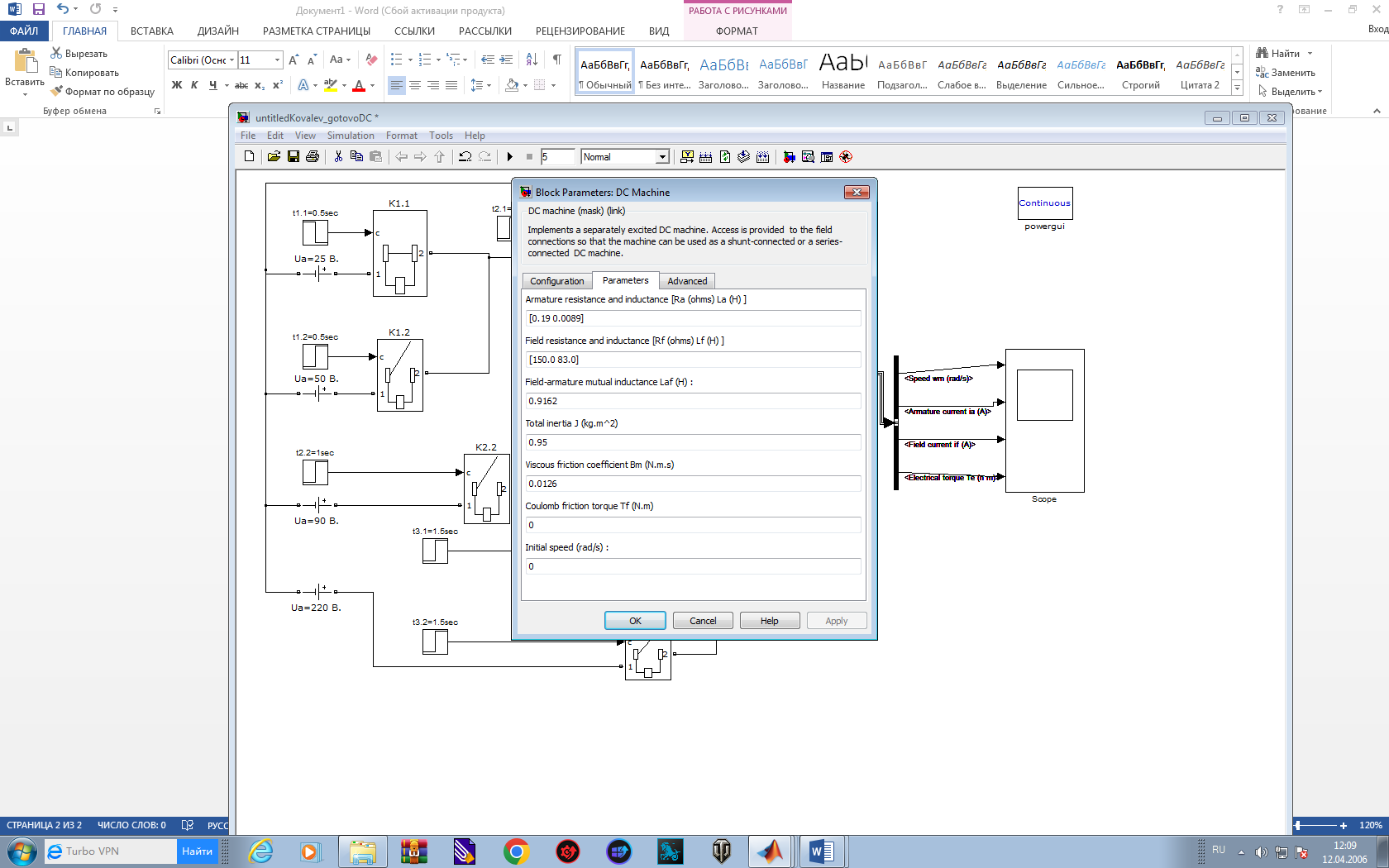
Рис.2. Функциональный блок DC machine и его окно параметров.


Помимо выводов обмоток электродвигателя, блок имеет вход TL и выход т. Вход TL блока предназначен для ввода момента сопротивления, выход m – для вывода величин, характеризующих работу двигателя. В окно

---