ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 61
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
параметров машины должны быть внесены данные, полученные на предварительном этапе расчета.
Сема установки, основным элементом которой является двигатель постоянного тока, представлена на рисунке 3.
Рис.3. Установка для пуска и исследования двиг. постоянного тока П41М.
Помимо машины пост. тока, в схеме используются следующие элементы:
- устройство для скачкообразного изменения величины: Step (Рис.4,а);
- источник питания постоянного тока, с возможностью изменять напряжение: Controlled Voltage Source (Рис.4, б);
- осциллограф: Scope (Рис.4, в);
- селектор сигналов Bus Selector (Рис.4, г);
Рис.4 Элементы моделирования установки для пуска и исследования двигателя постоянного тока.
Элемент Step скачкообразно изменяют значение, передаваемое на вход последующего блока, с Initial value на Final value в момент времени Step time (значение Sample time должно быть равно нулю). На рисунке 5 показано, что передаваемые значения 24,83 – для задания момента сопротивления на валу электродвигателя. Важно, чтобы момент сопротивления возникал позже сигналов питания обмоток двигателя, на рисунке показано, что эта задержка составляет 0,1 с. Настройка данного блока для источника питания обмотки возбуждения идентична настройке якорного блока.
Рис 5. Настройка элемента Step.
Среди настроек осциллографа в первую очередь следует уделить внимание количеству осей –Number of Axes, которое должно быть равно количеству сигналов, выбранных селектром сигналов, показываемому временному интервалу –Time Range, который должен быть равен времени симуляции, отсутствию ограничения числа последних, выводимых в координатные оси точек –Limit data points to last, наличию отметки о сохранении данных в рабочей области– Save data to workspace. Указанные настройки доступны в окне, закладки. Пределы по оси ординат настраиваются в контекстном меню конкретных осей
Завершающий этап настройки –задание параметров симуляции (рис. 6). Важно, чтобы был выбран наиболее подходящий метод решения системы дифференциальных уравнений – Solveroptions и установлено время симуляции– Simulation time – Stop time, соответствующее пределу по оси абсцисс осциллографа.
Рис.6 Настройки симуляции.
После запуска описанной модели в координатных осях осциллографа появились четыре сигнала описывающий прямой пуск электродвигателя.
Рис.7 Результат моделирования прямого пуска электродвигателя.
5. Моделирование пуска двигателя постоянного тока с пониженным
напряжением на якорной обмотке.
Рис.8 Модель установки, обеспечивающей пуск двигателя постоянного тока с пониженным напряжением на якорной обмотке.
Изменение напряжения питания якорной обмотки электродвигателя постоянного тока приводит к изменению частоты вращения идеального холостого хода этого двигателя и не меняет наклон его искусственной механической характеристики. Это значит, что жесткость характеристик остается высокой и при осуществлении пуска, для ограничения пускового тока и токов переключения на допустимом уровне потребуется высокая плавность изменения напряжения. Высокая плавность достигается увеличением числа ступеней регулирования. Плавность должна быть тем выше, чем жестче механические характеристики двигателя, то есть, чем больше его мощность. Результат моделирования четырехступенчатого пуска электродвигателя с пониженным напряжением на якорной обмотке. Рис. 8. Модель установки, обеспечивающей пуск двигателя постоянного тока с пониженным напряжением на якорной обмотке. Модель набрана из блоков, описанных ранее, основная настройка элементов указана в подписях под ними. На рис. 9 представлены осциллограммы пуска.
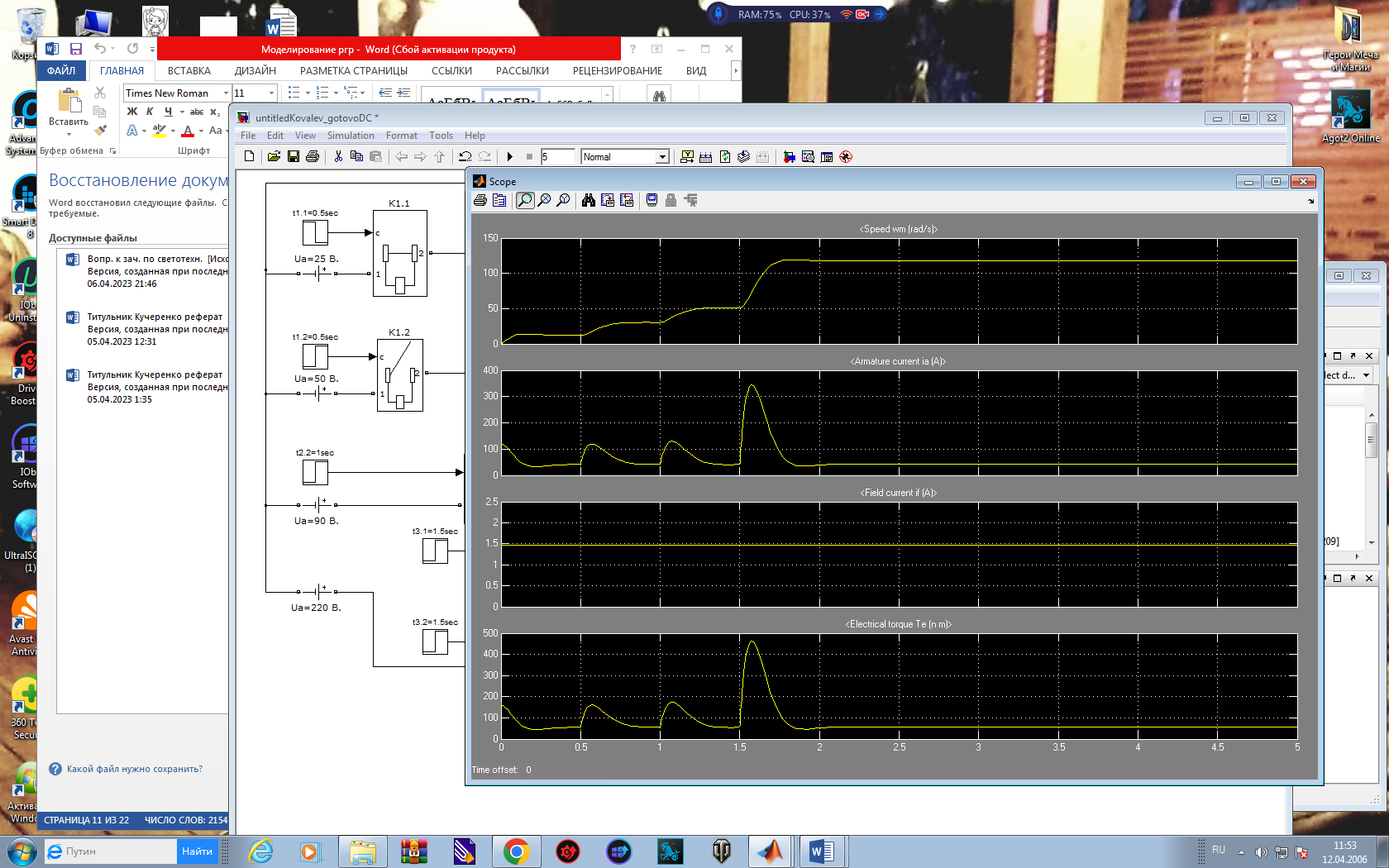
Рис.9 Результат моделирования четырехступенчатого пуска электродвигателя с пониженным напряжением на якорной обмотке.
6. Использование данных, полученных при моделировании.
6.1.Извлечение данных.
Построение графиков в координатных осях осциллографа ведется по точкам, координаты которых хранятся в структуре, называемой по умолчанию ScopeData. В том, что такая структура создается можно убедиться, просмотрев рабочую область MATLAB (Рис.10). Для просмотра структуры, в командной строке MATLAB следует ввести ее название. На рисунке 10, показано, что структура содержит три элемента: числовой массив значений времени, объединенные в структуру данные о сигналах и название блока.
Рис.10 Структура ScopeData.
Для удобства работы с полученными данными целесообразно представить х в виде двумерного массива, первая строка которого – время, остальные –значения величин, выводимых в координатные оси осциллографа. Следующая функция переформатирует вывод данных:
1.function data=open_data(DataName)
2.signals=DataName.signals;
3.n=length(DataName.signals);
4.data(1,:)=(DataName.time)';
5.for k=1:1:n6 data(1+k,:)=(signals(k).values)';
7.end
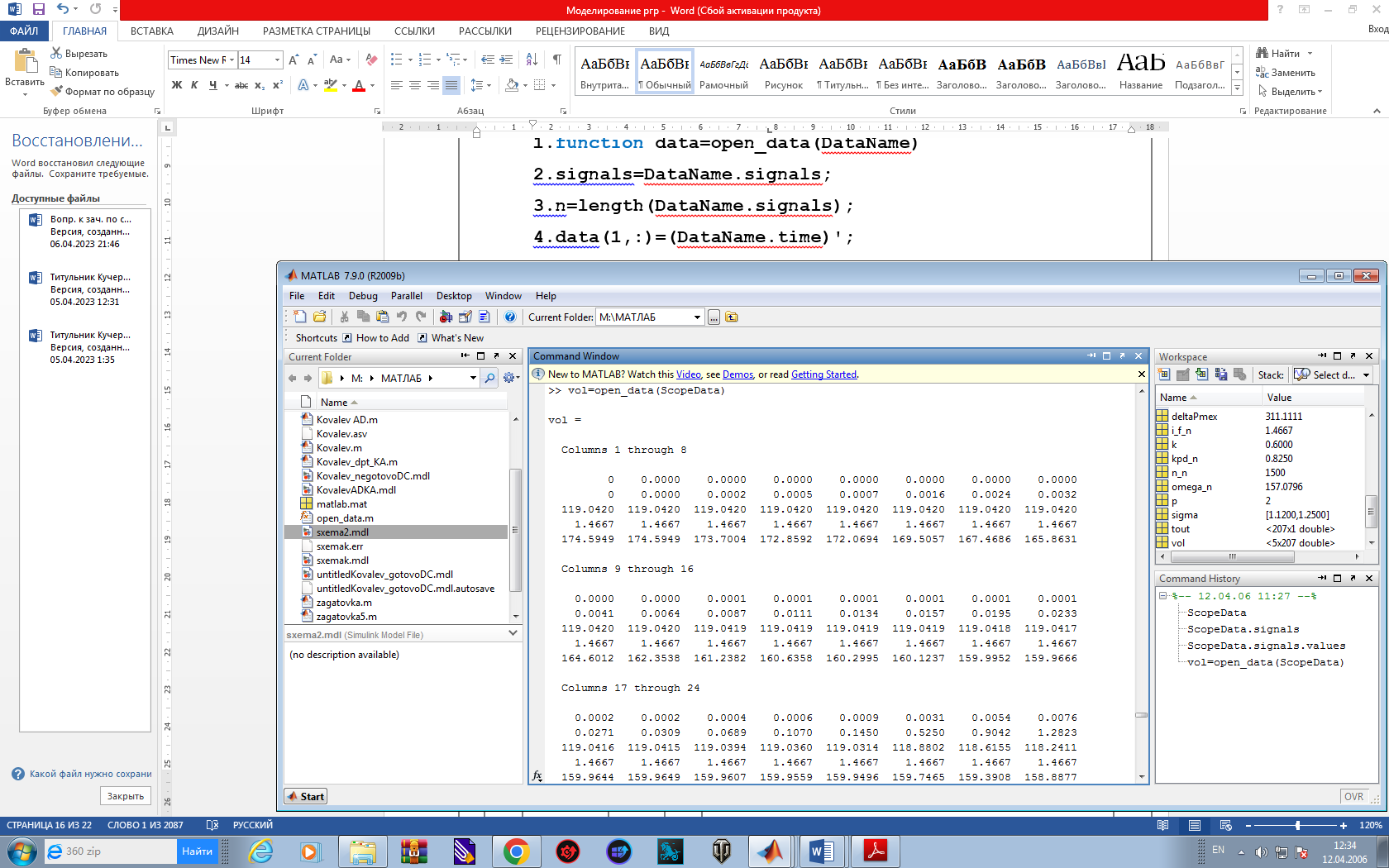
Рис. 11 Массив Данных.
В 4-й строке представленной функции содержатся инструкции, заполняющие первую строку массива data значениями моментов времени, в цикле 5-7 – значениями контролируемых величин. Функция должна быть сохранена в каталоге, находящемся на пути доступа MATLAB. При обращении к функции в скобках должно быть указано название структуры, в которой сохранены данные моделирования.
6.2. Определение максимального значения величины. Например, для определения максимального значения тока якоря следует, после выполнения описанных ранее действий, набрать в командной строке:
>> Ia_max = max(vol(3,:))
Ia_max = 46,6667
Функция MATLAB max возвращает максимальное значение элемента в массиве, указанном в качестве аргумента функции. В данном случае это третья строка двумерного массива vol. Максимальное значение, которое принимал ток якорной обмотки за время пуска, равно 46,6667 А
6.3. Определение момента времени, в который величина достигает максимального значения.
Искомый момент времени может быть получен по индексу максимального значения тока:
>> i_Ia_max=find(vol(3,:)= Ia_max)
i_Ia_max = 2
Функция MATLAB find возвращает индекс элемента массива vol (3,:) , удовлетворяющего условию равенства определенному ранее максимальному
значению тока якорной обмотки. Этот индекс – 2. Индекс момента времени, в который якорный ток достигает максимума, совпадает с индексом этого значения тока:
>> t_Ia_max = vol(1,149)
t_Ia_max = 1.2321
Запись vol(1,149) соответствует обращению к 149 элементу первой строки массива данных vol.
6.4. Построение динамических механических характеристик электродвигателя.
Механические характеристики электродвигателя строятся в координатах М-. Это значит, что в качестве первого аргумента функции plot должна быть указана строка значений электромагнитного момента, а в качестве второго аргумента – строка значений угловой скорости:
>> plot(vol(5,:),vol(2,:))
Следующие команды добавляют координатную сетку, включают режим добавления последующего графика к предыдущему и наносят на координатную плоскость за характеристику момента нагрузки:
>> grid on>> hold on>> plot([13 13],[0 160],'r')
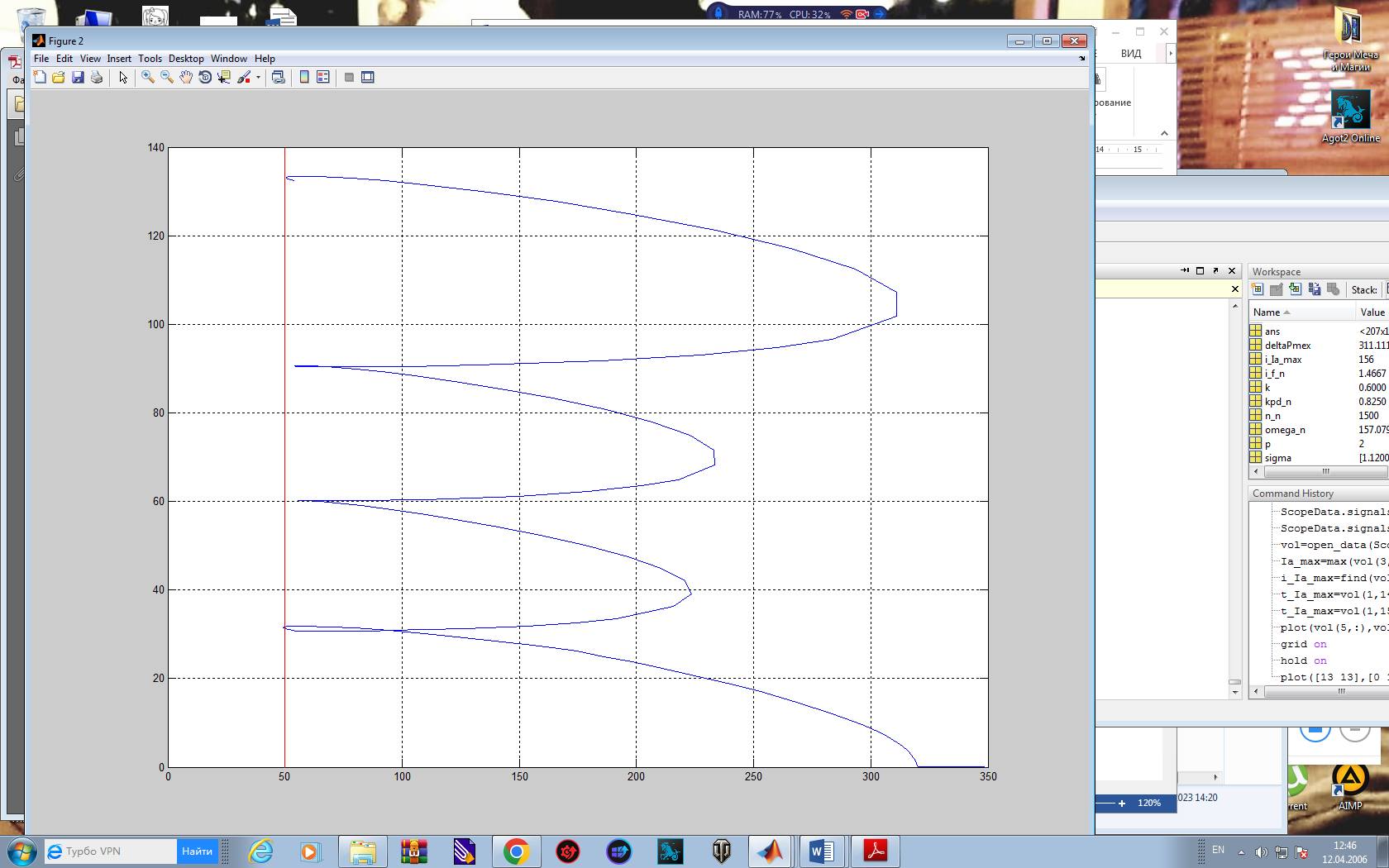
Рис. 13 Динамические механические характеристики электродвигателя.
6.5. Расчет тепловых потерь в пусковом реостате. В соответствии с законом Джоуля-Ленца тепловые потери в сопротивлении R определяются как
где i=f(t) – изменяющийся, в общем случае, ток; t1 и t2 – моменты времени, определяющие временной интервал, в течение которого происходит выделение тепла. При выполнении компьютерного моделирования шаг итерации настолько мал, что с достаточной для инженерных расчетов точностью можно заменить интеграл конечной суммой:
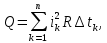
где п – количество итераций, k – номер итерации,tk – k-й временной интервал,
ik – ток, принимаемый неизменным на k-м временном интервале.
Ток якорной обмотки протекает по пусковому сопротивлению первые 0,8секунды, поэтому для расчета следует использовать только данные, соответствующие периоду времени от 0 до 0,8 с. Для получения индексов элементов массива моментов времени, соответствующих разгону по пусковой характеристике, следует воспользоваться функцией find:
>> i_pusk=find(vol(1,:)<=2.0)
В полученном массиве временных интервалов 88 элементов. Это значит, что при программировании формулы (28) необходимо использовать элементы массива значений тока якоря с этими же номерами:
>> Q=sum(vol(3,1:92).^2*4.*d_t)
Q =1.5905e+004
Поскольку при оплате электроэнергии в качестве единицы ее измерения применяются киловатт-часы, представляет интерес перевод результата, полученного в Джоулях, в кВтч:
>> W=Q*0.278e-6
W =0.0044
Полученное значение очень невелико, но и временной интервал, за который выделилась эта энергия, составляет всего 0,8 секунды.
При использованииреостатного регулирования частоты вращения электродвигателя, работающего в повторно-кратковременном режиме, переходные процессы составляют значительную часть рабочего цикла, и потери энергии в реостатах могут оказаться очень существенными. Таким образом, можно заключить, что полученные при моделировании данные о величинах, характеризующих электрическую машину, являются исходным материалом для ее дальнейшего исследования и оптимизации режимов ее работы, а приведенные примеры обработки результатов не исчерпывают всех возможных задач исследования.
1. Герман-Галкин С. Г. MATLAB & Simulink. Проектирование мехатронныхсистем на ПК. – СПб.: Издательство "Корона. Век", 2011. – 368 с., ил.
2. Судовые электроприводы : Справочник. В 2-х томах. / [А. П. Богословский, Е. М. Певзнер, И. Р. Фрейдзон, А. Г. Яуре; Науч. ред. А. К. Юдин].– 2-е изд., перераб. и доп. – Л. : Судостроение, 1983. Т. 1. 5. Вешкельский С. А. Справочник судового дизелиста. Вопросы и ответы. — Л.: Судостроение, 1990. — 368 с.: ил.
Сема установки, основным элементом которой является двигатель постоянного тока, представлена на рисунке 3.Рис.3. Установка для пуска и исследования двиг. постоянного тока П41М.
Помимо машины пост. тока, в схеме используются следующие элементы:
- устройство для скачкообразного изменения величины: Step (Рис.4,а);
- источник питания постоянного тока, с возможностью изменять напряжение: Controlled Voltage Source (Рис.4, б);
- осциллограф: Scope (Рис.4, в);
- селектор сигналов Bus Selector (Рис.4, г); Рис.4 Элементы моделирования установки для пуска и исследования двигателя постоянного тока.
Элемент Step скачкообразно изменяют значение, передаваемое на вход последующего блока, с Initial value на Final value в момент времени Step time (значение Sample time должно быть равно нулю). На рисунке 5 показано, что передаваемые значения 24,83 – для задания момента сопротивления на валу электродвигателя. Важно, чтобы момент сопротивления возникал позже сигналов питания обмоток двигателя, на рисунке показано, что эта задержка составляет 0,1 с. Настройка данного блока для источника питания обмотки возбуждения идентична настройке якорного блока.Рис 5. Настройка элемента Step.
Среди настроек осциллографа в первую очередь следует уделить внимание количеству осей –Number of Axes, которое должно быть равно количеству сигналов, выбранных селектром сигналов, показываемому временному интервалу –Time Range, который должен быть равен времени симуляции, отсутствию ограничения числа последних, выводимых в координатные оси точек –Limit data points to last, наличию отметки о сохранении данных в рабочей области– Save data to workspace. Указанные настройки доступны в окне, закладки. Пределы по оси ординат настраиваются в контекстном меню конкретных осей
Завершающий этап настройки –задание параметров симуляции (рис. 6). Важно, чтобы был выбран наиболее подходящий метод решения системы дифференциальных уравнений – Solveroptions и установлено время симуляции– Simulation time – Stop time, соответствующее пределу по оси абсцисс осциллографа.
Рис.6 Настройки симуляции. После запуска описанной модели в координатных осях осциллографа появились четыре сигнала описывающий прямой пуск электродвигателя.Рис.7 Результат моделирования прямого пуска электродвигателя.
5. Моделирование пуска двигателя постоянного тока с пониженным
напряжением на якорной обмотке.
Рис.8 Модель установки, обеспечивающей пуск двигателя постоянного тока с пониженным напряжением на якорной обмотке.
Изменение напряжения питания якорной обмотки электродвигателя постоянного тока приводит к изменению частоты вращения идеального холостого хода этого двигателя и не меняет наклон его искусственной механической характеристики. Это значит, что жесткость характеристик остается высокой и при осуществлении пуска, для ограничения пускового тока и токов переключения на допустимом уровне потребуется высокая плавность изменения напряжения. Высокая плавность достигается увеличением числа ступеней регулирования. Плавность должна быть тем выше, чем жестче механические характеристики двигателя, то есть, чем больше его мощность. Результат моделирования четырехступенчатого пуска электродвигателя с пониженным напряжением на якорной обмотке. Рис. 8. Модель установки, обеспечивающей пуск двигателя постоянного тока с пониженным напряжением на якорной обмотке. Модель набрана из блоков, описанных ранее, основная настройка элементов указана в подписях под ними. На рис. 9 представлены осциллограммы пуска.
Рис.9 Результат моделирования четырехступенчатого пуска электродвигателя с пониженным напряжением на якорной обмотке.
6. Использование данных, полученных при моделировании.
6.1.Извлечение данных.
Построение графиков в координатных осях осциллографа ведется по точкам, координаты которых хранятся в структуре, называемой по умолчанию ScopeData. В том, что такая структура создается можно убедиться, просмотрев рабочую область MATLAB (Рис.10). Для просмотра структуры, в командной строке MATLAB следует ввести ее название. На рисунке 10, показано, что структура содержит три элемента: числовой массив значений времени, объединенные в структуру данные о сигналах и название блока.
Рис.10 Структура ScopeData.
Для удобства работы с полученными данными целесообразно представить х в виде двумерного массива, первая строка которого – время, остальные –значения величин, выводимых в координатные оси осциллографа. Следующая функция переформатирует вывод данных:
1.function data=open_data(DataName)
2.signals=DataName.signals;
3.n=length(DataName.signals);
4.data(1,:)=(DataName.time)';
5.for k=1:1:n6 data(1+k,:)=(signals(k).values)';
7.end
Рис. 11 Массив Данных.
В 4-й строке представленной функции содержатся инструкции, заполняющие первую строку массива data значениями моментов времени, в цикле 5-7 – значениями контролируемых величин. Функция должна быть сохранена в каталоге, находящемся на пути доступа MATLAB. При обращении к функции в скобках должно быть указано название структуры, в которой сохранены данные моделирования.
6.2. Определение максимального значения величины. Например, для определения максимального значения тока якоря следует, после выполнения описанных ранее действий, набрать в командной строке:
>> Ia_max = max(vol(3,:))
Ia_max = 46,6667
Функция MATLAB max возвращает максимальное значение элемента в массиве, указанном в качестве аргумента функции. В данном случае это третья строка двумерного массива vol. Максимальное значение, которое принимал ток якорной обмотки за время пуска, равно 46,6667 А
6.3. Определение момента времени, в который величина достигает максимального значения.
Искомый момент времени может быть получен по индексу максимального значения тока:
>> i_Ia_max=find(vol(3,:)= Ia_max)
i_Ia_max = 2
Функция MATLAB find возвращает индекс элемента массива vol (3,:) , удовлетворяющего условию равенства определенному ранее максимальному
значению тока якорной обмотки. Этот индекс – 2. Индекс момента времени, в который якорный ток достигает максимума, совпадает с индексом этого значения тока:
>> t_Ia_max = vol(1,149)
t_Ia_max = 1.2321
Запись vol(1,149) соответствует обращению к 149 элементу первой строки массива данных vol.
Рис. 12. Данные полученные при моделирование.
6.4. Построение динамических механических характеристик электродвигателя.
Механические характеристики электродвигателя строятся в координатах М-. Это значит, что в качестве первого аргумента функции plot должна быть указана строка значений электромагнитного момента, а в качестве второго аргумента – строка значений угловой скорости:
>> plot(vol(5,:),vol(2,:))
Следующие команды добавляют координатную сетку, включают режим добавления последующего графика к предыдущему и наносят на координатную плоскость за характеристику момента нагрузки:
>> grid on>> hold on>> plot([13 13],[0 160],'r')
Рис. 13 Динамические механические характеристики электродвигателя.
6.5. Расчет тепловых потерь в пусковом реостате. В соответствии с законом Джоуля-Ленца тепловые потери в сопротивлении R определяются как
где i=f(t) – изменяющийся, в общем случае, ток; t1 и t2 – моменты времени, определяющие временной интервал, в течение которого происходит выделение тепла. При выполнении компьютерного моделирования шаг итерации настолько мал, что с достаточной для инженерных расчетов точностью можно заменить интеграл конечной суммой:
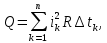
где п – количество итераций, k – номер итерации,tk – k-й временной интервал,
ik – ток, принимаемый неизменным на k-м временном интервале.
Ток якорной обмотки протекает по пусковому сопротивлению первые 0,8секунды, поэтому для расчета следует использовать только данные, соответствующие периоду времени от 0 до 0,8 с. Для получения индексов элементов массива моментов времени, соответствующих разгону по пусковой характеристике, следует воспользоваться функцией find:
>> i_pusk=find(vol(1,:)<=2.0)
В полученном массиве временных интервалов 88 элементов. Это значит, что при программировании формулы (28) необходимо использовать элементы массива значений тока якоря с этими же номерами:
>> Q=sum(vol(3,1:92).^2*4.*d_t)
Q =1.5905e+004
Поскольку при оплате электроэнергии в качестве единицы ее измерения применяются киловатт-часы, представляет интерес перевод результата, полученного в Джоулях, в кВтч:
>> W=Q*0.278e-6
W =0.0044
Полученное значение очень невелико, но и временной интервал, за который выделилась эта энергия, составляет всего 0,8 секунды.
При использованииреостатного регулирования частоты вращения электродвигателя, работающего в повторно-кратковременном режиме, переходные процессы составляют значительную часть рабочего цикла, и потери энергии в реостатах могут оказаться очень существенными. Таким образом, можно заключить, что полученные при моделировании данные о величинах, характеризующих электрическую машину, являются исходным материалом для ее дальнейшего исследования и оптимизации режимов ее работы, а приведенные примеры обработки результатов не исчерпывают всех возможных задач исследования.
Список литературы
1. Герман-Галкин С. Г. MATLAB & Simulink. Проектирование мехатронныхсистем на ПК. – СПб.: Издательство "Корона. Век", 2011. – 368 с., ил.
2. Судовые электроприводы : Справочник. В 2-х томах. / [А. П. Богословский, Е. М. Певзнер, И. Р. Фрейдзон, А. Г. Яуре; Науч. ред. А. К. Юдин].– 2-е изд., перераб. и доп. – Л. : Судостроение, 1983. Т. 1. 5. Вешкельский С. А. Справочник судового дизелиста. Вопросы и ответы. — Л.: Судостроение, 1990. — 368 с.: ил.