Файл: Методические указания по их выполнению по разделам цепей постоянных, синусоидальных и трехфазных токов.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 229
Скачиваний: 1
СОДЕРЖАНИЕ
Введение………………………………………………………………………………………4
1. Общие методические указания и правила
проведения лабораторных работ………………………………………………………4
2. Указания к монтажу схем лабораторных работ…………………………………...4
3. Правила техники безопасности в лаборатории электротехники………………….5
Лабораторная работа №1……………………………………………………………………. 6
Лабораторная работа №2…………………………………………………………………....15
Лабораторная работа №3…………………………………………………………………....20
Лабораторная работа №4……………………………………………………………………25
Лабораторная работа №5……………………………………………………………………33
Лабораторная работа №6……………………………………………………………………40
Лабораторная работа №7……………………………………………………………………50
Лабораторная работа №8……………………………………………………………………56
Исследование режимов работы линии передачи постоянного тока с помощью схемы замещения
Основные теоретические сведения
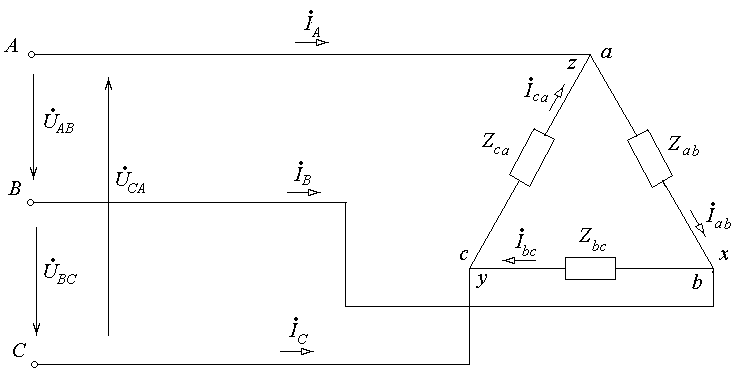
Рис.7-1. Схема соединения приемников треугольником
и включение их в трехфазную сеть.
Если комплексные сопротивления фаз нагрузки одинаковы
ZAB = ZBC = ZCA = zejφ , (7.1)
то такую нагрузку называют симметричной.
При соединении треугольником каждый приемник включен между подводящими проводами и находится под линейным напряжением, которое одновременно является фазным напряжением UФ. Поэтому при соединении приемников треугольником справедливо равенство
UФ = UЛ. (7.2)
Ток каждого приемника, входящего в соединение треугольником, является фазным и определяется по формуле
IФ = UФ/ZФ , (7.3)
где UФ - фазное напряжение на зажимах данного приемника, ZФ - его полное сопротивление.
При симметричной нагрузке фазные токи всех фаз одиноковы по величине
IAB = IBC = ICA = IФ (7.4)
и сдвинуты по отношению к своим фазным напряжениям на одинаковые углы
АВ = ВС = СА = , (7.5)
определяемые формулой
= arctg(xф/rф) , (7.6)
где xф- реактивное сопротивление фазы нагрузки, rф- ее активное сопротивление.
В общем случае линейные токи IA , IB , ICи фазные токи IAB , IBC , ICA связаны на основании первом закона Кирхгофа векторными уравнениями
IA= IAB - ICA;
IB= IBC - IAB; (7.7)
IC= ICA - IBC .
Из этих уравнений вытекает, что независимо от характера нагрузки всегда справедливо равенство
IA + IB + IC =0 (7.8)
При симметричной нагрузке фаз все линейные токи равны между собой и превышают значения фазных токов в
IЛ=
Векторы линейных напряжений могут изображаться либо симметричной звездой , либо равносторонним треугольником. Эти напряжения практически неизменны.
При симметричной нагрузке фаз векторы линейных токов сдвинуты относительно векторов фазных токов на 30° (pиc.7-2).
Фазные токи сдвинуты относительно фазных напряжений на одинаковые углы , а линейные токи определяются как геометрические разности соответствующих фазных токов (рис.7-2а).
При несимметричной нагрузке фаз, имеющей место при несоблюдении равенства (7.1) , нарушается симметрия как фазных, так и линейных токов, что видно из векторной диаграммы напряжений токов (рис.7-2б).
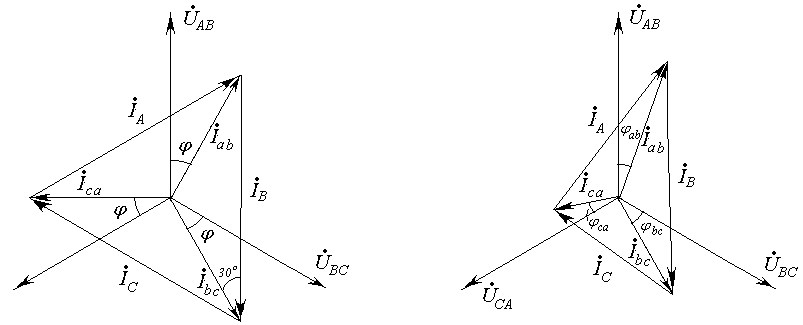
а) б)
Рис.7-2. Векторная диаграмма напряжений и токов при: а) при симметричной нагрузке, б) несимметричной нагрузке
Обрыв одного из линейных проводов нарушает нормальный режим работы установки, при этом приемники только одной фазы будут находиться под номинальным фазным напряжением, а приемники двух других фаз окажутся последовательно соединенными и будут питаться от этого же напряжения, которое обусловит установление на их зажимах напряжений, прямо пропорциональных величинам полных их сопротивлений. Следовательно, эти приемники окажутся под напряжением , отличающимся от номинального значения фазного напряжения. В случае преобладания в одной из фазиндуктивной, а в другой - емкостной нагрузки может возникнуть резонанс напряжений, сопровождающийся появлением повышенных напряжений , на зажимах реактивных приемников и резким увеличением тока.
На схеме (рис.7-3) показан обрыв линейного провода А. В фазе ВС напряжения и тока сохраняются такими же , как в цепи без обрыва , а в фазах АВ и СА становятся обратными по отношению к схеме (рис.7-1).
Из схемы (рис.7-3) следует:
UВС=UВА + UАС (7.10)
Фазы нагрузки АВ и СА соединены последовательно , по этому фазные токи равны:
IAB = ICA
Применяя (7.7) к схеме (рис.7-3) , получим:
IA
= -IAB- (-ICA) = -IAB+ ICA=0;
IB= IBC - (-IAB) = IBC + IAB; (7.11)
IC= -ICA - IBC = - ( IBC + IСА)= - IB.
Векторная диаграмма (рис.7-2б) преобразуется для схемы (рис.7-3) в другую форму (рис.7-4).
Активная мощность однофазных приемников, соединенных треугольником, может быть выражена так
Р=UACIAcos(UAC^IA)+UBCIBcos(UBC^IB) (7.12)
Трехфазная цепь соединенная треугольником , является трехпроводной. В такой цепи , независимо от способа соединение потребителя , активная мощность может быть измеренна как алгебраическая сумма показаний двух ваттметров (рис.7-5)
P = PW1 + PW2 (7.13)
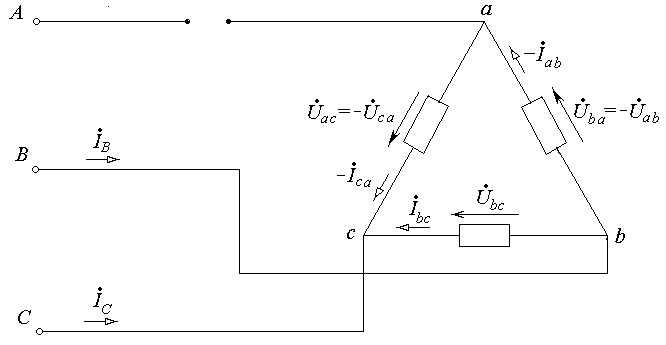
Рис.7-3.Схема соединения потребителя треугольником с
оборванным линейным проводом А
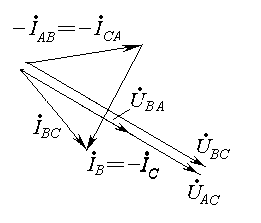
Рис.7-4. Векторная диаграмма напряжений и токов при обрыве линейного провода А (несимметричная нагрузка)
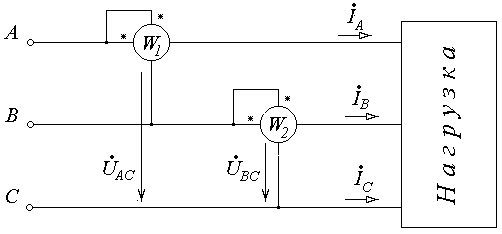
Рис.7-5 . Схема измерения активной мощности в трехфазной
сети с помощью двух ваттметров
Перечень оборудования
-
Источник трехфазного тока UЛ = 220 В, UФ = 127 В. -
Блок с ламповыми реостатами. -
Катушка индуктивности. -
Батарея конденсаторов. -
Амперметры - 6 штук с пределом измерений 2 А. -
Вольтметр с пределом измерений 250 В.
Содержание работы
Исследовать процессы в трехфазной цепи, соединенной треугольником при симметричной и несимметричной нагрузках, обрыве линейного провода. Измерить активную мощность трехфазной цепи с помощью двух ваттметров. По результатам измерений построить векторные диаграммы.
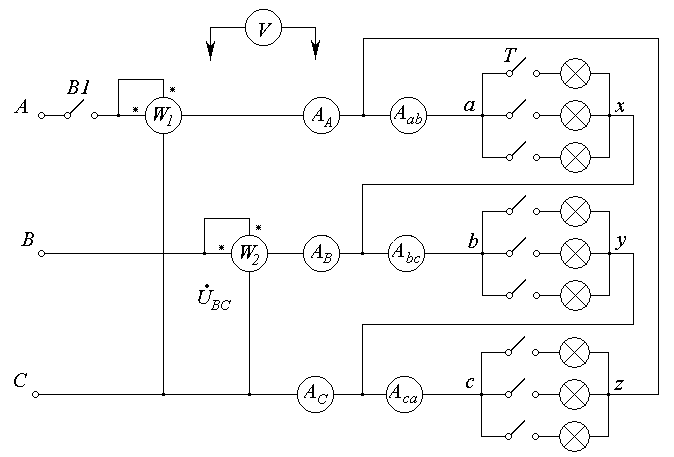
Рис.7-6. Схема исследования трехфазной цепи при соединении
приемников треугольником.
Порядок выполнения работы
-
Чисто активная нагрузка-
Собрать схему исследования (рис.7-6). Нагрузкой служат ламповые реостаты. Ключ В1 замкнут.
-
2. Установить нагрузку фаз симметричной (включить все тумблеры). С помощью вольтметров, с пределом измерений 250 В измерить напряжения между точками АВ , ВС , СА на нагрузке.
3. Не изменяя нагрузку , создать аварийный режим работы трехфазной цепи - обрыв линейного провода А (ключ В1 разомкнуть). Повторить измерения по п. 2.
4. Создать несимметричную нагрузку фаз (ключ В1 замкнуть) , включив разное количество ламп в фазах. Не изменяя эту нагрузку, снять показания всех приборов для:
а) нормального режима работы;
б) аварийного режима - обрыв линейного провода А (ключ К разомкнуть).
Обратить внимание, оказывает ли влияние на режимы других фаз и тока в линии изменение сопротивления фазы А.
5. Показания амперметров, вольтметра, ваттметров в пунктах 2 , 3 , 4 занести в таблицу 1.
6.На основании полученных данных рассчитать фазные значения активных мощностей по формулам:
РФАВ = UABIABcos
φAB,
РФВC= UBCIBCcosφBC , (7.14)
РФCA = UCA ICA cos φCA .
В формулах (7.14) для активной нагрузки cos φ = 1. Результаты занести в
табл.7-1.
-
По данным табл.1. построить векторные диаграммы для всех режимов работы.
Таблица.7-1.
| № пп. | Данные измерений | Данные вычислений | Характер нагрузки | ||||||||||||||
| IA | IB | IC | IAB | IBC | ICA | UAB | UBC | UCA | PW1 | PW2 | ∑PW | PФАВ | РФВС | РФСА | ∑РФ | ||
| A | A | A | A | A | A | B | B | B | Вт | Вт | Вт | Вт | Вт | Вт | Вт | ||
| | | | | | | | | | | | | | | | | | Симметричная нагрузка |
| | | | | | | | | | | | | | | | | | Обрыв лин. провода сим. нагрузка |
| | | | | | | | | | | | | | | | | | Несимметричная нагрузка |
| | | | | | | | | | | | | | | | | | Обрыв лин. Провода несим нагрузка |