ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.08.2024
Просмотров: 46
Скачиваний: 0
Интересно отметить, что из эмпирической зависимости, связывающей пробеги и энергию ядерной частицы, можно получить также оценку величины ионизационных потерь:
![]()
В качестве примера на Рис. б представлены рассчитанные с помощью этого соотношения линейные потери энергии при тех же условиях, что и для данных, представленных на Рис. а.
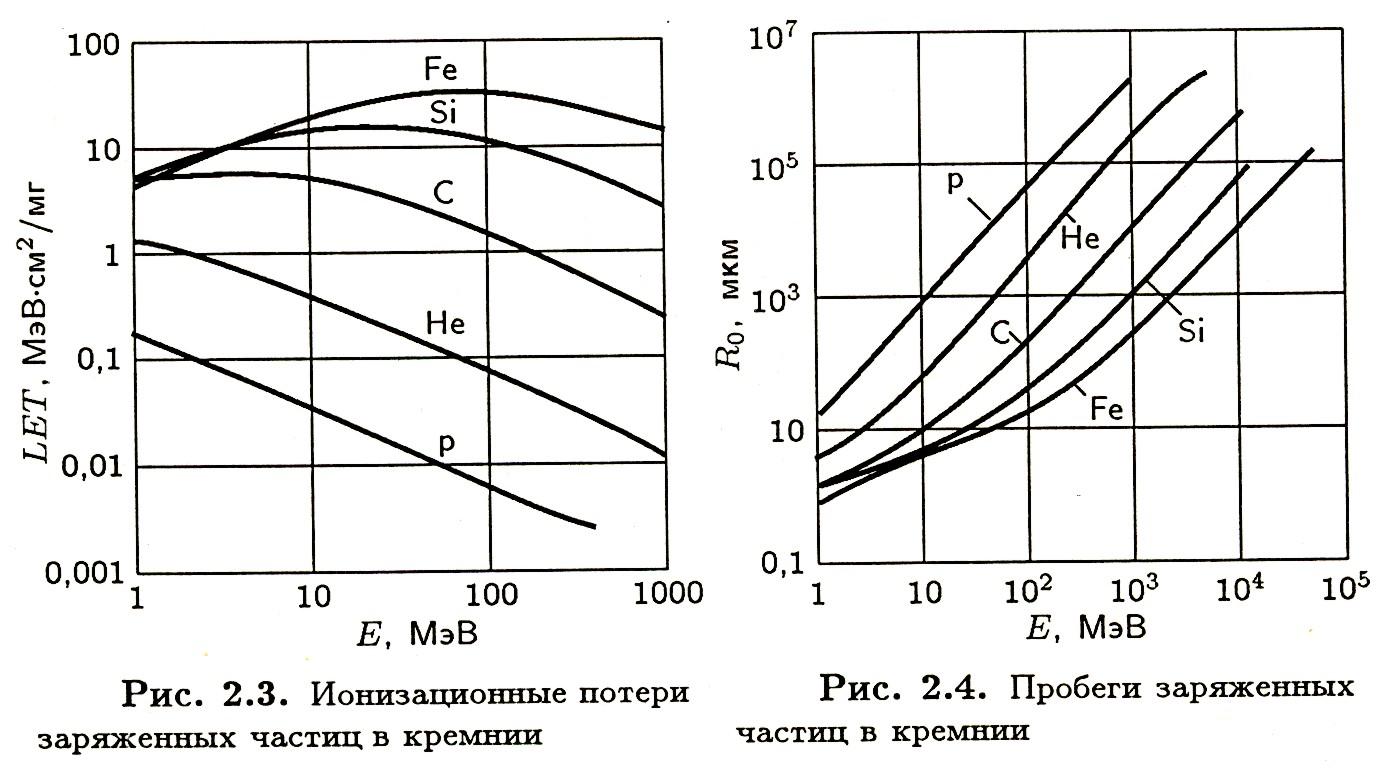
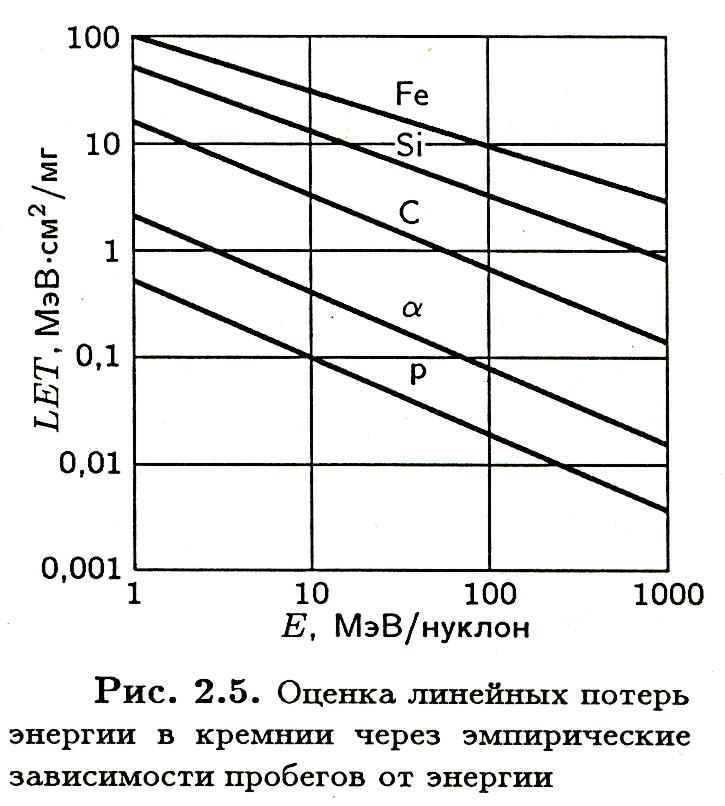
Рис. а. Ионизационные потери Рис.б. Оценка линейных потерь энергии
заряженных частиц в кремнии в кремнии через эмпирические зависимости
пробегов от энергии
Сравнение результатов показывает, что эмпирические соотношения дают очень большую погрешность при относительно малых энергиях и для относительно тяжелых ионов, поэтому пользоваться этими соотношениями можно только для относительно легких частиц и в области, где имеется монотонно-убывающая зависимость ЛПЭ от энергии частицы.
Рассматриваем пробеги альфа-частиц в воздухе.
Средний пробег Rв воздухе при комнатной температуре и нормальном давлении для альфа-частиц, испускаемых естественным изотопом, связан с энергией T(в МэВ) эмпирической формулой
R (см) = 0.32 (T)3/2
Пробеги альфа-частиц (см)
|
Вещество
|
Е = 4 МэВ |
Е = 6 МэВ |
Е = 8 МэВ |
Е = 10 МэВ |
|
Воздух
|
2.5 |
4.6 |
7.4 |
10.6 |
|
Биоткань
|
3.110-3 |
5.610-3 |
9.610-3 |
13.010-3 |
|
Алюминий
|
1.610-3 |
3.010-3 |
4.810-3 |
6.910-3 |
Пусть на слой поглотителя перпендикулярно к нему падает пучок однородных частиц с одинаковой энергией E0. Как будет выглядеть зависимость числа этих частиц N от толщины поглотителя x?
С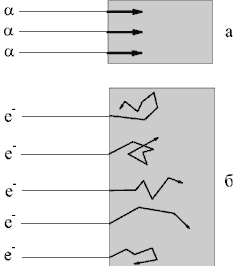 хематическое
представление поведения траекторий
первоначально параллельного пучка
нерелятивистских частиц в веществе. а
- альфа-частицы, б - электроны.
хематическое
представление поведения траекторий
первоначально параллельного пучка
нерелятивистских частиц в веществе. а
- альфа-частицы, б - электроны.
Характер движения электронов через вещество существенно иной, чем в случае тяжелых заряженных частиц. Траектория электронов прямолинейна только в начале пути. Среднеквадратичный угол многократного рассеяния нарастает как <θ2>1/2 ~ x 1/2. После большого числа актов рассеяния уже нельзя говорить о преимущественном направлении скоростей электронов – наступает режим диффузии. Наконец, в результате потерь энергии происходит полная остановка.
Для тяжелых заряженных частиц (практически всех частиц, кроме электронов), которые проходят слой поглотителя почти без рассеяния и поэтому имеют прямолинейную траекторию в веществе, все очень просто: частицы выбывают из пучка в основном из-за остановки в результате потерь энергии на ионизацию и возбуждение среды. А так как у них начальная энергия E0 была одинакова и средние потери энергии dE/dx тоже одинаковы, то все частицы должны были бы проходить одинаковые расстояния в веществе. В этом случае кривая поглощения должна описываться горизонтальной резко обрывающейся линией. На самом деле, вместо этой картины наблюдается
Разброс величины пробегов,
связанный со статистическим характером процесса ионизационных потерь. Частицы теряют свою энергию в очень большом, но конечном числе отдельных актов. Флуктуациям подвержено как число таких актов на единицу длины, так и потери энергии в каждом отдельном акте, в особенности в связи с образованием δ-электронов.
Пробеги отдельных частиц распределены около среднего пробега по закону Гаусса
![]() ,
,
где
![]() - средний пробег,
- средний пробег,![]() -
среднеквадратичное отклонение от
среднего значения
-
среднеквадратичное отклонение от
среднего значения

Относительный разброс пробегов
![]() называется стрэгглингом. Наличие этого
разброса приводит к тому, что кривая
поглощения имеет не резкий, а плавный
спад, такой, как изображен на рис. (для
α-частиц).
называется стрэгглингом. Наличие этого
разброса приводит к тому, что кривая
поглощения имеет не резкий, а плавный
спад, такой, как изображен на рис. (для
α-частиц).
В точке Rα
На основании свойств гауссова распределения можно найти, что интенсивность пучка упадет в два раза в точке x = Rα, которая соответствует среднему пробегу частиц. Более того, в этой точке кривая имеет наибольшую крутизну.
Построив касательную с максимальным наклоном в точке x=Rα и продолжив ее до пересечения с осью абсцисс, можно найти экстраполированный пробег Re . Обычно разность Re –Rα называется параметром разброса. Величина параметра разброса для тяжелых заряженных частиц не так велика и составляет единицы или десятые доли процента от Rα. Это обстоятельство дает возможность
по величине пробега с хорошей точностью определять энергию частиц.
Пробеги электронов.
Для электронов ситуация с пробегами иная. Понятие пробега для электронов весьма условно, потому что кроме ионизационных потерь для электронов существенную роль играют радиационные потери энергии. Кроме того, электроны испытывают в веществе многократное
рассеяние, и поэтому их путь в веществе не прямолинеен (как для тяжелых частиц). Направление их движения часто меняется, и только небольшое число электронов из пучка проходят максимальное расстояние в поглотителе в направлении, перпендикулярном к его поверхности.
Кривая поглощения коллимированного пучка моноэнергетических электронов имеет другой, чем для тяжелых частиц, вид:
Кривые поглощения электронов в Al
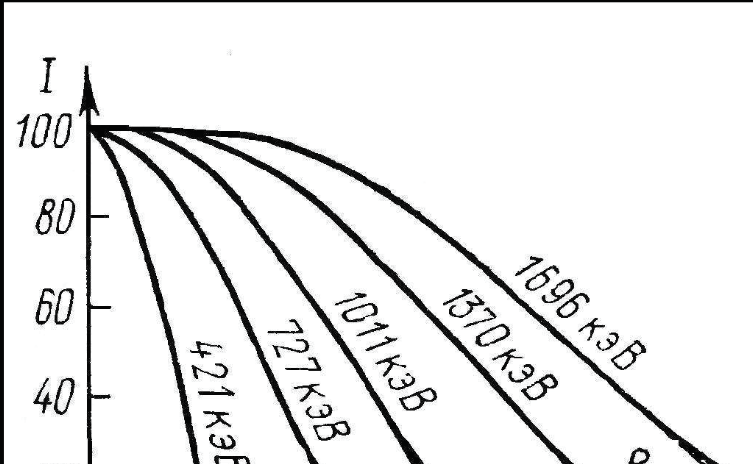
Рис. Зависимость изменения интенсивности I первоначально моноэнергетического пучка электронов от толщины алюминиевого поглотителя для разных энергий пучка;
Rэ - экстраполированный пробег для моноэнергетических электронов.
Относительный разброс пробегов (стрэгглинг) и параметр разброса для электронов значительно больше, чем для других частиц. Для электронов в качестве средней величины пробегов, как правило, используют экстраполированный пробег, т. е. такую толщину поглотителя, при которой продолжение линейно спадающего участка зависимости интенсивности электронного пучкаI(x)пересекает уровень нулевой интенсивности
Экстраполированные пробеги в г/см2 электронов с энергиейE(МэВ) в алюминии можно определить по формулам:
Rэ(Al)= 0.4×E1.4приЕ< 0.8 МэВ,Rэ(Al) = 0.54×Е - 0.133 приЕ > 0.8 МэВ.
Экстраполированный пробег электронов в веществе с зарядом Zи массовым числомАсвязан с пробегом в алюминии следующим образом:
Rэ(A,Z) = Rэ(Al)(Z/A)Al/(Z/A).
Экстраполированные пробеги электронов (см)
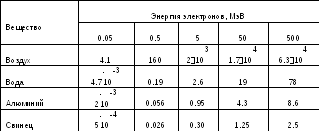
Максимальный пробег Rmax
Для электронов вводят еще одно понятие: максимальный пробег Rmax, это толщина вещества, в которой задерживаются все электроны. Теоретически рассчитать Rmax очень трудно. Поэтому для оценок обычно пользуются полуэмпирическими формулами. Например, для моноэнергетических электронов с энергией E (МэВ) часто
применяется простая формула:
![]() .
.
Обычно энергию электронов определяют не по пробегу, а по полной ионизации, произведенной ими в веществе.
δ-электроны
δ-электроны – это электроны высокой энергии (>> I), которые выбиваются из атомов в результате прохождения через вещество тяжелой заряженной частицы.δ-электроны ответственны за«волосатость»треков заряженных частиц, наблюдаемых в камере Вильсона или фотоэмульсиях.По числу δ-электронов, создаваемых частицами сверхвысоких энергий в космических лучах или от ускорителей, можно надежно судить о заряде этих частиц.
При столкновении заряженной частицы с электроном среды в случае достаточно малого параметра удара b~a электрон может получить такую энергию, что сам будет вызывать ионизацию других атомов. Такие электроны называютсяδ-электронами. При ионизационных потерях в каждом столкновении пролетающей частицы с электроном среды в среднем ею теряется очень небольшая порция энергии. И только в редких случаях передается значительная энергия, т.е. образуется δ-электрон.
Вспомним уже полученное нами соотношение между энергией электрона Те и параметром удара: (z – заряд частицы)
![]()