Файл: Лекция_2.doc

Задача 1.

Протон с энергией 100 МэВ пролетает на расстоянии b = 10^-10 cм от атома водорода.

Какую энергию потеряет протон? Способен ли в этом случае протон ионизовать атом водорода?

Задача 2.

Рассчитайте скорость протона, если его полная энергия равна 5 ГэВ.

Взаимодействие легких заряженных частиц со средой

Специфика:

• В силу малости массы, e^± движутся в веществе не по прямой и для них существенны радиационные потери энергии (на тормозное излучение).

• При столкновениях e^- с электронами вещества надо учитывать обменные эффекты. Обменное взаимодействие— взаимодействие тождественных частиц в квантовой механике, приводящее к зависимости значения энергии системы частиц от её полного спина . Представляет собой чисто квантовый эффект, исчезающий при предельном переходе к классической механике.

• В случае e⁺ возможен процесс его аннигиляции на электроне вещества (σ(e⁺+e^-→2γ) ~ 1/u).

Ионизационные потери легких заряженных частиц - электронов.

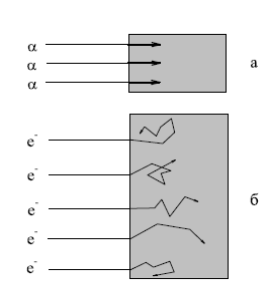
Прохождение электронов через вещество отличается от прохождения тяжёлых заряженных частиц. Главная причина - малая масса электрона. Это приводит к относительно большому изменению импульса электрона при каждом его столкновении с частицами среды, что вызывает заметное изменение направления движения электрона и как результат - электромагнитное радиационное излучение.     Удельные потери энергии электронов с кинетической энергией

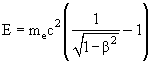
являются суммой ионизационных и радиационных потерь.

Ионизационные потери энергии электронами. В области низких энергий электронов (E < 1 МэВ) определяющий вклад в потери энергии дают неупругие ионизационные процессы взаимодействия с атомными электронами, включающие ионизацию атомов. Передаваемая в одном столкновении энергия в среднем очень мала и при движении в веществе потери складываются из очень большого числа таких малых потерь. Статистические флуктуации в ионизационных процессах ведут к разбросу потерь и величин пробегов.

---

В нерелятивистской области ионизационные потери быстро уменьшаются при увеличении энергии и достигают минимума при энергии E 1.5 МэВ, Рис. .

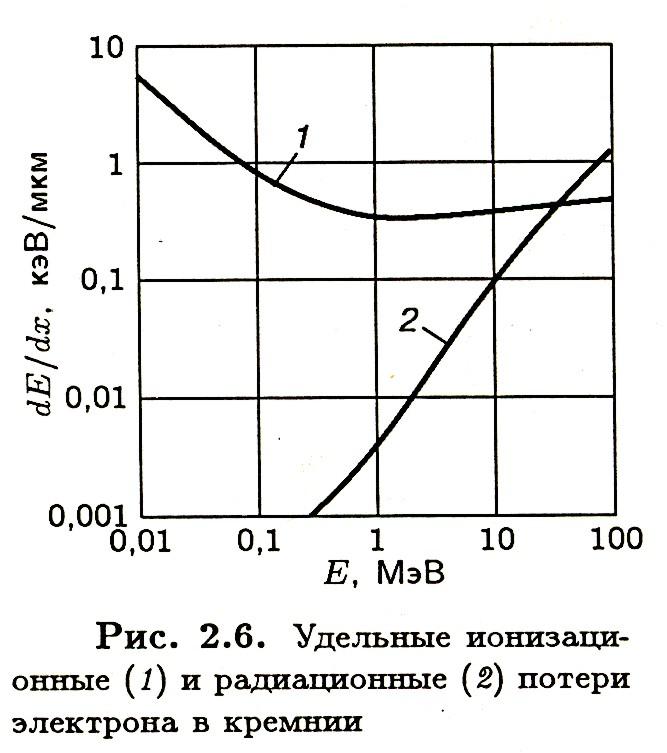
Рис. Удельные ионизационные (1) и радиационные (2) потери энергии электроном в кремнии

Далее потери очень медленно (логарифмически) растут с энергией, выходя на плато. Причиной такой зависимости является поляризация среды пролетающим электроном (эффект плотности). В результате ослабляется кулоновское поле релятивистского электрона, и в плотных средах (твёрдые тела, жидкости) потери не растут. В газах рост потерь может достигать нескольких десятков процентов.     При расчётах зависимости потерь учитывается

движение обоих электронов после взаимодействия и то, что

приведённая масса взаимодействующих электронов равна me/2.

Принимаются в расчёт также квантовомеханические эффекты тождественности электронов.

Относительная величина этих поправок составляет несколько процентов. Радиационные потери электронов (тормозное излучение подробно будет рассмотрено позднее).

Вывод формулы для потерь энергии на ионизацию электронами в принципе такой же, как и для других заряженных частиц. Также для электронов (z=1) получается соотношение:

Но величины bmin и bmax приходится выбирать по-другому.

Необходимо при этом учитывать, что

1) падающие электроны в процессе взаимодействия из-за малости

своей массы будут отклоняться от первоначального направления;

2) из-за тождественности взаимодействующих частиц будут возникать

обменные эффекты, имеющие квантовую природу.

При учете этих замечаний формула для удельных ионизационных

потерь электронов принимает вид:

.

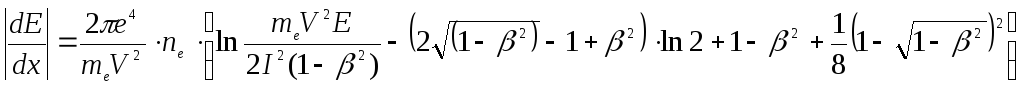В этой формуле - релятивистская кинетическая энергия электрона.

В нерелятивистскомслучае формула сводится к более простому выражению:

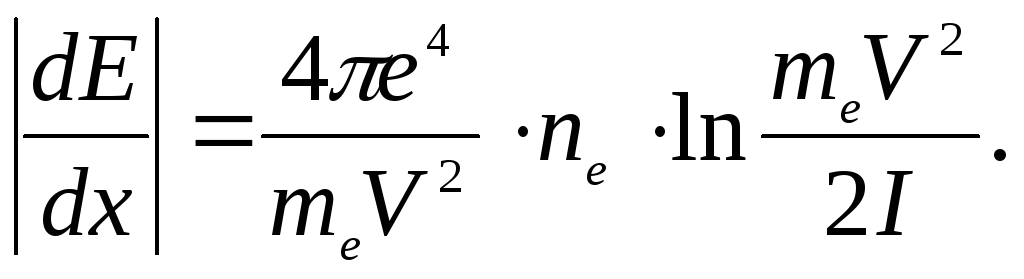
В ультрарелятивистскомслучае приE » mec² формула для потерь энергии также имеет простой вид:

---

В отличие от тяжелых частиц для электронов важны оба эти предельных случая, так как mec²=0,511 МэВ и электрон становится ультрарелятивистским уже при энергии в несколько МэВ.

Сравнение ионизационных потерь для электронов и тяжелых заряженных частиц приводит к следующим выводам.

1. Множители перед квадратными скобками в выражениях для ионизационных потерь электронов и тяжелых заряженных частиц одинаковы ( с точностью до множителя 2) , т.е. при одинаковых скоростях удельные потери их одинаковы ( с точностью до множителя 2).

Формула Бора

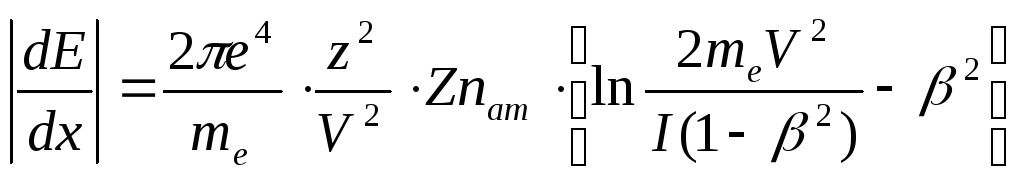
Формула Бете-Блоха для тяжелых заряженных частиц

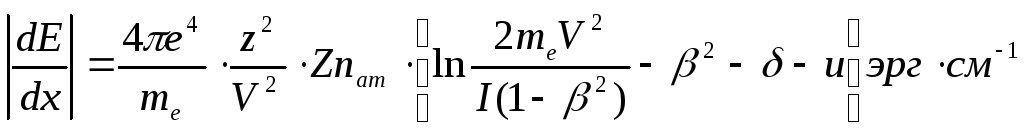
Для электронов

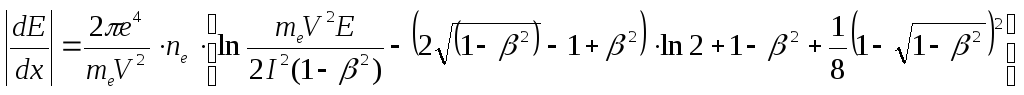
2. При одной и той же энергии электроновитяжелых частицв нерелятивистском случае удельные потери энергии пропорциональны массе частиц. Следовательно, для протонов они почти в 2000 раз больше, чем для электронов. Это очень важно для методов регистрации частиц. Например, в ядерных эмульсиях протоны с энергией 5 МэВ оставляют отчетливый след, тогда как электрон такой же энергии практически незаметен.

3. При очень высоких энергиях все по-другому. При V~c член перед скобкой не меняется. Становится существенной зависимость от 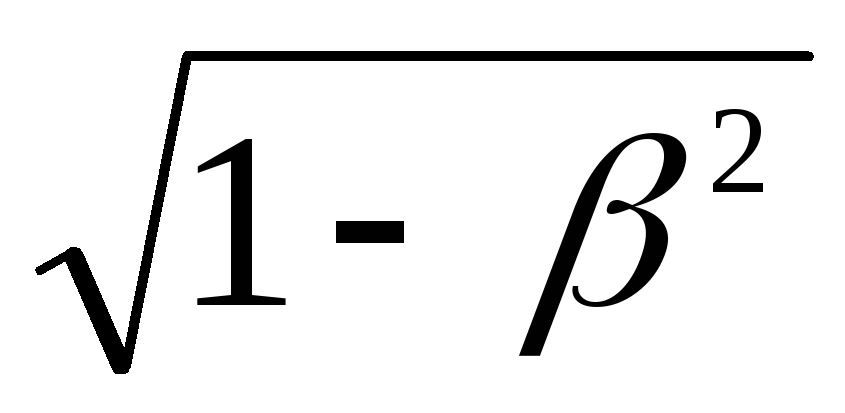под логарифмом. Поэтому при ультрарелятивистских скоростях величина dE/dx слабо зависит и от энергии, и от массы

частицы. Например, при кинетической энергии электрона и протона, равных 10 ГэВ потери энергии электронами в ≈ 2 раза превышают потери энергии протонами (при различии их масс в 2000 раз).

Пробег заряженных частиц в веществе

Потеряв всю энергию, частица останавливается. Расстояние, пройденное частицей в веществе, называется пробегом.На этом пути заряженная частица изменяет свою энергию от начального значения E0 до нуля в результате разных механизмов взаимодействия, основным из

которых для области энергий до 100 МэВ являются ионизационные потери. Поэтому понятно, что величина пробега зависит от массы, заряда, энергии частицы и характеристик среды.

---

Пробег R частицы с начальной энергией Е0 можно определить выражением

.

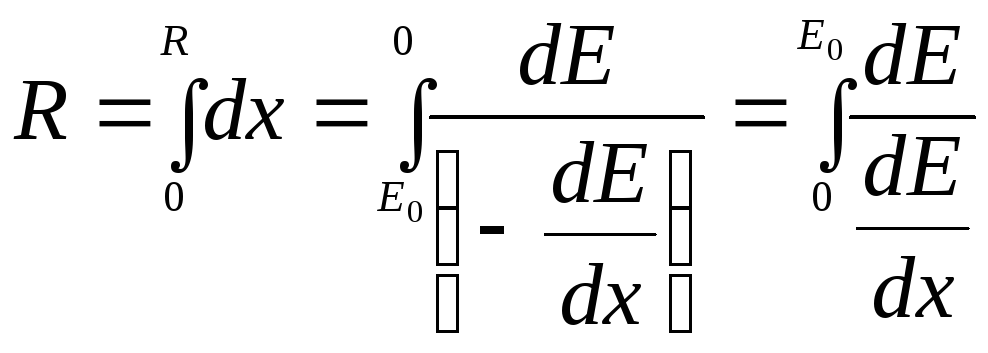
Подставим выражение для dEдля нерелятивистских частица из формулы Бете-Блоха

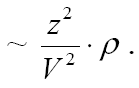
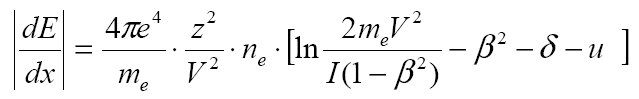
Оценим теперь, как пробег зависит от параметров частицы и среды:

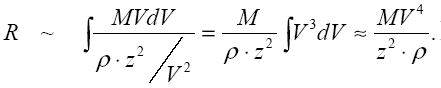
Выводы из этого соотношения:

1.При равных скоростях пробеги частиц прямо пропорциональны

их массам и обратно пропорциональны квадратам зарядов.

2.Пробеги обратно пропорциональны плотности среды, т.е. удобно измерять пробеги в массовых единицах длины. В этом случае величина пробега практически не будет зависеть от характеристик среды:

При более аккуратных расчетах не следует забывать, что в формуле Бете-Блоха есть еще коэффициенты, зависящие от среды: Z/AиI. Но для большинства веществ с малыми и средними A величина отношенияZ/A~0,5 и очень медленно падает с увеличением A, а средний ионизационный потенциалI стоит под знаком логарифма, т.е. тоже слабо влияет на величину средних потерь энергии и, как следствие этого, на величину пробега.

3.Чтобы сравнивать пробеги частиц с одинаковыми кинетическими энергиями, удобно несколько преобразовать выражение для R:

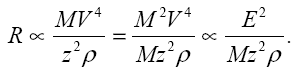
Из этого соотношения видно, что при равных кинетических энергиях пробеги частиц обратно пропорциональны их массам. Этот факт проиллюстрирован на Рис.

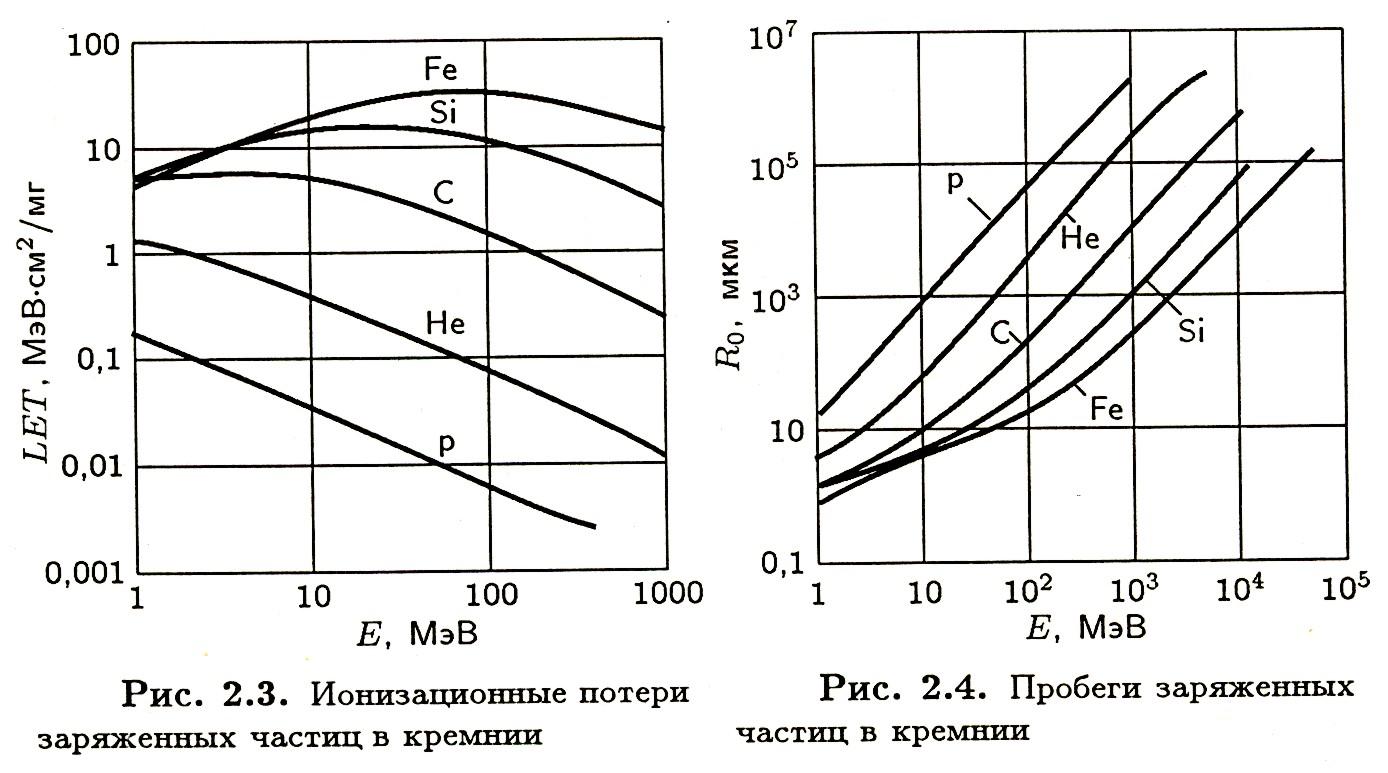
Рис. Ионизационные потери Пробеги заряженных

заряженных частиц в кремнии частиц в кремнии

Для сравнения рядом приведены графики ионизационных потерь.

---

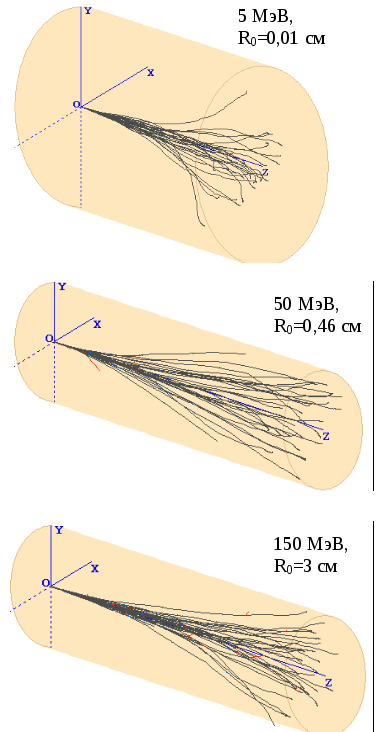
Траектории протонов в свинце.

Для практических целей

Для зависимостей R(Е) на основе обобщения экспериментальных данных и расчетов построены подробные таблицы и предложен ряд интерполяционных формул. На практике для оценок значений пробегов заряженных частиц используют приближенные эмпирические соотношения, справедливые в определенных интервалах энергии, вида

, гдепробег частицы с начальной энергиейЕ0, - эмпирический показатель степени порядка 1.5.

В таблице представлены коэффициенты аппроксимации для заряженных частиц в кремнии.

Коэффициент	р	-частица	С	Si	Fe
REo, мкм  Е0, МэВ	14.1 1.72 1	14.0 1.722 1	5.47 1.69 12	3.7 1.6 28	3.67 1.51 56

Заполняем таблицу Пробег, R(E), Е (МэВ)

	протон	-частица	Si1428	Fe5626
Энергия E= 1 МэВ
Энергия E= 10 МэВ
Энергия E= 100 МэВ
Энергия E= 500 МэВ
Энергия E= 1000 МэВ

---