Файл: Лекция_2.doc

Отсюда следует заключение, что большая передача энергии собразованием δ-электрона осуществляется при малых параметрах удара.

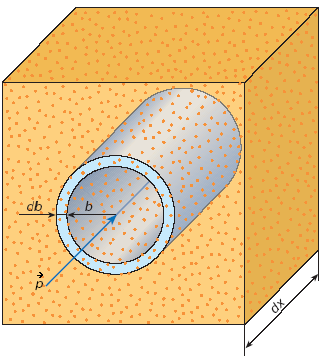
Фиксируем некий параметр удара bпри котором возможна большая передача энергииэлектронам среды с образованием δ-электронов в интервале энергий (Тe, Тe+dТe).

Поэтому вероятность образования δ-электронов определяется вероятностью оказаться электрону среды в кольце площадью 2πbdb около траектории частицы, т.е. dσδ = 2πbdb. Но

Cледовательно

При прохождении частицей пути dxона передает энергиюТeкаждому из электронов среды, находящихся в объеме кольцевого цилиндра радиусаb, с площадью кольца2πbdb и длинойdx . Объем такого кольцевого цилиндра – 2πbdbdx , а количество электронов, находящихся в нем –ne∙ 2πbdbdx, гдеne - плотность электронов в среде.

Таким образом, на единице своего пути в веществе частица образует

следующее число δ-электронов с энергией в интервале(Тe, Тe+dТe):

dNδ= 2πbdbdx ∙ ne=nedxdσδ.

Подставляем выражение для dσδ : .

Получаем:

, или,

Где (с учетом )

.

Таким образом, мы получили энергетический спектр δ-электронов :

из которого видно, что наиболее часто образуются δ-электроны малых энергий и по мере увеличения энергии δ–электронов число их резко падает.

Для релятивистских частиц  ≈1 величина Q перестает зависеть от энергии частицы:

---

,

а число δ-электронов с энергией Тe (МэВ) в интервале (Тe, Тe+dТe), созданных в среде на пути в 1 г/см² релятивистской частицей, получается равным:

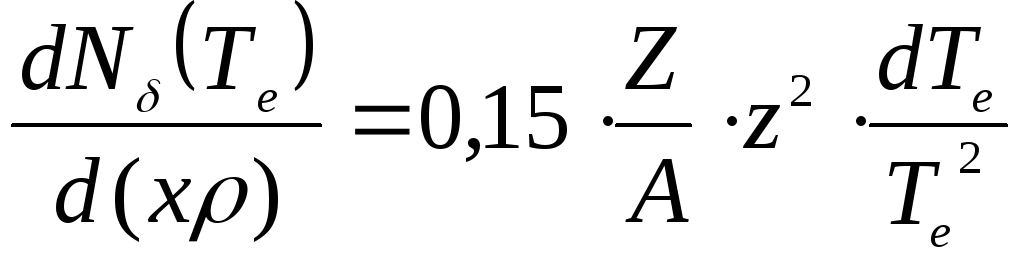
Из этой формулы видно, что число δ - электронов с энергией Тe, образованных в 1 г/см²вещества релятивистской частицей, прямо пропорционально квадрату заряда частицы z²и практически не зависит от характеристик среды, так как Z/A ≈ 0,5. Отсюда следует, что по плотности δ - электронов на треке частицы (например, в пузырьковой или фотоэмуль- сионной камере)можно определить заряд z релятивистской частицы.

Чтобы найти полное число δ-электронов на единице пути частицы(плотность δ-электронов), надо проинтегрировать по всем возможным энергиям δ-электронов Те от минимальной до максимальной:

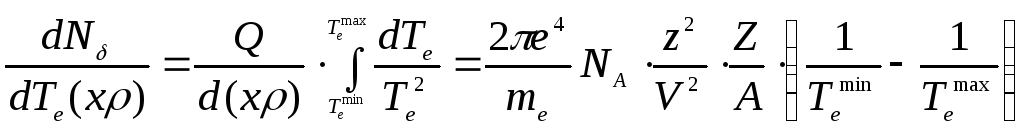
- некоторая нижняя граница δ-электронов, которая может быть выбрана довольно произвольно, но при условии, что δ- электроны все же могут сами ионизовать. Часто, например, принимают величину минимальной энергии

Максимальная энергия, которую может получить электрон при столкновении с ним частицы массы М и кинетической энергией Е, будет:

, и, еслиM>>me,.

Подставляя значения инайдем плотность-электронов на 1 г/см²пути:

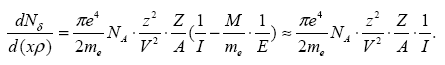
Трек ядра магния MgZ=12

Трек ядра серы S,Z=16

---

Трек ядра золота AuZ=79

Угловое распределение

Задача решается с точки зрения упругого рассеяния первичной частицы

на свободных электронах.

В системе центра инерции (СЦИ) угловое распределение δ-электронов определяется формулой Резерфорда:V– скорость налетющей частицы.

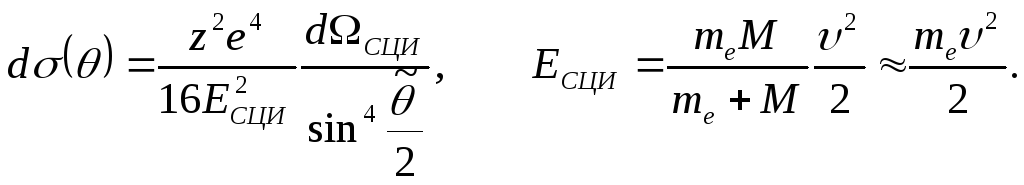
Преобразование этой формулы от интервала углов () к соответствующему интервалу углов в л.с. можно воспользоваться соотношениемψ = (π-)/2, где ψ – угол вылетаδ-электрона относительно направления движения частицы.

Эту формулу можно получить из векторной диаграммы импульсов и из законов сохранения энергии.

Отсюда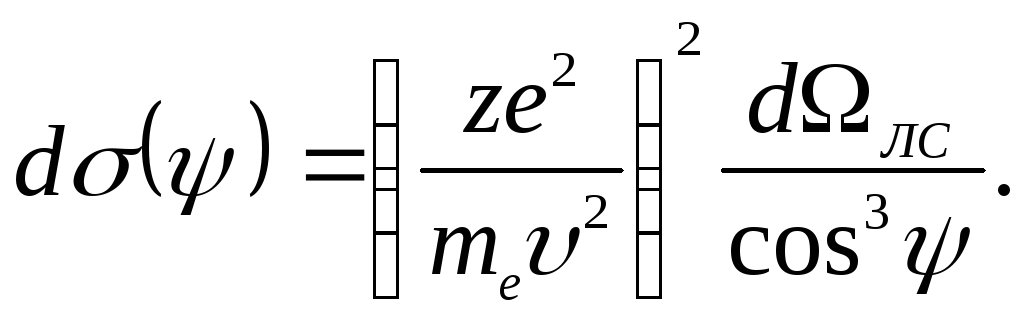

Преимущественное направление вылета δ-электроновψ ~ π/2. по отношению к направлению движения первичной частицы.

Энергия, переданная заряженной частицей δ – электрону,

связана с углом его вылета соотношением:

при M>>me/

Таким образом δ-электроны, вылетающие под малыми углами к траектории частицы

(ψ~0), имеют максимальную энергию,

а вылетающие под углами, близкими к π/2, имеют энергии минимальные. Зная

энергию δ – электрона (например, по пробегу) и угол его вылета ψ

можно оценить энергию частицы Е.

---