ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.09.2024
Просмотров: 47
Скачиваний: 0
СОДЕРЖАНИЕ
Молекулярная физика и термодинамика.
17. История атомистических учений. Наблюдения и опыты, подтверждающие
1. Все тела состоят из частиц – атомов и молекул.
2. Эти частицы находятся в непрерывном хаотическом (тепловом) движении
18. Идеальный газ. Давление газа. Основное уравнение мкт.
19. Тепловое движение. Абсолютная температура как мера средней кинетической
Абсолютная температурная шкала
20. Уравнение Клапейрона-Менделеева. Изопроцессы и их графики.
21. Объяснение агрегатных состояний вещества на основе атомно-молекулярных
22. Насыщенные и ненасыщенные пары. Влажность воздуха. Абсолютная и
23. Внутренняя энергия и работа газа. Первый закон термодинамики
Молекулярная физика и термодинамика.
17. История атомистических учений. Наблюдения и опыты, подтверждающие
атомно- молекулярное строение вещества. Масса и размеры молекул.
Постоянная Авогадро.
1. Все тела состоят из частиц – атомов и молекул.
Современные приборы(электронный микроскоп, ионный проектор) позволяют видеть отдельные атомы и молекулы.
2. Эти частицы находятся в непрерывном хаотическом (тепловом) движении
Опытные доказательства – диффузия и броуновское движение
Диффузия – взаимное проникновение молекул одного вещества в промежутки между молекулами другого вещества. Диффузию можно наблюдать для газообразных, жидких и твердых тел. Примеры:
Б роуновское
движение–тепловое движение
взвешенных в газе или жидкости частиц.
Обнаружил английский ботаник Роберт
Броун в 1827 году. Причина броуновского
движения частицы заключается в том, что
удары молекул жидкости о частицу не
компенсируют друг друга.
роуновское
движение–тепловое движение
взвешенных в газе или жидкости частиц.
Обнаружил английский ботаник Роберт
Броун в 1827 году. Причина броуновского
движения частицы заключается в том, что
удары молекул жидкости о частицу не
компенсируют друг друга.
Экспериментальное исследование броуновского движения – Жан Перрен.
Траектория броуновской частицы.
3. Частицы взаимодействуют друг с другом силами притяжения и отталкивания.
Опытные доказательства – существование твердых, жидких и газообразных тел; существование силы трения; усилие, необходимое для сжатия любого тела; существование объемных тел.
Масса и размер молекул. Постоянная Авогадро
Определения
m–масса всего вещества, кг
p–давление, Па
V-объем всего вещества, м3 . 1л= 10-3 м3
N– число всех молекул в веществе
ρ =m/V– плотность вещества, кг/м3. 1 г/см3 = 106 кг/м3
n=N/V– концентрация молекул, или число молекул в единице объема. 1/м3=м-3
m0–масса одной молекулы
Количество вещества ν(«ню»)пропорционально числу частиц.
Единица измерения количества вещества - моль
Моль равенколичеству вещества системы, содержащей столько же частиц, сколько содержится атомов в 0,012 кг углерода.
Постоянная Авогадро - количество молекул в одном моле вещества
![]()
Если известно количество вещества (число молей ν), то число молекул Nво всем веществе
![]()
Количество вещества можно найти как отношение числа атомов или молекул вещества к постоянной Авогадро:
![]()
Молярной массойназываетсявеличина, равная массе одного моля данного вещества:
![]()
Зная молярную массу, можно посчитать количество вещества:
![]()
Значения молярной массы, выраженные в г/моль, приведены в таблице Менделеева. Например, молярная масса атома водорода (H) равна1 г/моль,
молекулы водорода (H2)2 г/ моль,
молекулы углекислого газа (CO2 )12+32=44 г/моль,
молекулы воды (H2O)2+ 16=18 г/моль.
Масса молекул
Для определения массы одной молекулы m0нужноразделить массу вещества на число молекул в нем
![]()
Посчитаем массу одной молекулы воды:
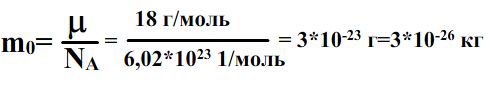
18. Идеальный газ. Давление газа. Основное уравнение мкт.
Д ля
объяснения свойств вещества в газообразном
состоянии вместо реального газа
используетсяего физическая модель -
идеальный газ.
ля
объяснения свойств вещества в газообразном
состоянии вместо реального газа
используетсяего физическая модель -
идеальный газ.
В модели идеального газа предполагается:
молекулы можно считать точечными массами;
между молекулами не действуют силы притяжения;
при соударении молекул друг с другом и со стенками сосуда действуют силы упругого отталкивания
Молекулы идеального газа обладают только кинетической энергией.
Основное уравнение МКТ позволяет вычислить давление газа, если известны масса молекулы, среднее значение квадрата скорости и концентрация молекул.
Давление идеального газа
Причина давления идеального газа на стенки сосуда заключается в том, что молекулы при столкновениях со стенками сосуда взаимодействуют с ними по законам механики как упругие тела.
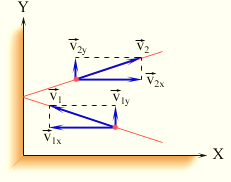 По
закону сохранения импульсав результате
упругого удара каждая молекула передает
стенке импульс, следовательно, на стенку
со стороны молекул действует сила.
По
закону сохранения импульсав результате
упругого удара каждая молекула передает
стенке импульс, следовательно, на стенку
со стороны молекул действует сила.
Если подсчитать импульс, переданный одной молекулой, умножить на число соударений и разделить на время наблюдения, мы получим давление газа на стенку сосуда.
Результат называется основным уравнение МКТ.
![]()
П![]() оскольку
среднее значение кинетической
энергии поступательного движения
молекул идеального газа:
оскольку
среднее значение кинетической
энергии поступательного движения
молекул идеального газа:
справедливо также уравнение
![]()
19. Тепловое движение. Абсолютная температура как мера средней кинетической
энергии частиц. Абсолютный нуль.Температура и ее измерение
Макроскопические параметры относятся к газу в целом – объем, давление, масса всего газа. Макроскопические параметры можно измерить с помощью приборов.
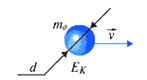
Микроскопические параметры – относятся к отдельным молекулам- масса одной молекулы, средняя скорость, средняя кинетическая энергия движения молекул, размер молекулы
Основное уравнение МКТ для идеального газа устанавливает связьмакроскопического параметра – давления – с микроскопическими параметрами газа - средняя кинетическая энергия и концентрация молекул.
Для того, чтобы узнать среднее значение кинетической энергии молекул или их концентрацию в отдельности, нужны измерения еще какой-то физической величины, связанной со средней кинетической энергией молекул. Такой величиной является температура.
Температураявляется мерой средней кинетической энергии движения молекул вещества.
Понятие температуры водится для состояния теплового равновесия.
Тепловое равновесие – это такое состояние, при котором все макроскопические параметры сколь угодно долго остаются неизменными.
Любое макроскопическое тело или группа макроскопических тел при неизменных внешних условиях самопроизвольно переходит в состояние теплового равновесия.
Температурахарактеризует состояние теплового равновесия системы тел: все тела системы, находящиеся друг с другом в тепловом равновесии, имеют одну и ту же температуру.
Для измерения температуры можно воспользоваться изменением любой макроскопической величины: объема, давления, электрического сопротивления и т.д.
Абсолютная температурная шкала
Более удобно измерять температуру в градусах. Абсолютная шкала называется также шкалой Кельвина.
Т![]() емпература,
измеренная по шкале Кельвина, связана
с температурой идеальной газовой шкалы
соотношением
емпература,
измеренная по шкале Кельвина, связана
с температурой идеальной газовой шкалы
соотношением
![]()
Коэффициент пропорциональности называетсяпостоянной Больцмана.
Из
определения величины
![]() следует, что
следует, что
![]()
Следовательно, температура, определяемая этой формулой, не может быть отрицательной. Наименьшим возможным значением температуры является0,если давление или объем равны нулю.
Предельную температуру, при которой давление идеального газа обращается в нуль при фиксированном объеме или объем идеального газа стремится к нулю при неизменном давлении, называют абсолютным нулем температуры.
Нулевая температура по шкале Кельвина соответствует абсолютному нулю, а каждая единица температуры по этой шкале равна градусу по шкале Цельсия.
Единица температуры по шкале Кельвина (один Кельвин, К) равна одному градусу Цельсия:
1 К = 1 0С
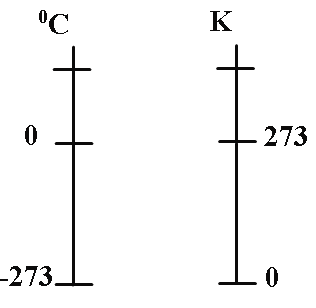
Значения температуры, измеренные по шкалам Кельвина и Цельсия, связаны соотношением
TK=tC+273
Уравнение можно записать иначе:
Поскольку N/V= n (концентрация молекул), получаем
![]()
И![]() з
уравнения
з
уравнения
![]()
получаем
Среднее значение квадрата скорости молекул
![]()
20. Уравнение Клапейрона-Менделеева. Изопроцессы и их графики.
Уравнение состояние идеального газа связывает между собой основные макроскопические параметры –давление, объем и температуру.
Запишем основное уравнение идеального газа
![]()
Выразим концентрацию молекул через объем газа
![]()
Выразим число молекул через количество вещества
![]()
Подставим результат в выражение для концентрации молекул