Добавлен: 21.10.2018
Просмотров: 1120
Скачиваний: 19
СОДЕРЖАНИЕ
Задание 2. Числовые характеристики симметричной квадратной матрицы.
Задание 3. Формула Тейлора для функции нескольких переменных
Задание 4. Нахождение локальных экстремумов
Задание 5. Одномерная оптимизация
Задание 6. Многомерная оптимизация по направлению
Задание 7. Методы безусловной оптимизации
Задание 8. Методы условной оптимизации
Задание 9. Задача линейного программирования и симплекс-метод
Задание 10. Транспортная задача
Задание 1. Линии уровня
1.1. Приведите определение и свойства линии уровня функции нескольких переменных.
1.2. Укажите связь между линиями уровня и градиентами.
1.3. Постройте линии уровня Uα для функции
y = -9*x1 + 29*x2
при α=0, α=1, α=2.
1.4. Постройте линию уровня Uα при α=3 для функции
y = x1^2 –9*x1*x2 +2*x2^2 + 9*x1.
Вычислите и нарисуйте градиент этой функции в точке (1; 1).
Задание 2. Числовые характеристики симметричной квадратной матрицы.
2.1. Приведите определения и геометрическую интерпретацию числовых характеристик квадратной матрицы:
-
определитель,
-
число обусловленности,
-
собственные числа,
-
собственные векторы,
-
сингулярные числа.
2.2. Найдите гессиан H функции f(x, y) = 9x^2 +4xy+5y^2 в точке (1; 0).
Постройте множество точек, в которое оператор с матрицей H отображает единичную окружность S1 с центром в точке (0; 0). Этот образ является эллипсом. Полуоси являются собственными векторами матрицы H, а длины полуосей – собственными числами i.
2.3. Постройте линию уровня Uα=1 функции f(x, y) в точке (1, 0). Линия уровня также является эллипсом, полуоси которого – собственные векторы, а длин полуосей являются сингулярными числами матрицы и обратно пропорциональны квадратному корню из соответствующего собственного числа, то есть равны 1/i0,5. В некотором смысле, два эллипса из пунктов 5.2 и 5.3 являются ортогональными и взаимно-обратными.
Задание 3. Формула Тейлора для функции нескольких переменных
3.1. Приведите формулу Тейлора для функций одной и нескольких переменных
3.2. Проведите квадратичную аппроксимацию в точке (1; 1) для функции
F(x, y) = (x + y - 9) e – (x^2 – xy + y^2)
Задание 4. Нахождение локальных экстремумов
4.1. Используя критерии оптимальности, найдите экстремумы для функции
F(x, y) = (x + y - 9) e – (x^2 – xy + y^2)
4.2. Проверьте правильность нахождения точек экстремума двумя свойствами:
-
с помощью графика этой функции,
-
путем случайного перебора точек в малой окрестности точки локального экстремума.
Задание 5. Одномерная оптимизация
Найти точки экстремума функции
F(x) = x6 – 9x5 + 9x3 – 10x2 + x.
Задание 6. Многомерная оптимизация по направлению
Найти точку локального минимума функции
F(x) = x12 +9x22 + x32 +3x1x2 – 9x1x3 – x2x3 + x1 – 9x2 + x3
Задание 7. Методы безусловной оптимизации
-
Аналитически найти стационарные точки заданной функции, области выпуклости/вогнутости функции. Найти точку глобального минимума. Оценить «овражность» исследуемой функции в окрестности точки минимума.
-
Построить график функции, используя средства EXCEL или MATLAB.
-
Решить задачу минимизации численным методом из нескольких начальных точек. Сделать вывод об эффективности выбранного метода.
-
При выполнении задания на языке СИ написать классы для работы с векторами и матрицами.
Задание выбирать в соответствии с порядковым номером фамилии студента в списке группы.
-
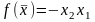 exp[1-
exp[1-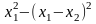 ],
метод
сопряженных
направлений.
],
метод
сопряженных
направлений.
Контрольные вопросы
Объяснить алгоритмы следующих методов
-
Метод конфигураций (Хука-Дживса).
-
Метод деформируемого многогранника (Нелдера Мида).
-
Метод наискорейшего спуска.
-
Метод сопряженных направлений и его модификации.
-
Метод Ньютона и его модификации.
-
Метод дробления шага.
Задание 8. Методы условной оптимизации
-
Решить задачу минимизации функции методом множителей Лагранжа.
-
Решить ЗНП методом седловой точки. Промежуточную задачу решения СЛАУ решить, используя EXCEL.
-
Решить задачу численным методом [8]. Метод условной минимизации выбрать самостоятельно (см. 1.4.-1.6). Сравнить результат с теоретическим решением.
Задания выбирать в соответствии с порядковым номером студента в журнале.
1.
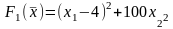 ,
,
Ограничения (для всех вариантов):
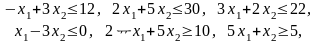
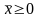 .
.
Контрольные вопросы
-
Активные и пассивные ограничения. Регулярная задача.
-
Теорема Куна-Такера.
-
Достаточные условия минимума в задачах математического программирования.
-
Седловая точка.
-
Метод седловой точки для задачи квадратичного программирования.
Задание 9. Задача линейного программирования и симплекс-метод
Вариант 1. Для изготовления четырёх видов продукции (А, Б, В и Г) используется три вида сырья (I, II и III). Ресурсы сырья, нормы его расхода на единицу продукции и получаемая прибыль от единицы продукции заданы в следующей таблице:
|
Сырьё |
Нормы расхода |
Ресурсы Б |
||||
|
А |
Б |
В |
А |
|||
|
I |
2 |
1 |
I |
2 |
1 |
|
|
II |
1 |
5 |
II |
1 |
5 |
|
|
III |
3 |
0 |
III |
3 |
0 |
|
|
Прибыль |
7,5 |
3 |
Прибыль |
7,5 |
3 |
|
Определить оптимальный план выпуска продукции из условия максимизации прибыли.
Задание 10. Транспортная задача
Решить транспортные задачи, заданные матрицами перевозок
|
Вар.1 |
|
В1 |
В2 |
В3 |
В4 |
В5 |
В6 |
В7 |
|
|
|
115 |
200 |
60 |
40 |
75 |
50 |
120 |
|
А1 |
240 |
2 |
М |
8 |
11 |
3 |
1 |
5 |
|
А2 |
180 |
7 |
4 |
3 |
12 |
5 |
9 |
М |
|
А3 |
90 |
1 |
10 |
5 |
1 |
4 |
6 |
2 |
|
А4 |
45 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
|
А5 |
100 |
9 |
6 |
5 |
3 |
2 |
1 |
5 |
Литература
-
Стандарт предприятия: Общие требования и правила оформления дипломных и курсовых проектов (работ). СТП УГТУ-УПИ 1-96. Екатеринбург, 1996.
-
Акулич И.Л. Математическое программирование в примерах и задачах. – М.; Высшая школа, 1993. – 335 с.
-
Аттетков А.В., Галкин С.В., Зарубин В.С. Методы оптимизации - М.; Издательство МГТУ им. Н.Э. Баумана, 2004. - 432 с
-
Васильев В.П. Численные методы решения экстремальных задач. - М.: Наука, 1980. - 518 с.
-
Габбасов Р., Кириллова Ф.М. Методы оптимизации. – Минск: Изд-во БГУ, 1981. -
-
Дьяконов В. Matlab: учебный курс / В. Дьяконов. СПб.: Питер, 2001. 560 с.
-
Пантелеев А.В., Летова Т.А. Методы оптимизации в примерах и задачах. – М.; Высшая школа, 2005. – 544 с.
-
Васин В.В., Еремин И.И. Операторы и итерационные процессы фейеровского типа (теория и приложения). Москва-Ижевск: Институт компьютерных исследований, НИЦ «Регулярная и хаотическая динамика», 2005. – 200 с.
-
Визильтер Ю.В., Горбацевич В.С. Описание формы объектов на изображениях при помощи гибких структурирующих элементов // Сборник трудов научно-технической конференции «Техническое зрение в системах управления 2011». М.: ИКИ РАН. 2011. С. 162-167.
-
Горбацевич В.В. Современное линейное программирование (Сборник задач с решениями на MAPLE5). М.: 1999 – 34 с.
-
Калихман И.Л. Сборник задач по математическому программированию. Изд. 2-е доп. и перераб. М., «Высш. школа», 1975. 270 с. с ил.
-
Схрейвер А. Теория линейного и целочисленного программирования: В 2-х т. Т. 1: Пер. с англ. – М.: Мир, 1991. – 360 с., ил.
-
Филатов А.Ю. Развитие алгоритмов внутренних точек и их приложение к системам неравенств: Автореф. дис. ... канд. физ.-матем. наук. Иркутск, 2001. 19 с.
Приложение. Рекомендации по использованию EXCEL и MATLAB
П1. Построение графиков
Для построения графика функции y=f(x1,x2) могут быть использованы следующие инструменты:
-
В EXCEL – Мастер диаграмм, подтип Поверхность.
-
Используя автозаполнение, на листе EXCEL в столбец А и первую строку с выбранным шагом ввести соответственно значения переменных x1 и x2, для которых будут вычисляться значения функции.
-
В ячейку В2 ввести выражение для вычисления функции f(x1,x2) в точках $A2, B$1 (знак $ - признак абсолютной адресации, при которой будут зафиксированы первый столбец– перебор значений переменной x1 и первая строка – перебор значений переменной x2) и нажать одновременно три клавиши Ctrl, Shift, Enter, поскольку формула используется для обработки массивов. В строке формул должны появиться фигурные скобки.
-
Выделить ячейку В2 и, протянув маркер заполнения сначала вниз, пробегая все ячейки, заполненные в столбце А. а затем вправо, пробегая все ячейки, заполненные в строке 1, заполнить массив значений функции в узловых точках области построения графика.
-
На вкладке Стандартные Мастера диаграмм выбрать Поверхность. Поверхностная диаграмма дает 3-мерное изображение функции, а Контурная диаграмма представляет вид сверху на поверхностную диаграмму и является аналогом линий уровня исследуемой функции.
В MATLAB – функции plot3, mesh, surf, surfl.
-
С помощью функции meshgrid получить двумерные массивы координат узловых точек области построения графика: u=a:∆1:b; v=c: ∆2:d; [x,y]=meshgrid(u,v);
-
Задать исследуемую функцию: f= f(х,у);
-
Применяя указанные выше функции, получить трехмерное изображение: plot3(x,y,f) или mesh(x,y,f), surf(x,y,f), surfl(x,y,f).
П2. Действия с матрицами
Для нахождения собственных значений и собственных векторов матрицы Гессе могут быть использованы следующие инструменты MATLAB
-
λ = eig(a) - функция eig(a) возвращает собственные значения заданной матрицы a. Пример задания матрицы 4х4: a = [16 3 2 13; 5 10 11 8; 9 6 7 12; 4 15 14 1] .
-
[v,d] = eig(a) – при таком обращении функция возвращает собственные векторы v и собственные значения как элементы диагональной матрицы d.
Для нахождения матрицы, обратной матрице Гессе могут быть использованы следующие инструменты:
1. В EXCEL – функция МОБР возвращает обратную матрицу для матрицы, хранящейся в массиве.
2. В MATLAB – функция y=inv(a) возвращает обратную матрицу для матрицы a.