Добавлен: 04.04.2023
Просмотров: 99
Скачиваний: 2
СОДЕРЖАНИЕ
1 ИСТОРИЯ РАЗВИТИЯ ЯЗЫКОВ ПРОГРАММИРОВАНИЯ
1.1 Эволюция вычислительной техники
1.2 Эволюция языков программирования
2 ОСНОВНЫЕ АЛГОРИТМИЧЕСКИЕ СТРУКТУРЫ
2.1 Общие принципы построения алгоритмов
3 РАЗРАБОТКА ПРОГРАММ НА ЯЗЫКЕ ПРОГРАММИРОВАНИЯ QBASIC
3.1 Разработка программ с использованием оператора цикла
В роли исполнителей могут выступать человек, компьютер, робот-манипулятор, станок с программным управлением (рисунок 9).
Выделяют следующие свойства алгоритма:
1. Детерминированность - обеспечение определенности и однозначности результата выполнения алгоритма при заданных исходных условиях.
2. Дискретность – любой алгоритм может быть представлен в виде отдельных элементарных действий, которые могут быть выполнены исполнителем.
3. Массовость означает, что алгоритм может решать задачи одного типа при разных исходных условиях.
4. Результативность (конечность) – при корректно заданных исходных условиях выполнение алгоритма должно закончиться получением искомого результата за конечное время.

Рисунок 9 – Исполнители алгоритмов
Существует несколько общепринятых способов описания алгоритмов:
- словесный;
- с помощью блок-схем (графический способ);
- на алгоритмическом языке;
- с помощью языка программирования.[8]
Словесный способ записи алгоритмов предполагает описание алгоритма на естественном человеческом языке. Пример такой формы записи алгоритма представлен на рисунке 10.
Словесный способ не получил широкого распространения, так как словесные описания:
- не являются строго формализуемыми;
- обычно избыточны;
- могут содержать неоднозначные инструкции.
Рисунок 10 – Словесное описание алгоритма
Чаще всего при проектировании алгоритмов используют графическое изображение алгоритма в виде блок-схемы, когда каждому действию соответствует определенный блок (геометрическая фигура).[19] Пример алгоритма в форме блок-схемы представлен на рисунке 11.
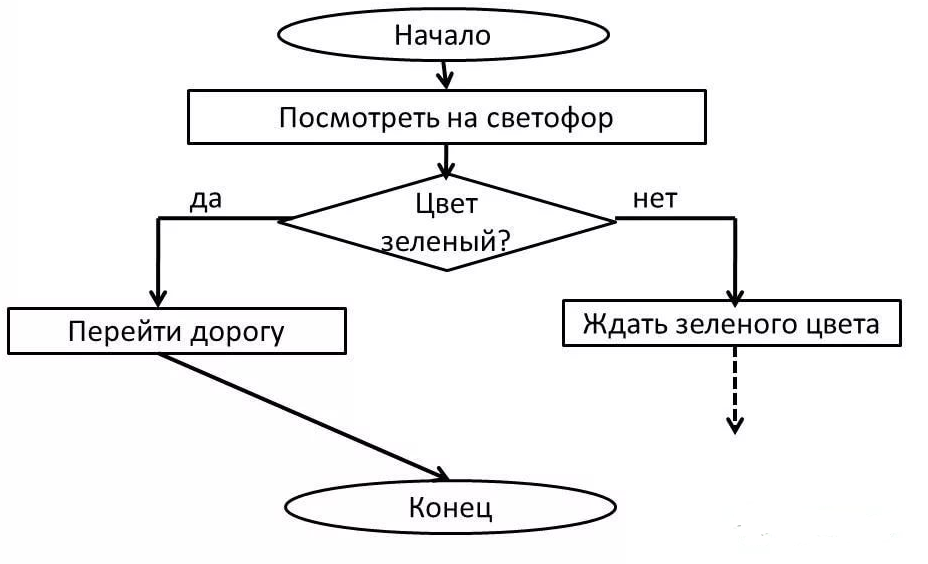
Рисунок 11 – Блок-схема алгоритма перехода дороги
Алгоритмический язык представляет собой искусственный язык псевдокодов. Пример представлен на рисунке 12.
Рисунок 12 – Алгоритм решения квадратного уравнения на алгоритмическом языке
Любой корректно составленный алгоритм, записанный одним из перечисленных способом, может быть представлен в виде программы для компьютера.
При формировании алгоритмов рекомендовано применять следующие основные принципы.
- Принцип поэтапной детализации алгоритма (иначе этот принцип называют «проектирование сверху вниз»). При реализации этого принципа алгоритм первоначально разрабатывают в форме укрупненных блоков (разбиение задачи на подзадачи), а затем выполняют постепенную детализацию этих блоков.
- Принцип разработки «от главного к второстепенному», который предполагает составление алгоритма, начиная с главной конструкции. При реализации этого принципа иногда достраивают алгоритм в обратном направлении, например, от конца к середине.
- Принцип структурирования, который декларирует использование в программе только типовых алгоритмических структур при разработке алгоритма. При использовании в алгоритме нетиповых структур (например, цикл с дополнительными выходами из цикла в теле цикла или злоупотребление безусловного перехода) существенно осложняет чтение и отладку алгоритма.[10]
Основными алгоритмическим структурами являются:
- следование (линейный алгоритм);
- ветвление (разветвляющийся алгоритм);
- цикл (циклический алгоритм).
Грамотно разработанный алгоритм, как правило, состоит из комбинации основных алгоритмических структур.[15]
Наглядно представить, как работает та или иная алгоритмическая структура, можно на примере графических операторов.
2.1 Следование
Следование – определяет линейную последовательность действий. Каждый блок при этом может содержать как простые операторы, так и сложную структуру. Блок должен строго иметь один вход и один выход.[6]
Блок-схема линейной алгоритмической структуры представлена на рисунке 13.
Рисунок 13 – Следование
Пример реализации линейной алгоритмической конструкции представлен в таблице 1.
Таблица 1 – Пример реализации следования
|
Программа на QBasic |
Результат выполнения программы |
|
CLS SCREEN 7 CIRCLE (20, 20), 15, 14 LINE (50, 50)-(100, 75), 3, BF CIRCLE (120, 130), 70, 12, , , .3 PAINT (120, 130), 5, 12 |
|
В данном примере последовательно выполняются согласно алгоритму следующие действия:
- строится окружность желтого цвета;
- строится голубой закрашенный прямоугольник;
- строится эллипс красного цвета;
- внутренняя область эллипса заливается сиреневой заливкой.
2.2 Ветвление
Ветвление является реализацией альтернативы. В ходе выполнения программы управление передается одному из двух блоков в зависимости от истинности или ложности заданного условия. После выполнения одного из блоков происходит выход из ветвления, и программа продолжает выполнение.[3]
Ветвление может быть реализовано как в полной форме (когда присутствуют действия и в случае выполнения условия, и в случае невыполнения) и в краткой форме (в этом случае действие выполняется только в случае выполнения условия).[9]
На рисунках 14 и 15 представлены блок-схемы полной и краткой форм ветвления.
Рисунок 14 – Полная форма ветвления
Рисунок 15 – Краткая форма ветвления
Пример реализации разветвляющейся алгоритмической конструкции представлен в таблице 2.
Таблица 2 – Примеры реализации ветвления
|
Программа на QBasic |
Результат выполнения программы |
|---|---|
|
CLS SCREEN 7 INPUT "Vvedite 1 ili 2"; N IF N = 1 THEN CIRCLE (160, 90), 50, 1 ELSE LINE (120, 70)-(200, 110), 6, B END IF |
|
|
CLS SCREEN 7 INPUT "Vvedite 1 ili 2"; N IF N = 1 THEN CIRCLE (160, 90), 50, 1 ELSE LINE (120, 70)-(200, 110), 6, B END IF |
|
|
CLS SCREEN 7 INPUT " a = "; a IF a MOD 2 = 0 THEN CIRCLE (160, 90), 50, 1 PAINT (160, 90), 14, 1 END IF |
|
В первых двух строках таблицы показаны результаты выполнения оператора условного перехода в полной форме: если пользователь ввел число 1, то программа рисует окружность, если число 2 – программа выводит прямоугольник.
В последней строке таблицы – результат выполнения краткой формы оператора условного перехода. При вводе пользователем четного числа программа рисует и закрашивает окружность, при вводе нечетного числа никаких действий не производится.
2.3 Цикл
Цикл реализовывает повторение некоторой группы действий (тело цикла) при разных значениях переменной цикла. Закон изменения переменной цикла задается параметрами цикла.[11]
Различают несколько видов циклического алгоритма. В QBasic реализованы три из них – итерационный цикл, цикл с предусловием и цикл с постусловием (блок-схемы представлены на рисунках 16 – 17).
Рисунок 16 – Блок-схема итерационного цикла
А – начальное значение переменной цикла, В – конечное значение переменной цикла, step – шаг цикла.
|
Цикл с предусловием |
Цикл с постусловием |
|
|
|
Рисунок 17 – Блок-схемы цикла с постусловием и цикла с предусловием
Пример реализации разветвляющейся алгоритмической конструкции представлен в таблице 3.
Таблица 3 – Примеры реализации циклов
|
Программа на QBasic |
Результат выполнения программы |
|---|---|
|
Итерационный цикл CLS SCREEN 7 RANDOMIZE TIMER FOR i = 1 TO 10 CIRCLE (160, 90), i * 10, RND * 15 + 1 NEXT i |
|
|
Цикл с предусловием CLS SCREEN 7 RANDOMIZE TIMER x = 10 WHILE x < 200 LINE (x + 10, 50)-(x + 30, 80), RND * 15 + 1, B x = x + 30 WEND |
|
|
Цикл с постусловием CLS SCREEN 7 RANDOMIZE TIMER x = 10: y = 10 DO CIRCLE (x, y), RND * 15 + 1, RND * 20 + 10 x = x + 20: y = y + 20 LOOP UNTIL (x >= 220 OR y >= 120) |
|
3 РАЗРАБОТКА ПРОГРАММ НА ЯЗЫКЕ ПРОГРАММИРОВАНИЯ QBASIC
3.1 Разработка программ с использованием оператора цикла
Принцип работы оператора цикла можно хорошо понять, выполняя программы с использованием графики и внося изменения в параметры цикла.
Ниже представлены три программы – первая базовая, результатом выполнения которой являются окружности малого радиуса, размещенные на окружности большого радиуса.
Две следующие программы являются модификациями первой программы – в обе добавлен еще один цикл (то есть использованы вложенные циклы – схема представлена на рисунке 18, а). [18]
Рисунок 18 – Допустимая (а, б) и недопустимая (в) схемы использования нескольких циклов в программе
Код программы, рисующей окружности малого радиуса на окружности большего радиуса (okr1.bas)
R = 120
R1 = 10
N = 20
SCREEN 12
CIRCLE (320, 240), R,4
P = 2 * 3.14 / N
FOR I = 1 TO N
X = COS(P * I) * R
Y = SIN(P * I) * R
CIRCLE (320 + X, 240 + Y), R1,14
NEXT I
Результат выполнения программы представлен на рисунке 19.
Рисунок 19 – Результат выполнения программы okr1.bas
В программе R – радиус большой окружности, R1 – радиус маленьких окружностей, N – их количество.
Параметры цикла:
- начальное значение переменной цикла 1;
- конечное значение переменной цикла N (20);
- шаг цикла не указан (step отсутствует), по умолчанию он равен 1.
Так как в программе окружности нарисованы контрастными цветами – большая красным цветом, маленькие – желтым, то при добавлении внешнего цикла и изменении параметров будет понятно, за какие изменения отвечают определенные параметры.
В следующей программе в коде базовой программы добавлен внешний цикл, рисующий большие окружности переменного радиуса. Внутренний цикл оставлен без изменений.
Код программы okr2.bas
R = 120
R1 = 10
N = 20
SCREEN 12
FOR R = 120 TO 20 STEP -20
CIRCLE (320, 240), R, 4
P = 2 * 3.14 / N
FOR I = 1 TO N
X = COS(P * I) * R
Y = SIN(P * I) * R
CIRCLE (320 + X, 240 + Y), R1, 14
NEXT I
NEXT R
Внешний цикл регламентирует изменение радиуса большой окружности.
Параметры внешнего цикла:
- начальное значение переменной цикла 120;
- конечное значение переменной цикла 20;
- шаг цикла 20.
Цикл является убывающим, так как переменная цикла изменяется от большего значения к меньшему значению с отрицательным шагом.[7]
Результат выполнения программы представлен на рисунке 20.
Рисунок 20 – Результат выполнения программы okr2.bas
На рисунке видно, что на каждой окружности красного цвета (радиус этих окружностей циклически меняется) размещены 20 окружностей радиуса 10 желтого цвета.
В следующей программе во внешнем цикле изменяются радиусы желтых окружностей, в радиус красной остается неизменным.
Код программы okr2.bas
R = 120
R1 = 10
N = 20
SCREEN 12
FOR R1 = 60 TO 120 STEP 20
CIRCLE (320, 240), R, 4
P = 2 * 3.14 / N
FOR I = 1 TO N
X = COS(P * I) * R
Y = SIN(P * I) * R
CIRCLE (320 + X, 240 + Y), R1, 14
NEXT I
NEXT R1
Результат выполнения программы представлен на рисунке 21.
Рисунок 21 – Результат выполнения программы okr3.bas
На рисунке видна единственная красная окружность и множество желтых окружностей различного радиуса.
3.2 Разработка программ с оператором условного перехода
Принцип работы оператора условного перехода в полной форме показан на примере разработки и выполнения программы с использованием графики.
Программа демонстрирует работу оператора условного перехода в полной форме. Блок-схема работы программы показана на рисунке 22. В случае, если пользователь вводит четное число – программа выводит на экран условное изображение девочки. При вводе нечетного числа программа рисует условное изображение мальчика.
Рисунок 22 – Блок-схема алгоритма программы usl1.bas
Код программы usl1.bas (основная программа)
DECLARE SUB GIRL ()
DECLARE SUB BOY ()
CLS
SCREEN 12
INPUT " N = "; N
IF N MOD 2 = 0 THEN
CALL GIRL
ELSE
CALL BOY
END IF
END
Результаты выполнения программы представлены на рисунках 23 - 24
Рисунок 23 – Результат выполнения программы usl1.bas при N=12
Код подпрограммы GIRL
SUB GIRL
CIRCLE (320, 180), 30, 15
LINE (320, 210)-(370, 300), 3
LINE (270, 300)-(320, 210), 3
LINE (270, 300)-(370, 300), 3