Файл: Основные структуры алгоритмов: сравнительный анализ и примеры их использования.pdf

Пример записи алгоритма на школьном языке АЯ:

алг Сумма квадратов (арг цел n, рез цел S)

дано | n > 0

надо | S = 1*1 + 2*2 + 3*3 + ... + n*n

нач цел i

ввод n; S:=0

нц для i от1 доn S:=S + i*i

кц

вывод "S = ", S

кон

Таким образом, различают алгоритмы нескольких видов в зависимости от цели, начальных условий задачи, путей ее решения и определения действий исполнителей. Выделяют механические алгоритмы, или детерминированные, жесткие (например, алгоритм работы машины, двигателя и т.п.); гибкие алгоритмы, например стохастические, т.е. вероятностные и эвристические.

Относительно понятия алгоритма различают три типа алгоритмических моделей.

А также различаю способы описания алгоритмов в зависимости от языка описания, который определяется тем, для какого исполнителя предназначен алгоритм. Это могут быть формы записи алгоритма: словесная – записывается на естественном языке; графическая – с помощью блок-схемы или в виде псевдокодов.

Глава 2. Структуры алгоритмов

2.1 Основные алгоритмические конструкции

В алгоритмическом языке реализуется преобразование величин по операторам (командам), которые располагаются в заданной последовательности. Логическая структура любого алгоритма представлена тремя типами алгоритмических конструкций:

- линейная или последовательная;

- разветвляющаяся;

- циклическая.

Особенность базовых структур состоит в том, что они имеют один вход и один выход.

Алгоритмы линейной структуры представлены последовательным выполнением действий одно за другим (рис. 1 [6, с. 9]).

Рисунок 1. Блок-схема линейного алгоритма

Прямоугольник, показанный на рисунке, может представлять как одну единственную команду, так и множество операторов, которые необходимы для выполнения сложной обработки данных.

Пример линейного алгоритма.

Даны длины трех сторон треугольников – a, b, c. Необходимо вычислить площадь – S, и периметр треугольника – P. Для нахождения площади можно воспользоваться формулой Герона: ???? = ????r(r − a)(r − b)(r − c), где r – полупериметр. Входные данные: a, b, c. Выходные данные: S, P.

Алгоритм представлен в виде блок-схемы на рис. 2 [6 с. 9 – 10].

---

Рисунок 2. Пример линейного алгоритма

Примечательно, что в указанных блоках знак «=» не означает математическое равенство, он означает операцию присваивания. Команды записываются с помощью операции присваивания. Присваивание переменной какого-либо значения или присваивание одной переменной значения другой переменной является наиболее часто выполняемым действием в программе, написанной на любом языке программирования.

Переменной, которая стоит слева от оператора, присваивается значение, указанное справа. Данное значение может быть или определено, или его нужно вычислить с помощью выражения. Как пример, операция r = (a+b+c)/2 – имеет смысл (переменной r присвоить значение (a+b+c)/2), а выражение (a+b+c)/2 = r – бессмыслица.

Разветвленная структура отличается тем, что в зависимости от выполнения или невыполнения какого-либо условия производятся различные последовательности действий. При этом последовательность таких действий называется ветвью алгоритма. На рис. 3 представлены алгоритмы полной и неполной разветвленной структуры [6, с. 10].

Рисунок 3. Полный и неполный разветвленный алгоритм

На практике редко предоставляется решить задачи в виде алгоритмов линейных структур. Чаще вычисления осуществляются то по одним, то по другим формулам, в зависимости от каких-либо промежуточных результатов. Получается, что при выполнении некоторых логических условий, вычислительный процесс осуществляется по одной или другой ветви.

Условием в разветвляющемся алгоритме может быть любое понятное исполнителю утверждение, которое может быть соблюдено (быть истинным) или не соблюдено (быть ложным). Такого рода утверждения описываются или словами или формулой.

Таким образом, различают два вида условий: простые и составные. Простое условие – это выражение, которое состоит из двух арифметических выражений или двух текстовых величин. При этом они связаны знаками: < (меньше), > (больше), >= (больше или равно), = (равно), о (не равно).

Составное условие строятся из двух или более простых выражений, которые связаны логическими операциями: И, ИЛИ, НЕ.

В качестве примера разветвленного алгоритма можно рассмотреть блок-схему алгоритма решения квадратного уравнения (Рис. 4 [1, c. 6]).

Рисунок 4. Блок-схема алгоритма решения квадратного уравнения

Можно рассмотреть и такой пример.

---

Необходимо упорядочить три числа: a, b, c по возрастанию таким образом, чтобы переменной a соответствовало самое маленькое число, b – среднее, c – самое большое.

Чтобы решить данную задачу, используют метод перестановок, благодаря которому последовательно сравниваются значения переменных а < b, затем а < c, потом b < c.

Если выполняется первое условие: а < b, то происходит переход к следующему условию: а < c. Если нет, то происходит перестановка значений соответствующих переменных, и после этого осуществляется переход к следующему условию.

В связи с тем, что в ПК каждая величина храниться в отдельной ячейке памяти, то нельзя сделать перестановку a = b; b = a. Иначе в обоих переменных a и b окажется значение b. Чтобы осуществить перестановку двух переменных a и b используют вспомогательную переменную h. И перестановка будет иметь следующий вид: h = a, a = b, b = h. (рис. 5) [5].

Рисунок 5. Пример разветвляющегося алгоритма с перестановкой двух переменных

Для алгоритма циклической структуры характерно выполнение повторяющейся последовательности действий, которая называется телом цикла, в зависимости от выполнения или невыполнения какого-либо условия. [7, с. 23]

Существует вложенный цикл, который находится внутри тела другого цикла. И итерационный цикл, число повторений которого не задается, а определяется в ходе выполнения цикла. Одно повторение называется итерацией. [11, с. 13]

Различают алгоритмы циклической структуры трех типов. На рис. 6 изображен цикл с предусловием, а на рис. 7 – цикл с постусловием [6, с. 11 – 12]. Данные циклы взаимосвязаны, но и имеют некоторые отличия:

- в цикле с предусловием - условия проверяются до тела цикла

в цикле с постусловием – после тела цикла;

- в цикле с предусловием – тело цикла может не выполняться ни разу

в цикле с постусловием - тело цикла выполняться хотя бы один раз;

- в цикле с предусловием – проверяются условия продолжения цикла

в цикле с постусловием – проверяются условия выхода из цикла.

Рисунок 6. Алгоритм циклической структуры с предусловием

Рисунок 7. Алгоритм циклической структуры с постусловием

И третий тип алгоритма циклической структуры – цикл с параметром. В таком цикле число повторений цикла однозначно определено и задается с помощью начального, конечного значений параметра и шагом его значения (рис. 8). [9, с. 17]

---

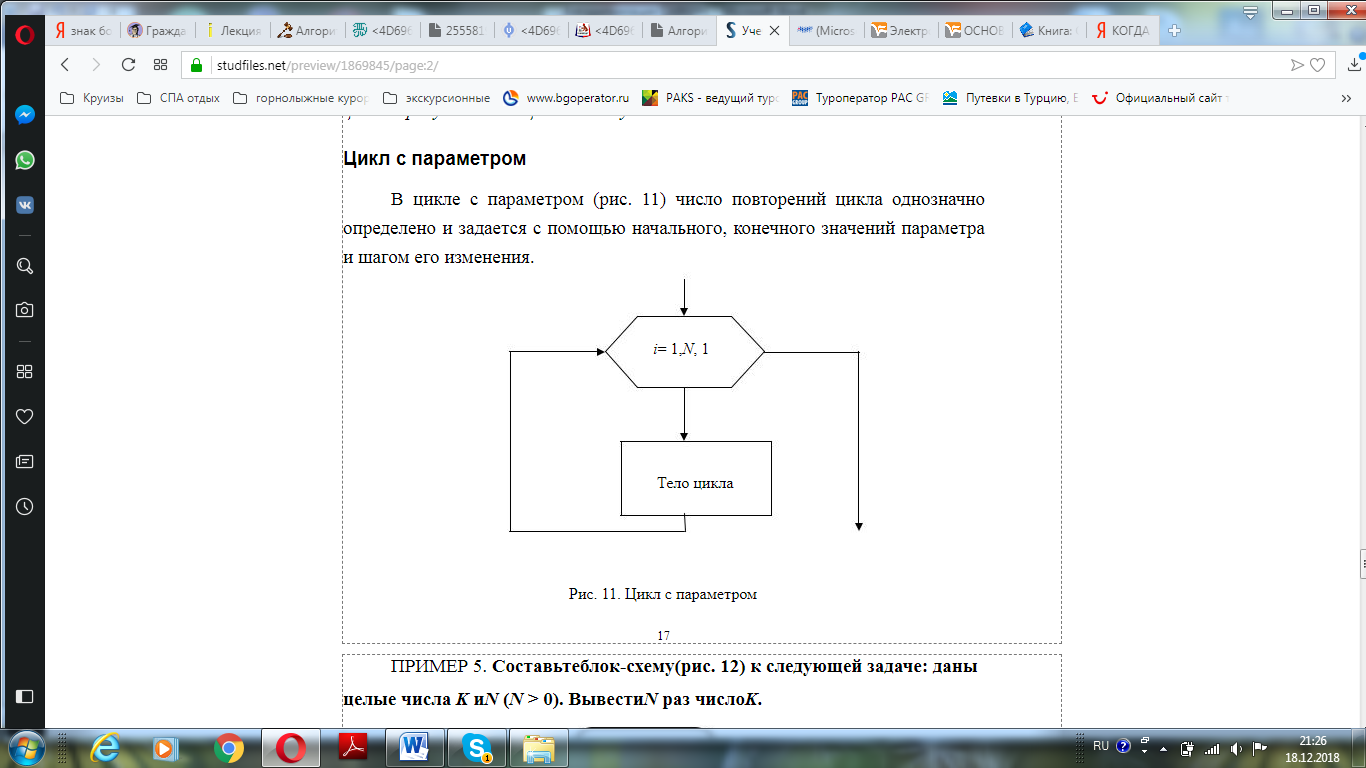
Рисунок 8. Цикл с параметром

Цикл с параметром выполняется следующим образом:

1. параметр цикла принимает начальное значение;

2. если параметр цикла не превышает конечного значения, выполняется тело цикла, иначе – выход из цикла, переход к следующей команде алгоритма.

3. параметр цикла изменяется на единицу или на заданный шаг;

4. переход к пункту 2.

При написании условных циклических алгоритмов следует помнить следующее. Во-первых, чтобы цикл имел шанс когда-нибудь закончиться, содержимое его тела должно обязательно влиять на условие цикла. Во-вторых, условие должно состоять из корректных выражений и значений, определенных еще до первого выполнения тела цикла.

Обязательные блоки для организации цикла:

1. Установка начального значения параметра цикла.
2. Изменять переменную перед каждым новым повторением цикла.
3. Проверка условия достижения конечного значения параметра

цикла.

1. Изменение параметра цикла, т.е. переходить к его началу, если он не закончен, или выходить из него по окончании.

Последние три функции выполняются многократно.

Переменные, которые изменяются в цикле, называются параметрами цикла. В одном цикле может быть несколько параметров. Основная сложность в этом процессе заключается в выявлении закономерности изменения параметров.

Для построения разветвляющихся и циклических структур алгоритма в алгоритмическом языке используются составные операторы такие, как операторы ветвления и цикла.

Оператор ветвления имеет вид: если условие то серия 1 иначе серия 2 все. В зависимости от итога проверки условия выполняется только одна из двух серий, входящих в команду ветвление. Если условие соблюдено, то следует выполнять серию 1, если то серию 2. Оператор ветвления используется и в сокращенной форме: если условие то серия все.

Если условие соблюдено, необходимо выполнить серию команд, следующую в записи алгоритма за служебным словом то, в противном случае, пропуская серию, перейти к выполнению команды, следующей за командой ветвления (после служебного слова все).

Для структуры ветвления существует четыре основных варианта записи:

если – то;

если – то – иначе;

выбор;

выбор – иначе.

Оператор выбора будет использоваться в случаях, если необходимо выбрать альтернативу их трех возможностей и более. [3, с. 31]

Таким образом, основные структуры алгоритмов представляют собой определенный набор блоков для выполнения типичных последовательностей действий. Основными алгоритмическими структурами являются: линейные, разветвляющиеся и циклические.

---

В линейных действия осуществляются последовательно одно за другим. В разветвляющихся действия выполняются по одной из возможных ветвей решения задачи. В циклической структуре некоторая часть операции выполняется многократно.

Особенности применения алгоритмических структур

Необходимость в создании алгоритмов обусловлена отказом от бессистемного оператора, преимуществом использования структурированных операторов, пошаговой детализации, т.е. создание структурного программирования.

Любая программа согласно структурному подходу строится с использованием трех основных типов блоков, указанных в предыдущем параграфе.

Выбор того или иного типа построения алгоритма зависит от условий решаемой задачи. Если блок предусматривает проверку логического условия, в зависимости от которого выполняется либо один, либо другой операторы, то в данном случае задача будет иметь вид структуры разветвленной. Если выполняется последовательность операторов один за другим без выбора условий, то это линейная структура алгоритма. Она имеет один вход и один выход. И если же необходимо многократно повторять выполнение какого-либо оператора, пока выполняется определенное логическое условие, то это блок цикла. Указанными параметрами характеризуются принципиальные отличия алгоритмических структур.

Однако при конструировании программ указанные типы блоков соединяются в одну цепочку блоков так, что выход одного блока подсоединяются ко входу следующего. В результате получается линейная структура.

Такая структура значительно облегчает чтение и понимание программы и упрощает доказательство ее правильности. Поэтому любая программа может рассматриваться как единый функциональный блок с одним входом и одним выходом. [13, с. 14]

Таким образом, при создании программ используются все типы структур алгоритмов.

При конструировании алгоритма и выборе того или иного типа, первоначально рассматривается вся задача целиком . Затем задача разбивается на более мелкие подзадачи и так далее, пока не будут получены такие подзадачи, которые легко кодируются на выбранном языке программирования. Такое программирование называется нисходящим. При таком процессе соблюдается строгая дисциплина программирования, т.е. разбиение на подзадачи осуществляется путем применения только рассмотренных типов конструкций. И в результате получается хорошо сконструированная программа.

Алгоритмы линейной структуры используются для решения простейших вычислений по формулам.

---