Добавлен: 15.11.2018
Просмотров: 797
Скачиваний: 16
Содержание:
-
Реферат……………………………………………………2
-
Разработка структурной схемы операционного устройства………………………………………………...3
-
Разработка микропрограммы выполнения заданной арифметической операции и структурно-операционной схемы операционного автомата………………………4
-
Разработка устройства управления выполнением операции (управляющего автомата) с жесткой логикой……………………………………………………11
-
Разработка устройства управления выполнением операции (управляющего автомата) с программируемой логикой……………………………………………………16
-
Иллюстрация функционирования операционного устройства на заданных числах………………...
1. Реферат
Курсовая работа содержит Чертежи на 3-х ватманах и пояснительную записку:
1-ый лист включает содержательную и отмеченную закодированную ГСА, функционально-логическую схему операционного автомата.
2-ой лист включает функционально-логическую схему управляющего автомата на жесткой логике.
3-ий лист включает закодированную и размеченную ГСА, функционально-логическую схему управляющего автомата на программируемой логике.
В данной пояснительной записке приведены расчеты и теоретические изыскания, необходимые для выполнения задачи поставленной в пункте 1.
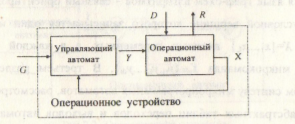
2. Разработка структурной схемы операционного устройства
Поскольку в любой системе цифровой обработки информации можно выделить операционный и управляющий блоки, то проектируемый автомат можно представить в следующем виде совокупности управляющего и операционного автоматов:
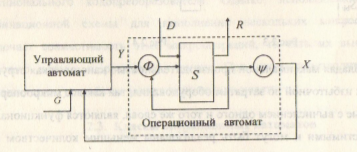
Функциональная и структурная организация операционного устройства базируется на принципах микропрограммного управления. Управляющий автомат в операционном устройстве формирует набор управляющих сигналов Y под воздействием осведомительных сигналов X, поступающих в автомат и реализующих микропрограмму работы дискретного устройства. При этом функция операционного автомата состоит в непосредственном выполнении заданного набора операций над словами множества D с целью вычисления множества выходных слов R.
Порядок выполнения операций в дискретном устройстве будет определяться микропрограммой, представляющей совокупность микроопераций и логических условий.
Рассмотрим синтез управляющего и операционного автоматов в связи с техническим заданием (см. п.1 пояснительной записки) подробнее в следующих пунктах пояснительной записки.
3. Разработка микропрограммы выполнения заданной арифметической операции и структурно-операционной схемы операционного автомата
Функция операционного автомата сводится к вводу, выводу и хранению слов информации, выполнению микроопераций и вычислению логических условий.
В состав операционного автомата входит (см. рис.4.1):
1) память S, предназначенная для фиксации входных и выходных значений, а также промежуточных результатов
2) функции преобразователи j, предназначенные для вычисления содержимого памяти автомата.
3) функциональные преобразователи Ф предназначенные для вычисления логических условий.
Поскольку разработка операционного автомата сильно зависит от критериев (требований к быстродействию и стоимости) обратимся к техническому заданию.
Критерием для разработки нашего автомата является максимальное быстродействие (см. п.1. пояснительной записки) поэтому при выполнении операции затраты оборудования в комбинационной части автомата нужно минимизировать.
Построим структуру операционного автомата производительность которого не ниже производительности автомата с канонической структурой, а затраты оборудования минимальны.
Операционный автомат, структура которого обеспечивает одновременное выполнение всех функций несовместимых микроопераций при использовании возможного минимального количества комбинационных схем выделяется в класс I-автоматов.
Синтез таких автоматов сводится к преобразованию совокупности микроопераций в множество обобщенных операторов, которые используются для построения структурной схемы I-автоматов.
Этапы синтеза:
-
Множество операций Y (y1, y2, …, ym) разбивается на подмножеств F Y1, Y2, …, YM.
-
На подмножестве Yi выделяют несколько классов эквивалентных микроопераций.
-
Для каждого класса Kij содержащего не менее 2-х эквивалентных микроопераций строятся обобщенные операторы.
-
На основе содержательного графа с использованием обобщенных операторов строится структура I-автомата.
Нам необходимо реализовать операцию умножения. Воспользуемся третьим алгоритмом умножения, выбранным с учетом критерия (См п.1), так как он менее затратен, чем другие, в связи с тем, что сдвиг и передача информации не совмещены во времени.
Алгоритм умножения старшими разрядами множителя со сдвигом множимого вправо. Знак результата определяется сложением по модулю два знаков множителей
1. Происходит подготовка регистров.
2. Находится значение порядка результата.
3. Происходит сдвиг множимого вправо на 1 разряд.
4. Анализируется старший разряд множителя. Если он равен 1, то происходит сложение частичных сумм и множимого, если он равен 0, то переходим к пункту 5.
5. Происходит сдвиг множителя влево на 1 разряд.
6. Затем переходим к пункту 3. И так до тех пор пока не закончим умножение (число повторов определяется числом разрядов мантиссы множителя)
Для более точного описания алгоритма необходимо составить программу на ф-языке и представить ее в виде содержательной граф-схемы алгоритма.
Предварительно же необходимо рассчитать разрядную сетку. Расчет будем производить исходя из погрешности и диапазона представления чисел. (см. п.1 пояснительной записки.)
Расчет разрядной сетки:
Из диапазона представления чисел найдем число бит необходимых под порядок, а из погрешности число бит необходимых для мантиссы.
![]()
![]()
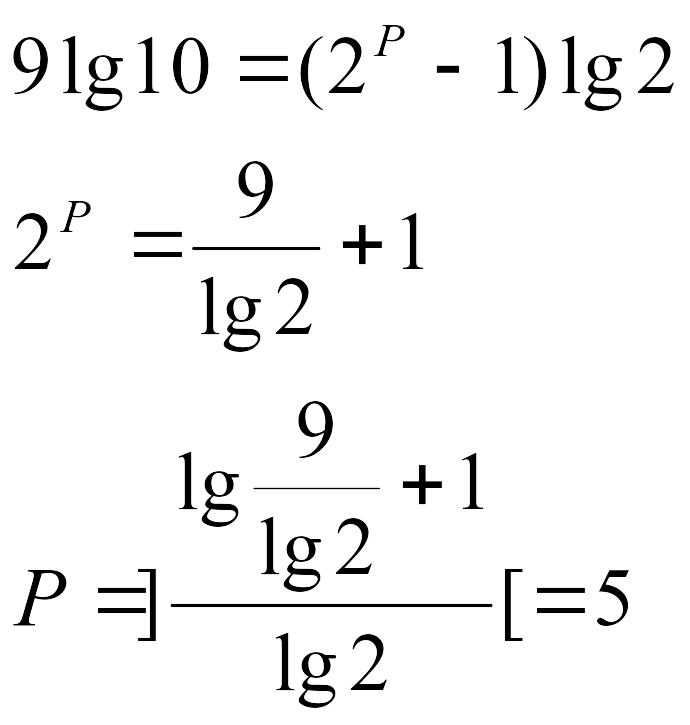
![]()
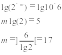
Так как по шине данные передаются по 1 байту поэтому доведем разрядную сетку до кратной 8.
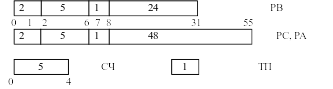
РА – множимое
РВ – множитель
РС – произведение
СЧ – счетчик
ТП – триггер переполнения
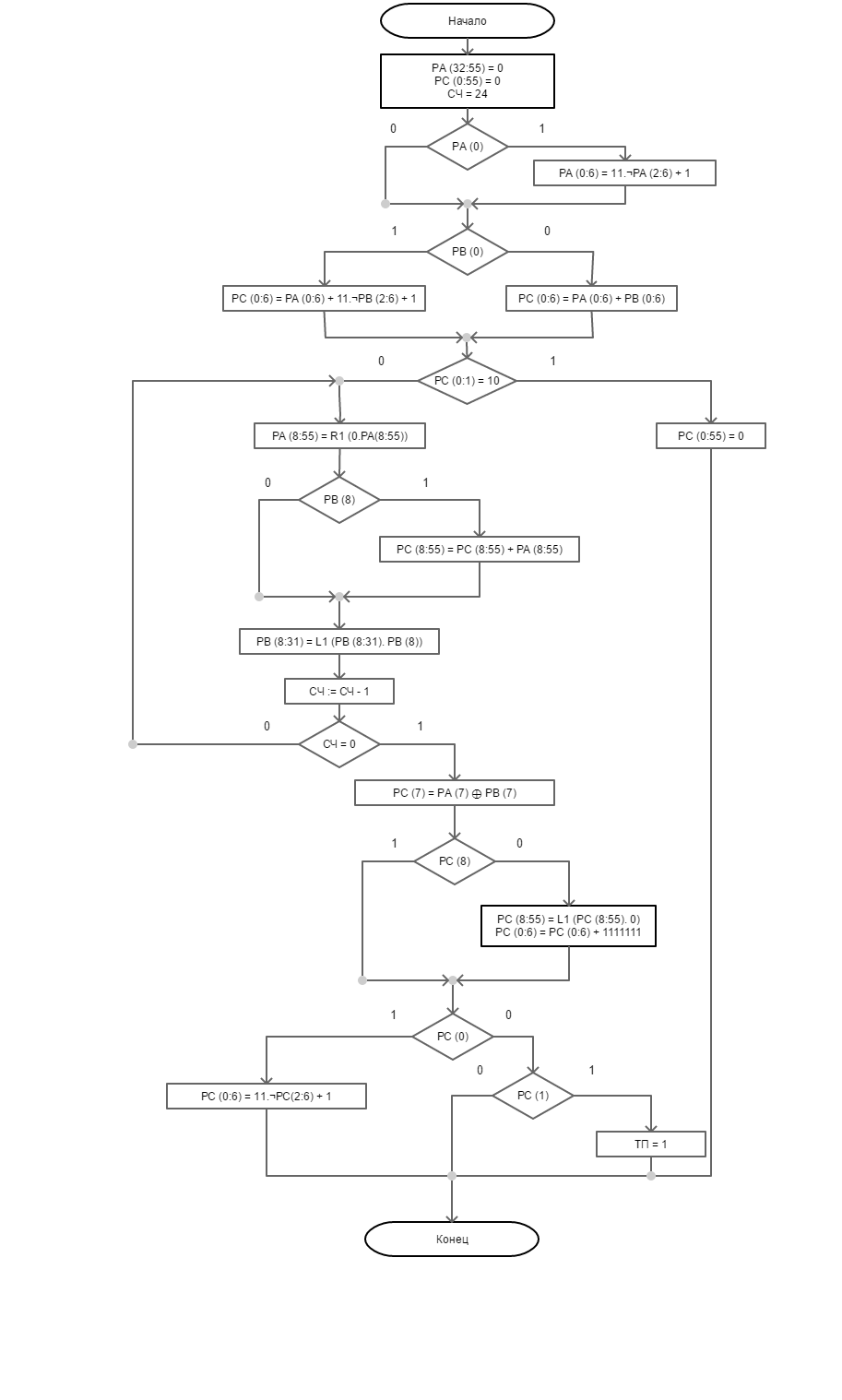
Теперь закодируем нашу ГСА (См. лист 1 чертежа):
Обозначим все операции через yi;
Обозначим все условия через xi;
Теперь составим таблицу микроопераций и управляющих сигналов им соответствующих.
|
Y |
Микрооперации |
x |
Управляющие сигналы |
|
|
y1 |
РА (32:55) = 0 |
x1 |
РА (0) |
|
|
y2 |
РС (0:55) = 0 |
x2 |
РВ (0) |
|
|
y3 |
СЧ = 2410 |
x3 |
РС (0:1) = 10 |
|
|
y4 |
РА (0:6) = 11. ¬РА (2:6) + 1 |
x4 |
РВ (8) |
|
|
y5 |
РС = РА (0:6) + 11. ¬РВ (2:6) + 1 |
x5 |
СЧ = 0 |
|
|
y6 |
РС (0:6) = РА (0:6) + РВ (0:6) |
x6 |
РС (8) |
|
|
y7 |
РА (8:55) = R1(0. РА (8:55)) |
x7 |
РС (0) |
|
|
y8 |
РС (8:55) = РС (8:55) + РА (8:55) |
x8 |
РС (1) |
|
|
y9 |
РВ (8:31) = L1 (РВ (8:31). РВ(8)) |
|
||
|
y10 |
СЧ := СЧ – 1 |
|
||
|
y11 |
РС (7) = РА (7) ⊕ РВ (7) |
|
||
|
y12 |
РС (8:55) = L1 (РС (8:55). 0) |
|
||
|
y13 |
РС (0:6) = РС (0:6) + 1111111 |
|
||
|
y14 |
ТП = 1 |
|
||
|
Y15 |
РС(0:6) = 11. ¬РС(2:6) + 1 |
|
||
Синтез I-автомата
1) По таблице микроопераций (м/о) выделяем множества внутренних слов, которым соответствуют м/о:
2) На подмножестве Yi выделяем классы эквивалентных м/о kij:
|
Y |
К |
классы |
операция |
|
YРА |
КРА(1) |
y1 |
Обнуление |
|
КРА(2) |
y4 |
Сложение |
|
|
КРА(3) |
y7 |
Сдвиг вправо |
|
|
YРВ |
КРВ |
y9 |
Сдвиг влево |
|
YРС |
КРС(1) |
y2 |
Обнуление |
|
КРС(2) |
y5, y6, y8,y13, y15 |
Сложение |
|
|
КРС(3) |
y11 |
Сложение по модулю 2 |
|
|
КРС(4) |
y12 |
Сдвиг влево |
|
|
YСЧ |
КСЧ(1) |
y3 |
Присваивание |
|
КСЧ(1) |
y10 |
Вычитание |
|
|
YТП |
КТП |
y14 |
Присваивание |
3) Для kij, содержащего не менее двух эквивалентных м/о, строится обобщённый оператор.
4) На основе содержательной ГСА с использованием обобщённых операторов строится структура I-автомата.
Зная классы эквивалентных микроопераций, можно построить для каждого класса обобщенный оператор, а затем легко синтезировать схему.
В схеме мы будем использовать следующие структурные элементы:
Шина:
Шина это совокупность цепей для передачи информации.
Различают информационную шину и управляющую шину.
И нформационная
шина:
нформационная
шина:
Управляющая шина:
В управляющей шине сигнал S не пройдет, если yi.
Регистр:
Регистр – совокупность триггеров.
О бозначается:
бозначается:
Значения можно присваивать, как отдельным группам разрядов, так и всему регистру в целом. Считывать можно и из всего регистра сразу, и из отдельных его разрядов.
О бозначается:
бозначается:
Регистр S, с n+1 разрядами.
Счетчик:
С овокупность
триггеров. Реализует счет.
овокупность
триггеров. Реализует счет.
Обозначается:

Преобразователь:
Функция-преобразователь, это функция определяемая разработчиком. Обозначается:

Примером может служить преобразователь числа в дополнительный код:
Сумматор:
Служит для выполнения операции сложения двух чисел в двоичном коде.
Обозначается:
Двухвходовой сумматор Трехвходовой сумматор
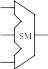

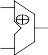
Отдельный вид сумматора – «сумматор по модулю два». Он реализует операцию сложения «по модулю два». Обозначается:
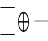
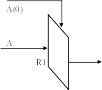
Сдвигатель:
Реализует операцию сдвига влево или вправо. Обозначается: R1 – сдвигает в право на 1 бит, L1 – влево на один бит.
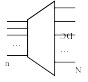
Комбинационная схема сдвигателя выглядит следующим образом:
Дешифратор:
Преобразует n-разрядный двоичный код в унитарный код.
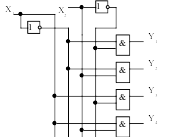
Компаратор:
Эта схема производит сравнение. Обозначается:

Например, проверка счетчика на равенство нулю:

Мультиплексор:
Мультиплексор – это схема обеспечивающая подключение 1-ой из входных шин на выход:

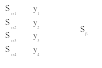
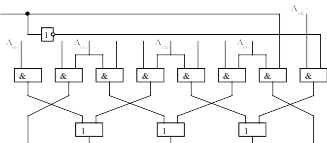
4. Разработка устройства управления выполнением операции (управляющего автомата) с жесткой логикой
Управляющий автомат с жесткой логикой может быть построен на основе автоматов Мили или Мура.
Автомат мили в нашей ГСА имеет 10 состояний а мура 14 состояний. И тот и другой случай соответствует 4 триггерам, поэтому выбираем автомат мура, т.к. он быстрее.
Проведём анализ содержательной ГСА на предмет совместимости м/о, следующих друг за другом.
Необходимо произвести отметку закодированной ГСА.
Входы различных вершин, за исключением конечной, должны быть отмечены разными символами.
Для автомата Мура отметка производиться следующим образом:
-
Символом а1 отмечаются начальная и конечная вершины;
-
Все остальные операторные вершины, кроме уже отмеченных а1, отмечаются как а2…аm, но не более чем одним символом.
В качестве метода борьбы с гонками выберем в нашем автомате противогоночное кодирование, а в качестве элементов памяти синхронные RS - триггеры, из-за указанного в техническом задании критерия.
Тогда структурная схема нашего автомата будет следующей:
Построим закодированную отмеченную ГСА. См. лист 1 чертежа.
Построим по отмеченному графу структурную таблицу автомата:
|
K(am) |
Аm (yn) |
K(as) |
As |
X(as, am) |
F(as, am) |
|||||||
|
S1 |
S2 |
S3 |
S4 |
R1 |
R2 |
R3 |
R4 |
|||||
|
0000 |
a1 |
0010 |
a6 |
1 |
|
|
|
|
|
|
1 |
|
|
1100 |
a11 |
|
|
|
|
|
1 |
1 |
|
|
||
|
1101 |
a12 |
|
|
|
|
|
1 |
1 |
|
1 |
||
|
0011 |
a13 |
1 |
|
|
|
|
|
|
1 |
1 |
||
|
0100 |
a14 |
1 |
|
|
|
|
|
1 |
|
|
||
|
0001 |
a2 y1, y2, y3 |
0000 |
a1 |
1 |
|
|
|
1 |
|
|
|
|
|
0101 |
a3 y4 |
0001 |
a2 |
x1 |
|
1 |
|
|
|
|
|
|
|
0110 |
a4 y5 |
0001 |
a2 |
|
|
1 |
1 |
|
|
|
|
1 |
|
0101 |
a3 |
x2 |
|
|
1 |
|
|
|
|
1 |
||
|
0111 |
a5 y6 |
0001 |
a2 |
|
|
1 |
1 |
|
|
|
|
|
|
0101 |
a3 |
|
|
|
1 |
|
|
|
|
|
||
|
0010 |
a6 y2 |
0110 |
a4 |
x3 |
|
|
|
|
|
1 |
|
|
|
0111 |
a5 |
x3 |
|
|
|
|
|
1 |
|
1 |
||
|
1011 |
a7 y7 |
0110 |
a4 |
|
1 |
|
|
1 |
|
1 |
|
|
|
0111 |
a5 |
|
1 |
|
|
|
|
1 |
|
|
||
|
1010 |
a10 |
|
|
|
|
1 |
|
|
|
|
||
|
1000 |
a8 y8 |
1011 |
a7 |
x4 |
|
|
|
|
|
|
1 |
1 |
|
1001 |
a9 y9 |
1000 |
a8 |
1 |
|
|
|
1 |
|
|
|
|
|
1011 |
a7 |
|
|
|
|
|
|
|
1 |
|
||
|
1010 |
a10 y10 |
1001 |
a9 |
1 |
|
|
1 |
|
|
|
|
1 |
|
1100 |
a11 y11 |
1010 |
a10 |
x5 |
|
1 |
|
|
|
|
1 |
|
|
1101 |
a12 y12,y13 |
1100 |
a11 |
|
|
|
|
1 |
|
|
|
|
|
0011 |
a13 y4 |
1100 |
a11 |
x6x7 |
|
|
1 |
1 |
1 |
1 |
|
|
|
1101 |
a12 |
x7 |
|
|
1 |
|
1 |
1 |
|
|
||
|
0100 |
a14 y14 |
1100 |
a11 |
|
|
|
|
|
1 |
|
|
|
|
1101 |
a12 |
|
|
|
|
|
1 |
|
|
1 |
||
При кодировании состояний исходят из того, что сложность схем формирования функции возбуждения находится в пропорциональной зависимости от количества единиц в коде состояний.
Из-за того что в ГСА существует цикл из нечетного кол-ва переходов (3-х) то использовать соседнее кодирование запрещено. Тогда закодируем методом развязывания пар.
Тогда:
Автомат, в котором все пары переходов осуществляемые под воздействием одного и того же сигнала являются развязанными, то в гонки в таком автомате отсутствуют. Развязыванию подлежат пары у которых пересечение индексов равно нулю.
|
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
||
|
a1-a6 |
|
a1-a13 |
|
a1-a14 |
|
a2-a1 |
a9-a8 |
|
|
||
|
|
|
|
|
|
a9-a8 |
|
a10-a9 |
|
|
||
|
|
|
|
a9-a8 |
|
a10-a9 |
|
|
|
|
||
|
|
a9-a8 |
|
a10-a9 |
|
|
|
|
|
|
||
|
|
a10-a9 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||||||
|
a1 |
0 |
0 |
0 |
0 |
|
||||||
|
a2 |
0 |
0 |
0 |
1 |
|
||||||
|
a3 |
0 |
1 |
0 |
1 |
|
||||||
|
a4 |
0 |
1 |
1 |
0 |
|
||||||
|
a5 |
0 |
1 |
1 |
1 |
|
||||||
|
a6 |
0 |
0 |
1 |
0 |
|
||||||
|
a7 |
1 |
0 |
1 |
1 |
|
||||||
|
a8 |
1 |
0 |
0 |
0 |
|
||||||
|
a9 |
1 |
0 |
0 |
1 |
|
||||||
|
a10 |
1 |
0 |
1 |
0 |
|
||||||
|
a11 |
1 |
1 |
0 |
0 |
|
||||||
|
a12 |
1 |
1 |
0 |
1 |
|
||||||
|
a13 |
0 |
0 |
1 |
1 |
|
||||||
|
a14 |
0 |
1 |
0 |
0 |
|
||||||
![]()
![]()
|
|
α |
β |
|
|
|
|
|
a1 |
00 |
00 |
|
a2 |
00 |
01 |
|
a3 |
01 |
01 |
|
a4 |
01 |
10 |
|
a5 |
01 |
11 |
|
a6 |
00 |
10 |
|
a7 |
10 |
11 |
|
a8 |
10 |
00 |
|
a9 |
10 |
01 |
|
a10 |
10 |
10 |
|
a11 |
11 |
00 |
|
a12 |
11 |
01 |
|
a13 |
00 |
11 |
|
a14 |
01 |
00 |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
α = {1, 3, 4, 5} β = {2, 6, 7, 8}
(1) = 00 (4) = 10 (2) = 00 (7) = 10
(3) = 01 (5) = 11 (6) = 01 (8) = 11
Составим по таблице аналитические выражения функций сигналов возбуждения и выходов в базисе 2-И-НЕ.
При преобразовании функций будем использовать следующие правила алгебры логики:
1) ab
=
![]()
2)
![]()
3)
![]()
4)
![]()
1) функции возбуждения:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
2) выходные сигналы:
y1 = a2
y2 = a2 v a6
y3=![]()
y4=![]()
y5=![]()
y6=![]()
y7=![]()
y8=![]()
y9=![]()
y10=![]()
y11=![]()
y12 = a12
y13 = a12
y14 = a14
y15 = a13
5. Разработка устройства управления выполнением операции (управляющего автомата) с программируемой логикой
Принцип микропрограммного управления был предложен Wilkes в 1951 г.
И впервые был реализован IBM 8/360.
Последовательность управляющих сигналов в таком устройстве задаётся микропрограммой хранимой в постоянном запоминающем устройстве (ПЗУ).
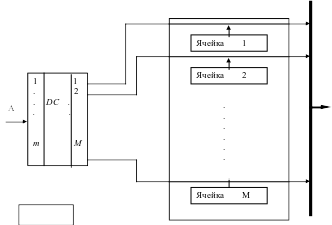
накопитель
УУ с программируемой логикой содержит:
-
Регистр адреса микрокоманд.
-
Регистр микрокоманд.
-
Схему формирования адреса следующей микрокоманды.
При горизонтальном кодировании под каждый управляющий сигнал выделяется один разряд, что позволяет в рамках одной микрокоманды формировать любые сочетания микроопераций, но приводит к большим затратам на хранение и низкой эффективности использования памяти.
При вертикальном кодировании достигается минимальная длина операционной части микрокоманды, равная ]log2 Мо[, где Мо – количество микрокоманд. При этом в каждой микрокоманде кодируется только одна операция. Так как наш операционный автомат относится к классу I-автоматов, позволяющим достигнуть максимальную производительность с использованием одновременно нескольких управляющих сигналов, вертикальное кодирование не подходит.
При смешанном кодировании, горизонтально-вертикальном, вся совокупность м/о группируется на несовместимые м/о и каждая группа кодируется вертикально и дешифруется отдельно.
Отметим закодированную ГСА методом смешанного кодирования для принудительной адресации. Тогда количество бит, используемых под ПЗУ = 18 бит/ команда * 18 м/к =324 бит.
Узнаем формат ячейки ПЗУ
Для начала необходимо разбить м/о по полям операционной части м/к так, что внутри каждого поля они были несовместимы между собой. Построим матрицу совместимости. М/о выполняющиеся одновременно кодируются 1. Например y1,y2,y3.
Матрица совместимости
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
|||||||||||||||||||
|
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
s1 |
|||||||||||||||||||
|
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
s2 |
|||||||||||||||||||
|
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
s3 |
|||||||||||||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
s4 |
|||||||||||||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
s5 |
|||||||||||||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
s6 |
|||||||||||||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
s7 |
|||||||||||||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
s8 |
|||||||||||||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
s9 |
|||||||||||||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
s10 |
|||||||||||||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
s11 |
|||||||||||||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
s12 |
|||||||||||||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
s13 |
|||||||||||||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
s14 |
|||||||||||||||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
s15 |
|||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
||||||||||||||||
|
|
|
R1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
||||||||||||||||
|
|
S1 ∩ R1 = ∅ |
R1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
||||||||||||||||
|
|
S2 ∩ R1 ≠ ∅ |
R2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
||||||||||||||||
|
|
R2 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|||||||||||||||||
|
|
S3 ∩ R1 ≠ ∅ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
S3 ∩ R2 ≠ ∅ |
R3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
||||||||||||||||
|
|
R3 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|||||||||||||||||
|
|
S4 ∩ R1 = ∅ |
R1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
||||||||||||||||
|
|
S5 ∩ R1 = ∅ |
R1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
||||||||||||||||
|
|
S6 ∩ R1 = ∅ |
R1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
||||||||||||||||
|
|
S7 ∩ R1 = ∅ |
R1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
||||||||||||||||
|
|
S8 ∩ R1 = ∅ |
R1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
||||||||||||||||
|
|
S9 ∩ R1 = ∅ |
R1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
||||||||||||||||
|
|
S10 ∩ R1 = ∅ |
R1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
||||||||||||||||
|
|
S11 ∩ R1 = ∅ |
R1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
|
||||||||||||||||
|
|
S12 ∩ R1 = ∅ |
R1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
|
||||||||||||||||
|
|
S13 ∩ R1 ≠ ∅ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
S13 ∩ R2 = ∅ |
R2 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
||||||||||||||||
|
|
S14 ∩ R1 = ∅ |
R1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
|
||||||||||||||||
|
|
S15 ∩ R1 = ∅ |
R1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
R1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
|
||||||||||||||||
|
|
|
R2 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
||||||||||||||||
|
|
|
R3 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
||||||||||||||||
Y1 = {y1,y4,y5,y6,y7,y8,y9,y10,y11,y12,y14,y15}
Y2 = {y2,y13}
Y3 = {y3}
Для удобства кодирования поместим по 5. несовместимых м/о в разные подмножества. Каждую м/о закодируем вертикальным кодированием в разных подмножествах.
|
X |
|
|
0001 |
1 |
|
0010 |
2 |
|
0011 |
3 |
|
0100 |
4 |
|
0101 |
5 |
|
0110 |
6 |
|
0111 |
7 |
|
1000 |
8 |
|
Код |
Y1 |
Y2 |
Y3 |
|
001 |
y1 |
y2 |
y3 |
|
010 |
y4 |
y5 |
y6 |
|
011 |
y7 |
y8 |
y9 |
|
100 |
y10 |
y11 |
y14 |
|
101 |
y12 |
y13 |
y15 |
Условия закодируем вертикально.
При естественной адресации микрокоманды в ПЗУ делят на управляющие и операционные микрокоманды. Управляющая микрокоманда:
|
1 |
X |
А |
При единичном условии X осуществляется по адресу из поля A, иначе выполняется следующая микрокоманда из ПЗУ
Операционная команда:
|
0 |
Y |
Y – поле операционной части, затем всегда выполняется следующая микрокоманда из ПЗУ.
Для моего алгоритма программа с естественной адресацией будет выглядеть так:
|
|
|
Х |
А1 |
|
Адрес |
К |
Y |
|
|
1 |
0 |
y1,y2,y3 |
|
|
2 |
1 |
1 |
12 |
|
3 |
1 |
2 |
14 |
|
4 |
0 |
y6 |
|
|
5 |
1 |
3 |
16 |
|
6 |
0 |
y7 |
|
|
7 |
1 |
4 |
28 |
|
8 |
0 |
y9 |
|
|
9 |
0 |
y10 |
|
|
10 |
1 |
5 |
18 |
|
11 |
1 |
0 |
6 |
|
12 |
0 |
y4 |
|
|
13 |
1 |
0 |
3 |
|
14 |
0 |
y5 |
|
|
15 |
1 |
0 |
5 |
|
16 |
0 |
y2 |
|
|
17 |
1 |
0 |
23 |
|
18 |
0 |
y11 |
|
|
19 |
1 |
6 |
21 |
|
20 |
0 |
y12,y13 |
|
|
21 |
1 |
7 |
24 |
|
22 |
1 |
8 |
26 |
|
23 |
0 |
0 |
0 |
|
24 |
0 |
y15 |
|
|
25 |
1 |
0 |
23 |
|
26 |
0 |
y14 |
|
|
27 |
1 |
0 |
23 |
|
28 |
0 |
y8 |
|
|
29 |
1 |
0 |
8 |
По условию задания – максимальная производительность, т.е. с минимальной длиной программы, выбираем из рассмотренных вариантов автомат с принудительной адресацией.
Можно было использовать 2 адресных поля, тогда бы мы избавились он одного безусловного перехода. Но такие изменения незначительны, а аппаратные затраты существенно больше, поэтому я использую одно адресное поле.
В принудительной адресации адрес следующей команды явно записан в микрокоманде. При смешанном кодировании формат ячейки выглядит так:
|
Y1 |
Y2 |
Y3 |
X |
A |
|||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
Закодируем ПЗУ:
|
|
Y1 |
Y2 |
Y3 |
X |
A |
|||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
|
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
|
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
|
3 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
|
4 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
|
5 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
|
6 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
7 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|
8 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
|
9 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
10 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
|
11 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
|
12 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
|
13 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
|
14 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
|
15 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|
16 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|
17 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
18 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
А = 13.75
В = 13
Переводим в двоичную С.С.
А = 1101.11 => 0.110111 * 24
В = 1101 => 0.1101 * 24
|
|
Знак Порядка |
порядок |
Знак мантиссы |
мантисса |
|
А |
00 |
00100 |
0 |
110111 (15:55) = 0 |
|
В |
00 |
00100 |
0 |
1101 (13:31) = 0 |
|
С |
00 |
00000 |
0 |
(8:55) = 0 |
1)А(0) = 0
2)B(0) = 0 => C (0:6) = B(0:6) + A(0:6) = 010002 (810)
3)С(0:1) = 10? (нет) =>
C= |00|01000|0|00000000000000…0
A > |00|00100|0|01101110000000…0 +
B(8)=1 ____________________________
C=C+A |00|01000|0|01101110000000…0
B < |00|00100|0|1010000…01
CЧ=24-1=23
C= |00|01000|0|01101110000000…0
A > |00|00100|0|00110111000000…0 +
B(8)=1 ____________________________
C=C+A |00|01000|0|10100101000000…0
B < |00|00100|0|010000…011
CЧ=23-1=22
C= |00|01000|0|10100101000000…0
A > |00|00100|0|00011011100000…0
B(8)=0
B < |00|00100|0|10000…0110
CЧ=22-1=21
C= |00|01000|0|10100101000000…0
A > |00|00100|0|00001101110000…0 +
B(8) = 1 ____________________________
C=C+A |00|01000|0|10110010110000…0
(дальше в В остались только 0 до конца счетчика, поэтому 21 такт счетчика автомат будет только сдвигать вправо регистр А и влево В ничего не складывая)
4)
![]() = 0
= 0
5) С(8) = 1 => C(0) = 0 => C(1) = 0 => C(0:55) ответ
13.75 * 13 = 178.75 = 10110010.11|
С= 0.1011001011 * 28 = 10110010.11
Ответы совпадают, значит устройство функционирует верно
Список использованной литературы.
-
Е.И. Зайцев Прикладная теория цифровых автоматов: Учебное пособие –М.: МГУПИ, 2008. – 74с.
-
Конспект лекций по Теории автоматов.
-
Марченков С.С. “Конечные автоматы” – М.:ФИЗМАТЛИТ, 2008. – 56 с.
-
В.А. Горбатов “Теория автоматов: учеб. для студентов втузов” – 2008.
-
Карпов Ю.Г. Теория автоматов. –СПб.: Издательский дом “Питер”, 2003. –208с.