Файл: Контрольная работа Заочники.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Методичка

Дисциплина: Информатика

Добавлен: 15.11.2018

Просмотров: 1435

Скачиваний: 6

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

ОБЩИЕ УКАЗАНИЯ

1. УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ

ВАРИАНТ КОНТРОЛЬНОЙ РАБОТЫ ВЫБИРАЕТСЯ СЛЕДУЮЩИМ ОБРАЗОМ

Берутся две последних цифры зачетки

2 Методические указания по решению практической задачи

Задание 1

Задание 2

Задание 3

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

ВАРИАНТЫ ЗАДАНИЙ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ

Вариант 1

Задание 1

Построить в разных системах координат графики функций:

при заданных значениях аргумента . Выполнить условное форматирование таблицы значений аргумента и функций, так чтобы ячейки значений в диапазонах: ;имели заливку разными цветами. Для функции определить наилучшее линейное приближение двумя способами: используя функцию ЛИНЕЙН и с помощью пункта меню Сервис | Анализ данных | Регрессия.


Задание 2


Построить в одной системе координат графики функций при . Вычислить определенный интеграл методом трапеций от функции


Задание 3


Построить поверхность при заданных значениях аргументов ; .


Вариант 2

Задание 1

Построить в разных системах координат графики функций:

при заданных значениях аргумента . Выполнить условное форматирование таблицы значений аргумента и функций, так чтобы ячейки значений в диапазонах: ;имели заливку разными цветами. Для функции определить наилучшее линейное приближение двумя способами: используя функцию ЛИНЕЙН и с помощью пункта меню Сервис | Анализ данных | Регрессия.


а)

б)

в)

Задание 2


Построить в одной системе координат графики функций при . Вычислить определенный интеграл методом трапеций от функции


Задание 3


Построить поверхность при заданных значениях аргументов ; .


Вариант 3

Задание 1

Построить в разных системах координат графики функций:

при заданных значениях аргумента . Выполнить условное форматирование таблицы значений аргумента и функций, так чтобы ячейки значений в диапазонах: ;имели заливку разными цветами. Для функции определить наилучшее линейное приближение двумя способами: используя функцию ЛИНЕЙН и с помощью пункта меню Сервис | Анализ данных | Регрессия.


а).

б)

в )

Задание 2


Построить в одной системе координат графики функций при . Вычислить определенный интеграл методом трапеций от функции


Задание 3

Построить поверхность при заданных значениях аргументов ; .



Вариант 4

Задание 1

Построить в разных системах координат графики функций:

при заданных значениях аргумента . Выполнить условное форматирование таблицы значений аргумента и функций, так чтобы ячейки значений в диапазонах: ;имели заливку разными цветами. Для функции определить наилучшее линейное приближение двумя способами: используя функцию ЛИНЕЙН и с помощью пункта меню Сервис | Анализ данных | Регрессия.


а).

б)

в)

Задание 2


Построить в одной системе координат графики функций при . Вычислить определенный интеграл методом трапеций от функции

Задание 3


Построить поверхность при заданных значениях аргументов ; .


Вариант 5

Задание 1

Построить в разных системах координат графики функций:

при заданных значениях аргумента . Выполнить условное форматирование таблицы значений аргумента и функций, так чтобы ячейки значений в диапазонах: ;имели заливку разными цветами. Для функции определить наилучшее линейное приближение двумя способами: используя функцию ЛИНЕЙН и с помощью пункта меню Сервис | Анализ данных | Регрессия.


а).

б)

в)

Задание 2


Построить в одной системе координат графики функций при . Вычислить определенный интеграл методом трапеций от функции


Задание 3


Построить поверхность при заданных значениях аргументов ; .


Вариант 6

Задание 1

Построить в разных системах координат графики функций:

при заданных значениях аргумента . Выполнить условное форматирование таблицы значений аргумента и функций, так чтобы ячейки значений в диапазонах: ;имели заливку разными цветами. Для функции определить наилучшее линейное приближение двумя способами: используя функцию ЛИНЕЙН и с помощью пункта меню Сервис | Анализ данных | Регрессия.


Задание 2


Построить в одной системе координат графики функций при . Вычислить определенный интеграл методом трапеций от функции


Задание 3


Построить поверхность при заданных значениях аргументов ; .



Вариант 7

Задание 1

Построить в разных системах координат графики функций:

при заданных значениях аргумента . Выполнить условное форматирование таблицы значений аргумента и функций, так чтобы ячейки значений в диапазонах: ;имели заливку разными цветами. Для функции определить наилучшее линейное приближение двумя способами: используя функцию ЛИНЕЙН и с помощью пункта меню Сервис | Анализ данных | Регрессия.


Задание 2


Построить в одной системе координат графики функций при . Вычислить определенный интеграл методом трапеций от функции


Задание 3


Построить поверхность при заданных значениях аргументов ; .



Вариант 8

Задание 1

Построить в разных системах координат графики функций:

при заданных значениях аргумента . Выполнить условное форматирование таблицы значений аргумента и функций, так чтобы ячейки значений в диапазонах: ;имели заливку разными цветами. Для функции определить наилучшее линейное приближение двумя способами: используя функцию ЛИНЕЙН и с помощью пункта меню Сервис | Анализ данных | Регрессия.


Задание 2


Построить в одной системе координат графики функций при . Вычислить определенный интеграл методом трапеций от функции


Задание 3


Построить поверхность при заданных значениях аргументов ; .



Вариант 9

Задание 1

Построить в разных системах координат графики функций:

при заданных значениях аргумента . Выполнить условное форматирование таблицы значений аргумента и функций, так чтобы ячейки значений в диапазонах: ;имели заливку разными цветами. Для функции определить наилучшее линейное приближение двумя способами: используя функцию ЛИНЕЙН и с помощью пункта меню Сервис | Анализ данных | Регрессия.


Задание 2


Построить в одной системе координат графики функций при . Вычислить определенный интеграл методом трапеций от функции


Задание 3


Построить поверхность при заданных значениях аргументов ; .



Вариант 10

Задание 1

Построить в разных системах координат графики функций:

при заданных значениях аргумента . Выполнить условное форматирование таблицы значений аргумента и функций, так чтобы ячейки значений в диапазонах: ;имели заливку разными цветами. Для функции определить наилучшее линейное приближение двумя способами: используя функцию ЛИНЕЙН и с помощью пункта меню Сервис | Анализ данных | Регрессия.



Задание 2


Построить в одной системе координат графики функций при . Вычислить определенный интеграл методом трапеций от функции


Задание 3


Построить поверхность при заданных значениях аргументов ; .



Вариант 11

Задание 1

Построить в разных системах координат графики функций:

при заданных значениях аргумента . Выполнить условное форматирование таблицы значений аргумента и функций, так чтобы ячейки значений в диапазонах: ;имели заливку разными цветами. Для функции определить наилучшее линейное приближение двумя способами: используя функцию ЛИНЕЙН и с помощью пункта меню Сервис | Анализ данных | Регрессия.


Задание 2


Построить в одной системе координат графики функций при . Вычислить определенный интеграл методом трапеций от функции


Задание 3


Построить поверхность при заданных значениях аргументов ; .



Вариант 12

Задание 1

Построить в разных системах координат графики функций:

при заданных значениях аргумента . Выполнить условное форматирование таблицы значений аргумента и функций, так чтобы ячейки значений в диапазонах: ;имели заливку разными цветами. Для функции определить наилучшее линейное приближение двумя способами: используя функцию ЛИНЕЙН и с помощью пункта меню Сервис | Анализ данных | Регрессия.


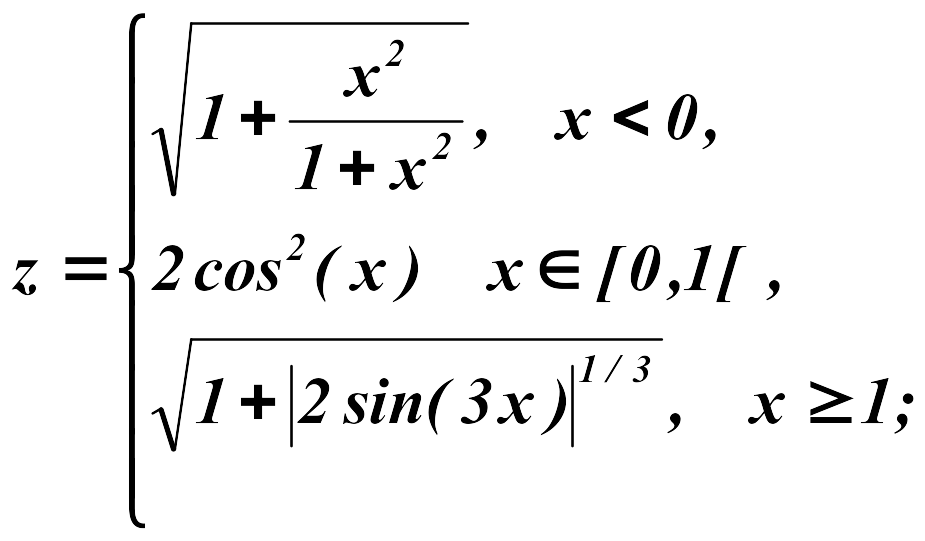
Задание 2


Построить в одной системе координат графики функций при . Вычислить определенный интеграл методом трапеций от функции


Задание 3


Построить поверхность при заданных значениях аргументов ; .



Вариант 13

Задание 1

Построить в разных системах координат графики функций:

при заданных значениях аргумента . Выполнить условное форматирование таблицы значений аргумента и функций, так чтобы ячейки значений в диапазонах: ;имели заливку разными цветами. Для функции определить наилучшее линейное приближение двумя способами: используя функцию ЛИНЕЙН и с помощью пункта меню Сервис | Анализ данных | Регрессия.


Задание 2


Построить в одной системе координат графики функций при . Вычислить определенный интеграл методом трапеций от функции

Задание 3


Построить поверхность при заданных значениях аргументов ; .


Вариант 14

Задание 1

Построить в разных системах координат графики функций:

при заданных значениях аргумента . Выполнить условное форматирование таблицы значений аргумента и функций, так чтобы ячейки значений в диапазонах: ;имели заливку разными цветами. Для функции определить наилучшее линейное приближение двумя способами: используя функцию ЛИНЕЙН и с помощью пункта меню Сервис | Анализ данных | Регрессия.


Задание 2


Построить в одной системе координат графики функций при . Вычислить определенный интеграл методом трапеций от функции

Задание 3


Построить поверхность при заданных значениях аргументов ; .



Вариант 15

Задание 1

Построить в разных системах координат графики функций:

при заданных значениях аргумента . Выполнить условное форматирование таблицы значений аргумента и функций, так чтобы ячейки значений в диапазонах: ;имели заливку разными цветами. Для функции определить наилучшее линейное приближение двумя способами: используя функцию ЛИНЕЙН и с помощью пункта меню Сервис | Анализ данных | Регрессия.


Задание 2


Построить в одной системе координат графики функций при . Вычислить определенный интеграл методом трапеций от функции


Задание 3


Построить поверхность при заданных значениях аргументов ; .


Вариант 16

Задание 1

Построить в разных системах координат графики функций:

при заданных значениях аргумента . Выполнить условное форматирование таблицы значений аргумента и функций, так чтобы ячейки значений в диапазонах: ;имели заливку разными цветами. Для функции определить наилучшее линейное приближение двумя способами: используя функцию ЛИНЕЙН и с помощью пункта меню Сервис | Анализ данных | Регрессия.


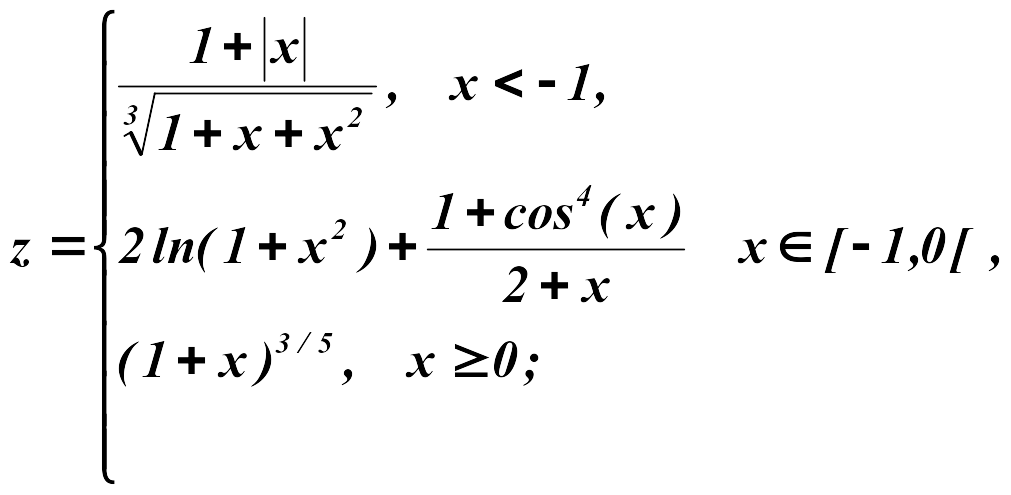
Задание 2


Построить в одной системе координат графики функций при . Вычислить определенный интеграл методом трапеций от функции


Задание 3


Построить поверхность при заданных значениях аргументов ; .




Вариант 17

Задание 1

Построить в разных системах координат графики функций:

при заданных значениях аргумента . Выполнить условное форматирование таблицы значений аргумента и функций, так чтобы ячейки значений в диапазонах: ;имели заливку разными цветами. Для функции определить наилучшее линейное приближение двумя способами: используя функцию ЛИНЕЙН и с помощью пункта меню Сервис | Анализ данных | Регрессия.


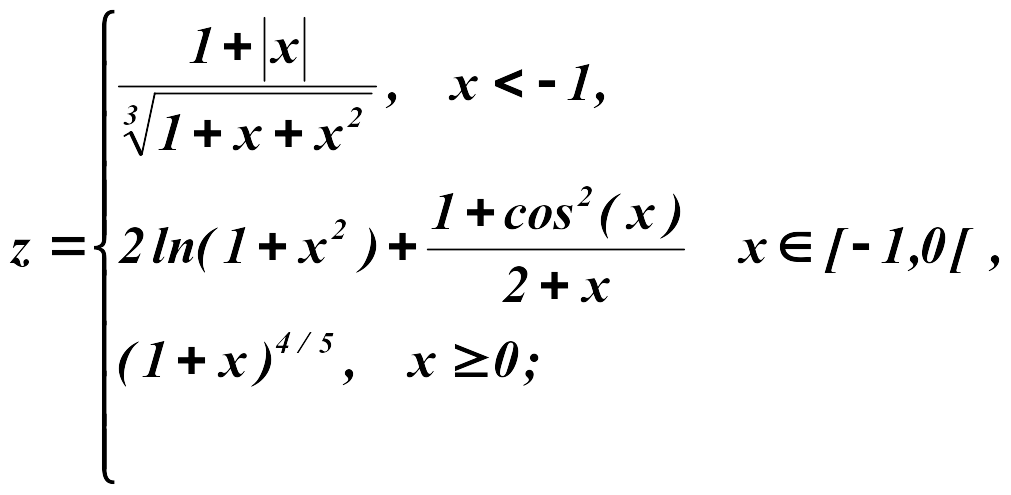
Задание 2


Построить в одной системе координат графики функций при . Вычислить определенный интеграл методом трапеций от функции


Задание 3


Построить поверхность при заданных значениях аргументов ; .



Вариант 18

Задание 1

Построить в разных системах координат графики функций:

при заданных значениях аргумента . Выполнить условное форматирование таблицы значений аргумента и функций, так чтобы ячейки значений в диапазонах: ;имели заливку разными цветами. Для функции определить наилучшее линейное приближение двумя способами: используя функцию ЛИНЕЙН и с помощью пункта меню Сервис | Анализ данных | Регрессия.


Задание 2


Построить в одной системе координат графики функций при . Вычислить определенный интеграл методом трапеций от функции


Задание 3


Построить поверхность при заданных значениях аргументов ; .



Вариант 19

Задание 1

Построить в разных системах координат графики функций:

при заданных значениях аргумента . Выполнить условное форматирование таблицы значений аргумента и функций, так чтобы ячейки значений в диапазонах: ;имели заливку разными цветами. Для функции определить наилучшее линейное приближение двумя способами: используя функцию ЛИНЕЙН и с помощью пункта меню Сервис | Анализ данных | Регрессия.


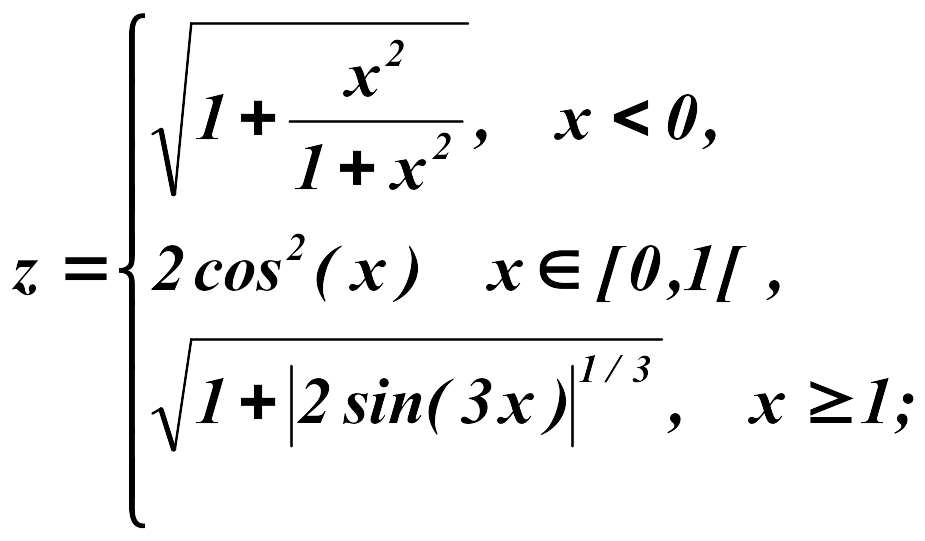
Задание 2


Построить в одной системе координат графики функций при . Вычислить определенный интеграл методом трапеций от функции


Задание 3


Построить поверхность при заданных значениях аргументов ; .



Вариант 20

Задание 1

Построить в разных системах координат графики функций:

при заданных значениях аргумента . Выполнить условное форматирование таблицы значений аргумента и функций, так чтобы ячейки значений в диапазонах: ;имели заливку разными цветами. Для функции определить наилучшее линейное приближение двумя способами: используя функцию ЛИНЕЙН и с помощью пункта меню Сервис | Анализ данных | Регрессия.


Задание 2


Построить в одной системе координат графики функций при . Вычислить определенный интеграл методом трапеций от функции


Задание 3


Построить поверхность при заданных значениях аргументов ; .


Вариант 21

Задание 1

Построить в разных системах координат графики функций:

при заданных значениях аргумента . Выполнить условное форматирование таблицы значений аргумента и функций, так чтобы ячейки значений в диапазонах: ;имели заливку разными цветами. Для функции определить наилучшее линейное приближение двумя способами: используя функцию ЛИНЕЙН и с помощью пункта меню Сервис | Анализ данных | Регрессия.


Задание 2


Построить в одной системе координат графики функций при . Вычислить определенный интеграл методом трапеций от функции


Задание 3


Построить поверхность при заданных значениях аргументов ; .



Вариант 22

Задание 1

Построить в разных системах координат графики функций:

при заданных значениях аргумента . Выполнить условное форматирование таблицы значений аргумента и функций, так чтобы ячейки значений в диапазонах: ;имели заливку разными цветами. Для функции определить наилучшее линейное приближение двумя способами: используя функцию ЛИНЕЙН и с помощью пункта меню Сервис | Анализ данных | Регрессия.

Задание 2


Построить в одной системе координат графики функций при . Вычислить определенный интеграл методом трапеций от функции

Смотрите также файлы