Добавлен: 15.11.2018
Просмотров: 1438
Скачиваний: 6
![]()
![]()
Задание 3
Построить
поверхность
![]() при заданных значениях аргументов
при заданных значениях аргументов
![]() ;
;
![]() .
.
![]()
Вариант 23
Задание 1
Построить в разных системах координат графики функций:
![]() при
заданных значениях аргумента
при
заданных значениях аргумента
![]() .
Выполнить условное форматирование
таблицы значений аргумента и функций,
так чтобы ячейки значений в диапазонах:
.
Выполнить условное форматирование
таблицы значений аргумента и функций,
так чтобы ячейки значений в диапазонах:
![]() ;
;![]() имели
заливку разными цветами. Для функции
имели
заливку разными цветами. Для функции
![]() определить наилучшее линейное приближение
определить наилучшее линейное приближение
![]() двумя способами: используя функцию
ЛИНЕЙН и с помощью пункта меню Сервис
| Анализ
данных |
Регрессия.
двумя способами: используя функцию
ЛИНЕЙН и с помощью пункта меню Сервис
| Анализ
данных |
Регрессия.
![]()
![]()
![]()
Задание 2
Построить
в одной системе координат графики
функций
![]() при
при
![]() .
Вычислить определенный интеграл методом
трапеций от функции
.
Вычислить определенный интеграл методом
трапеций от функции
![]()
![]()
![]()
Задание 3
Построить
поверхность
![]() при заданных значениях аргументов
при заданных значениях аргументов
![]() ;
;
![]() .
.
![]()
Вариант 24
Задание 1
Построить в разных системах координат графики функций:
![]() при
заданных значениях аргумента
при
заданных значениях аргумента
![]() .
Выполнить условное форматирование
таблицы значений аргумента и функций,
так чтобы ячейки значений в диапазонах:
.
Выполнить условное форматирование
таблицы значений аргумента и функций,
так чтобы ячейки значений в диапазонах:
![]() ;
;![]() имели
заливку разными цветами. Для функции
имели
заливку разными цветами. Для функции
![]() определить наилучшее линейное приближение
определить наилучшее линейное приближение
![]() двумя способами: используя функцию
ЛИНЕЙН и с помощью пункта меню Сервис
| Анализ
данных |
Регрессия.
двумя способами: используя функцию
ЛИНЕЙН и с помощью пункта меню Сервис
| Анализ
данных |
Регрессия.
![]()
![]()

Задание 2
Построить
в одной системе координат графики
функций
![]() при
при
![]() .
Вычислить определенный интеграл методом
трапеций от функции
.
Вычислить определенный интеграл методом
трапеций от функции
![]()
![]()
![]()
Задание 3
Построить
поверхность
![]() при заданных значениях аргументов
при заданных значениях аргументов
![]() ;
;
![]() .
.
![]()
Вариант 25
Задание 1
Построить в разных системах координат графики функций:
![]() при
заданных значениях аргумента
при
заданных значениях аргумента
![]() .
Выполнить условное форматирование
таблицы значений аргумента и функций,
так чтобы ячейки значений в диапазонах:
.
Выполнить условное форматирование
таблицы значений аргумента и функций,
так чтобы ячейки значений в диапазонах:
![]() ;
;![]() имели
заливку разными цветами. Для функции
имели
заливку разными цветами. Для функции
![]() определить наилучшее линейное приближение
определить наилучшее линейное приближение
![]() двумя способами: используя функцию
ЛИНЕЙН и с помощью пункта меню Сервис
| Анализ
данных |
Регрессия.
двумя способами: используя функцию
ЛИНЕЙН и с помощью пункта меню Сервис
| Анализ
данных |
Регрессия.
![]()
![]()
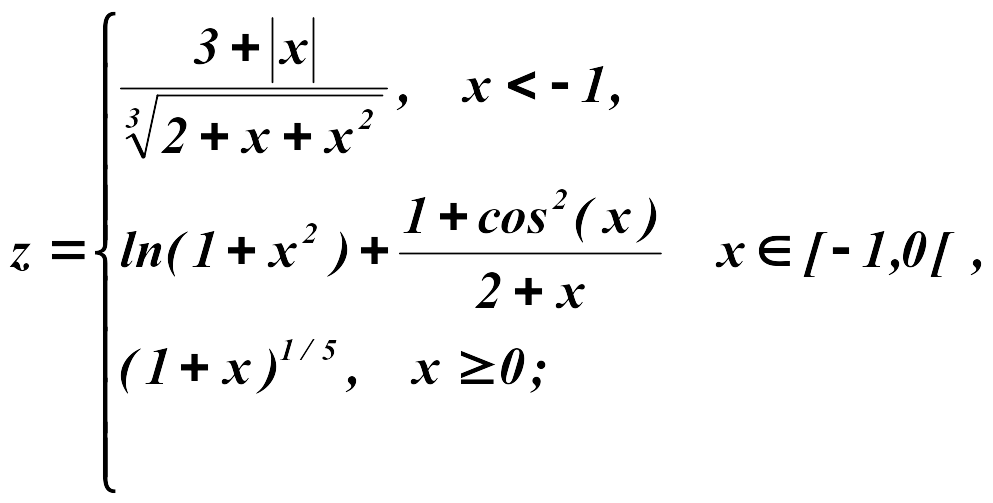
Задание 2
Построить
в одной системе координат графики
функций
![]() при
при
![]() .
Вычислить определенный интеграл методом
трапеций от функции
.
Вычислить определенный интеграл методом
трапеций от функции
![]()
![]()
![]()
Задание 3
Построить
поверхность
![]() при заданных значениях аргументов
при заданных значениях аргументов
![]() ;
;
![]() .
.
![]()
Вариант 26
Задание 1
Построить в разных системах координат графики функций:
![]() при
заданных значениях аргумента
при
заданных значениях аргумента
![]() .
Выполнить условное форматирование
таблицы значений аргумента и функций,
так чтобы ячейки значений в диапазонах:
.
Выполнить условное форматирование
таблицы значений аргумента и функций,
так чтобы ячейки значений в диапазонах:
![]() ;
;![]() имели
заливку разными цветами. Для функции
имели
заливку разными цветами. Для функции
![]() определить наилучшее линейное приближение
определить наилучшее линейное приближение
![]() двумя способами: используя функцию
ЛИНЕЙН и с помощью пункта меню Сервис
| Анализ
данных |
Регрессия.
двумя способами: используя функцию
ЛИНЕЙН и с помощью пункта меню Сервис
| Анализ
данных |
Регрессия.
![]()
![]()
![]()
Задание 2
Построить
в одной системе координат графики
функций
![]() при
при
![]() .
Вычислить определенный интеграл методом
трапеций от функции
.
Вычислить определенный интеграл методом
трапеций от функции
![]()
![]()
![]()
Задание 3
Построить
поверхность
![]() при заданных значениях аргументов
при заданных значениях аргументов
![]() ;
;
![]() .
.
![]()
Вариант 27
Задание 1
Построить в разных системах координат графики функций:
![]() при
заданных значениях аргумента
при
заданных значениях аргумента
![]() .
Выполнить условное форматирование
таблицы значений аргумента и функций,
так чтобы ячейки значений в диапазонах:
.
Выполнить условное форматирование
таблицы значений аргумента и функций,
так чтобы ячейки значений в диапазонах:
![]() ;
;![]() имели
заливку разными цветами. Для функции
имели
заливку разными цветами. Для функции
![]() определить наилучшее линейное приближение
определить наилучшее линейное приближение
![]() двумя способами: используя функцию
ЛИНЕЙН и с помощью пункта меню Сервис
| Анализ
данных |
Регрессия.
двумя способами: используя функцию
ЛИНЕЙН и с помощью пункта меню Сервис
| Анализ
данных |
Регрессия.
![]()
![]()

Задание 2
Построить
в одной системе координат графики
функций
![]() при
при
![]() .
Вычислить определенный интеграл методом
трапеций от функции
.
Вычислить определенный интеграл методом
трапеций от функции
![]()
![]()
![]()
Задание 3
Построить
поверхность
![]() при заданных значениях аргументов
при заданных значениях аргументов
![]() ;
;
![]() .
.
![]()
Вариант 28
Задание 1
Построить в разных системах координат графики функций:
![]() при
заданных значениях аргумента
при
заданных значениях аргумента
![]() .
Выполнить условное форматирование
таблицы значений аргумента и функций,
так чтобы ячейки значений в диапазонах:
.
Выполнить условное форматирование
таблицы значений аргумента и функций,
так чтобы ячейки значений в диапазонах:
![]() ;
;![]() имели
заливку разными цветами. Для функции
имели
заливку разными цветами. Для функции
![]() определить наилучшее линейное приближение
определить наилучшее линейное приближение
![]() двумя способами: используя функцию
ЛИНЕЙН и с помощью пункта меню Сервис
| Анализ
данных |
Регрессия.
двумя способами: используя функцию
ЛИНЕЙН и с помощью пункта меню Сервис
| Анализ
данных |
Регрессия.
![]()
![]()
![]()
Задание 2
Построить
в одной системе координат графики
функций
![]() при
при
![]() .
Вычислить определенный интеграл методом
трапеций от функции
.
Вычислить определенный интеграл методом
трапеций от функции
![]()
![]()
![]()
Задание 3
Построить
поверхность
![]() при заданных значениях аргументов
при заданных значениях аргументов
![]() ;
;
![]() .
.
![]()
Вариант 29
Задание 1
Построить в разных системах координат графики функций:
![]() при
заданных значениях аргумента
при
заданных значениях аргумента
![]() .
Выполнить условное форматирование
таблицы значений аргумента и функций,
так чтобы ячейки значений в диапазонах:
.
Выполнить условное форматирование
таблицы значений аргумента и функций,
так чтобы ячейки значений в диапазонах:
![]() ;
;![]() имели
заливку разными цветами. Для функции
имели
заливку разными цветами. Для функции
![]() определить наилучшее линейное приближение
определить наилучшее линейное приближение
![]() двумя способами: используя функцию
ЛИНЕЙН и с помощью пункта меню Сервис
| Анализ
данных |
Регрессия.
двумя способами: используя функцию
ЛИНЕЙН и с помощью пункта меню Сервис
| Анализ
данных |
Регрессия.
![]()
![]()
![]()
Задание 2
Построить
в одной системе координат графики
функций
![]() при
при
![]() .
Вычислить определенный интеграл методом
трапеций от функции
.
Вычислить определенный интеграл методом
трапеций от функции
![]()
![]()
![]()
Задание 3
Построить
поверхность
![]() при заданных значениях аргументов
при заданных значениях аргументов
![]() ;
;
![]() .
.
![]()
Вариант 30
Задание 1
Построить в разных системах координат графики функций:
![]() при
заданных значениях аргумента
при
заданных значениях аргумента
![]() .
Выполнить условное форматирование
таблицы значений аргумента и функций,
так чтобы ячейки значений в диапазонах:
.
Выполнить условное форматирование
таблицы значений аргумента и функций,
так чтобы ячейки значений в диапазонах:
![]() ;
;![]() имели
заливку разными цветами. Для функции
имели
заливку разными цветами. Для функции
![]() определить наилучшее линейное приближение
определить наилучшее линейное приближение
![]() двумя способами: используя функцию
ЛИНЕЙН и с помощью пункта меню Сервис
| Анализ
данных |
Регрессия.
двумя способами: используя функцию
ЛИНЕЙН и с помощью пункта меню Сервис
| Анализ
данных |
Регрессия.
![]()
![]()
![]()
Задание 2
Построить
в одной системе координат графики
функций
![]() при
при
![]() .
Вычислить определенный интеграл методом
трапеций от функции
.
Вычислить определенный интеграл методом
трапеций от функции
![]()
![]()
![]()
Задание 3
Построить
поверхность
![]() при заданных значениях аргументов
при заданных значениях аргументов
![]() ;
;
![]() .
.
![]()
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
1. Информатика: Базовый курс / С.В. Симонович и др. - СПб.: Питер, 2003. - 640 с.: ил.
2. Информатика: Практикум по технологии работы на компьютере / под ред. Н.В. Макаровой. - 3-е изд., перераб. - М.: Финансы и статистика, 2004. - 256 с.: ил.
3. Информатика: Учебник / Под ред. Н.В. Макаровой. - 3-е изд., пере раб. - М.: Финансы и статистика, 2004. - 768 с.: ил.
4. Информатика: Учебник для вузов/ В.А. Острейковский. - М.: Высш. шк., 2001.
Дополнительная литература
1. Информатика для юристов и экономистов / С.В. Симонович и др. - СПб.: Питер, 2004.-688 с.: ил.
2. Новейшая энциклопедия персонального компьютера./ В.П. Леонтьева - М.: ОЛМА-ПРЕСС Образование, 2004. - 734 с.: ил.