2 Методические указания по решению практической задачи

Пример выполнения задания

Задание 1

Построить в разных системах координат графики функций:

при заданных значениях аргумента . Выполнить условное форматирование таблицы значений аргумента и функций, так чтобы ячейки значений в диапазонах: ;имели заливку разными цветами. Для функции определить наилучшее линейное приближение двумя способами: используя функцию ЛИНЕЙН и с помощью пункта меню Сервис | Анализ данных | Регрессия.

Дано:

а)

б)

в)

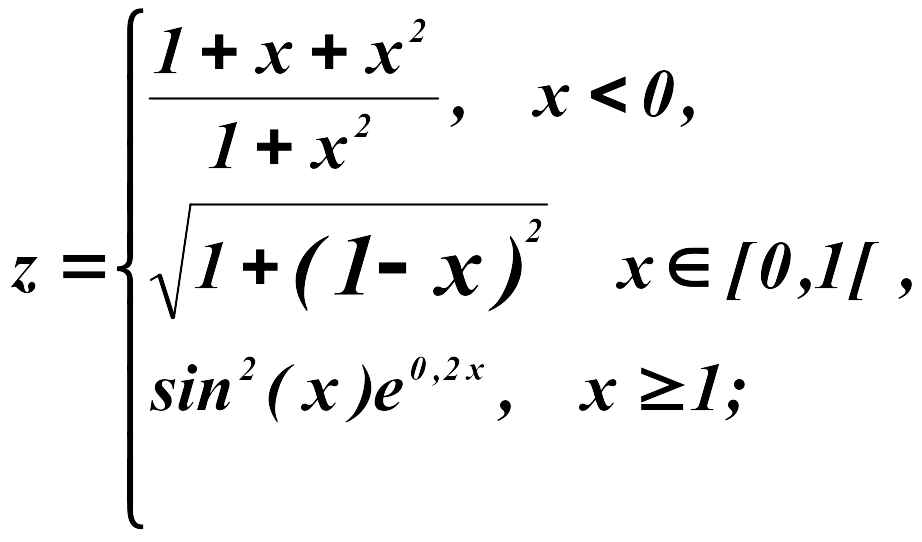
Решение

Для решения задачи понадобится функция =ЕСЛИ(логическое_выражение; значение_если_истина; значение_если_ложь).

Рисунок 1. Фрагмент таблицы 1 с формулами

Определение наилучшего линейного приближения функции связано с вычислением коэффициентов в уравнении прямой методом наименьших квадратов по заданному набору аргумента и значений функции . Для этого:

1. Сделайте текущей ячейку N1 и щелкните на кнопке Вставка функции в строке формул.

2. В окне мастера функции выберите категорию Ссылки и массивы и функцию ИНДЕКС. В новом диалоговом окне выберите первый вариант набора параметров.

3. Установите текстовый курсор в первое поле для ввода параметров Аргументы функции и выберите в раскрывающемся списке в строке формул пункт Другие функции.

4. С помощью мастера функций выберите функцию ЛИНЕЙН категории Статистические.

5. В качестве первого параметра функции ЛИНЕЙН выберите диапазон, содержащий значения функции .

6. В качестве второго параметра функции ЛИНЕЙН выберите диапазон, содержащий значения независимой переменной .

7. Переместите текстовый курсор в строке формул, чтобы он стоял на имени функции ИНДЕКС. В качестве второго параметра функции ИНДЕКС задайте число 1. Щелкните на кнопке ОК в окне Аргументы функции.

Функция ЛИНЕЙН возвращает коэффициенты уравнения прямой в виде массива из двух элементов. С помощью функции ИНДЕКС выбирается нужный элемент.

8. Сделайте текущей ячейку N2. Повторите операции пунктов 1...7, чтобы в ячейке в итоге появилась формула =ИНДЕКС(ЛИНЕЙН($D$3:$D$33;$A$3:$A$33);2). Ее можно ввести и по­символьно.

В ячейках N1, N2 вычислены соответственно коэффициенты в уравнении прямой по первым тридцати точкам.

Для построения наилучшей прямой другим способом необходимо:

1. Дать команду Сервис | Анализ данных.

2. В списке Инструменты анализа выбрать пункт Регрессия.

3. В поле Входной интервал Y указать методом протягивания диапазон значений функции (не более 30).

4. В поле Входной интервал X указать методом протягивания диапазон значений аргумента функции.

5. Установить переключатель Новый рабочий лист и задать для него имя Регрессия 1(а).

6. Щелкнуть на кнопке ОК и по окончании расчетов откроется рабочий лист Регрессия 1(а). Убедитесь, что вычисленные коэффициенты обоими способами совпадают.

Таблица 1 Результат выполнения задания 1(а)

Используя полученные данные, построим график функции у(x)

Рисунок 2. График функции y(x)

Используя полученные данные, построим график функции g(x)

Рисунок 3. График функции g(x)

Используя полученные данные, построим график функции z(x)

Рисунок 3. График функции z(x)

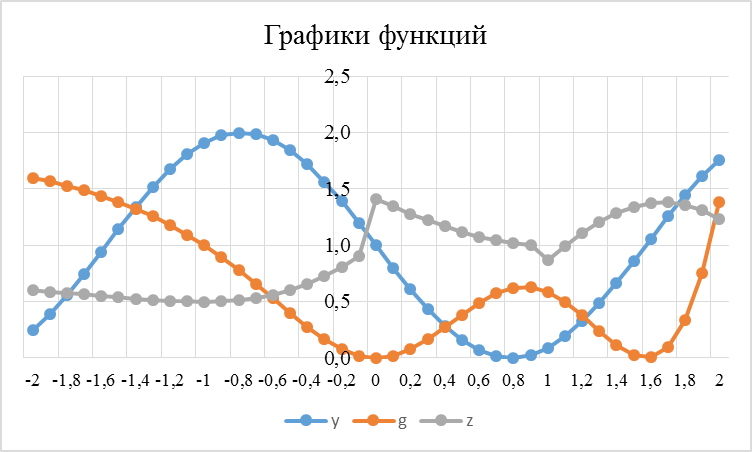
Рисунок 4. Графики функций у(х), g(x) и z(x)

2. Для построения наилучшей прямой другим способом необходимо:

1. Дать команду Сервис | Анализ данных.

2. В списке Инструменты анализа выбрать пункт Регрессия.

3. В поле Входной интервал Y указать методом протягивания диапазон значений функции (не более 30).

4. В поле Входной интервал X указать методом протягивания диапазон значений аргумента функции.

5. Установить переключатель Новый рабочий лист и задать для него имя Регрессия 1(а).

6. Щелкнуть на кнопке ОК и по окончании расчетов откроется рабочий лист Регрессия 1(а). Убедитесь, что вычисленные коэффициенты обоими способами совпадают.

Решение

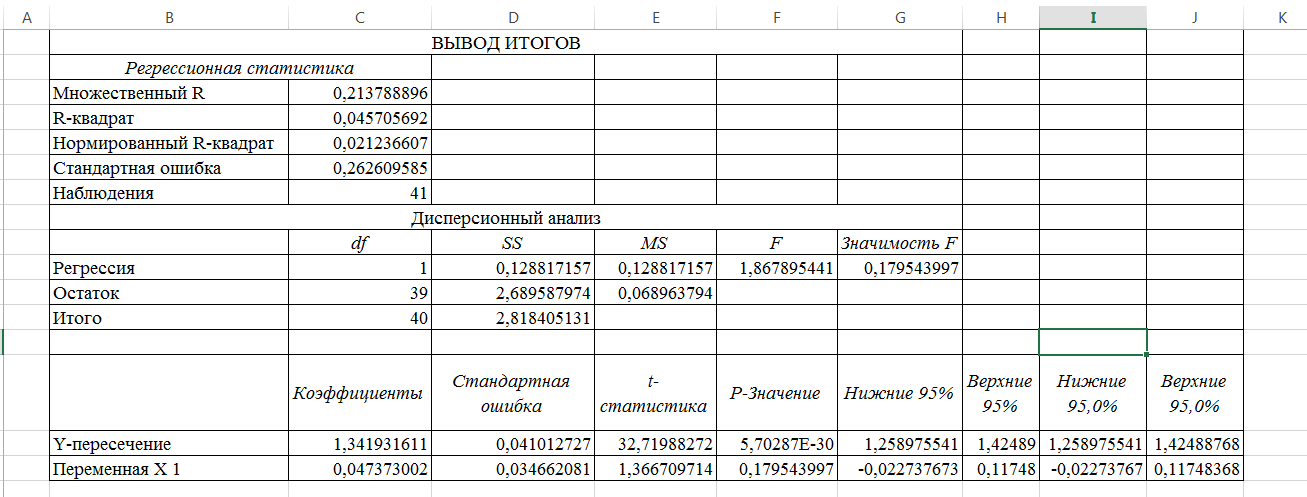
Рисунок 5. Регрессия. Вывод итогов

Уравнение линейной зависимости имеет вид: y(x)=0,0474x+1,342

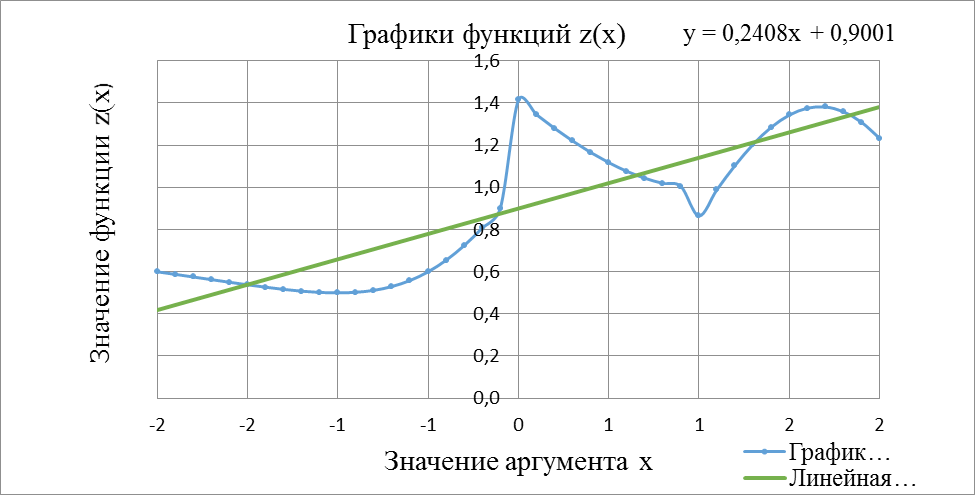
Рисунок 6. График функции z(x) и линейного приближения

Задание 2

Построить в одной системе координат графики функций при . Вычислить определенный интеграл методом трапеций от функции

Решение

При вычислении определенного интеграла от воспользуемся формулой трапеций:

; где - шаг интегрирования.

Для суммирования возможно использовать кнопку Автосумма на стандартной панели.

Заполняем лист Excel следующим образом:

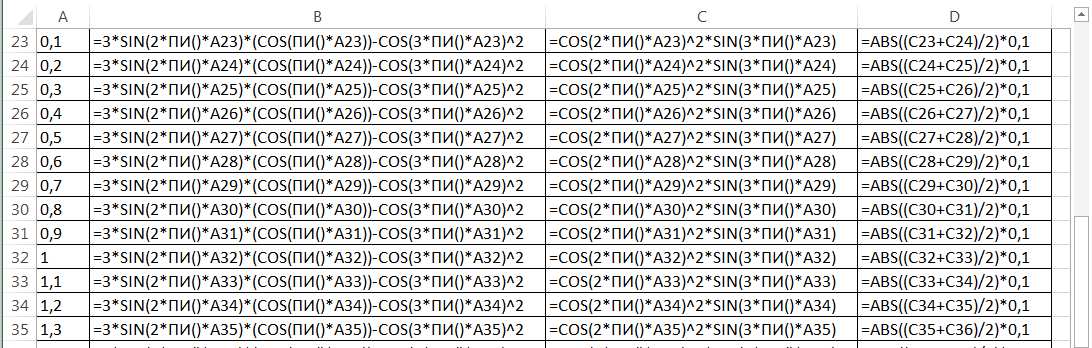
Рисунок 6. Фрагмент таблицы 2 с формулами

Таблица 2. Табулирование функции

Используя полученные данные, построим графики функций

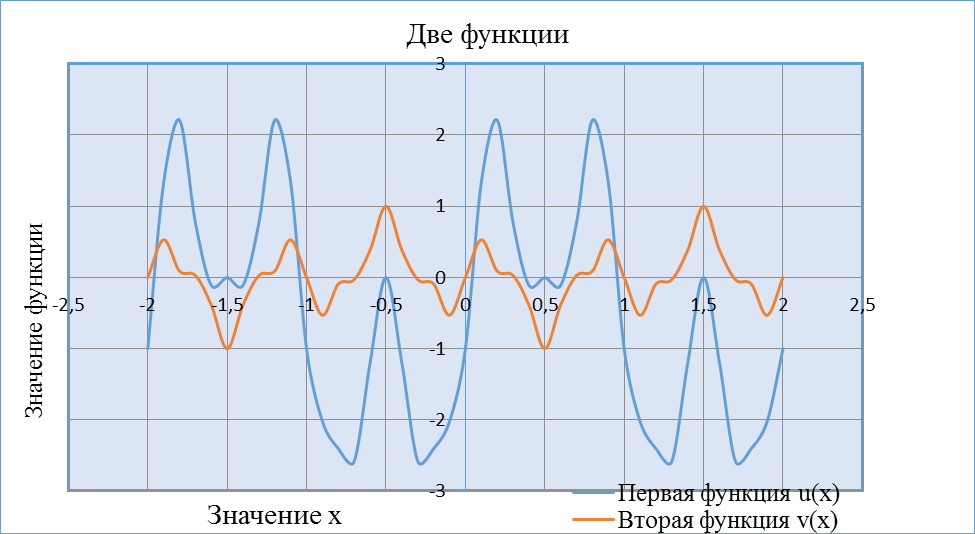
Рисунок 7. График функций

Задание 3

Построить поверхность при заданных значениях аргументов ; .

Решение

Построение поверхности в задании 3 сопровождается заполнением двумерного массива в таблице с пустой ячейкой в левом верхнем углу, значениями переменной в крайнем левом столбце и значениями переменной в верхней строке массива. Остальные ячейки заполняются формулами со смешанным типом ссылок (для удобства автозаполнения), например в ячейке F20 записано =3*$A20^3*SIN($A20)-2*COS(F$2). Перед построением поверхности с помощью Мастера диаграмм удобно выделить прямоугольную область таблицы с пустой верхней левой ячейкой.

Результат выполнения задания 3

Фрагмент таблицы

Поверхность

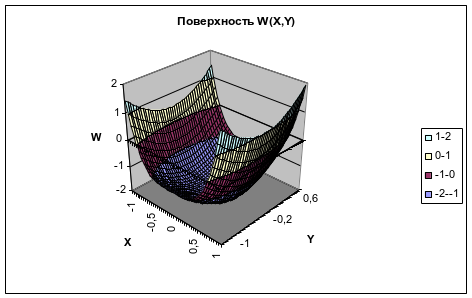
Рисунок 8. График поверхности