1. Пропорции. Золотое сечение.

Знание пропорций, т.е. соотношений размеров частей человеческой фигуры, необходимо для правильного изображения человека и неудивительно, что этим всегда занимались художники и анатомы. Под пропорцией понимается соотношение частей целого между собой и этим целым. В математике пропорцией называют равенство двух отношений а : в = с : д

В эпоху Ренессанса среднепропорциональное отношение называли Божественной пропорцией. Леонардо да Винчи дает ей название «золотое сечение».

П

Рис.1.1. Доска-панель из склепа

Хеси-Ра. Древнее царство.18 век до н.э.

ХХеси-О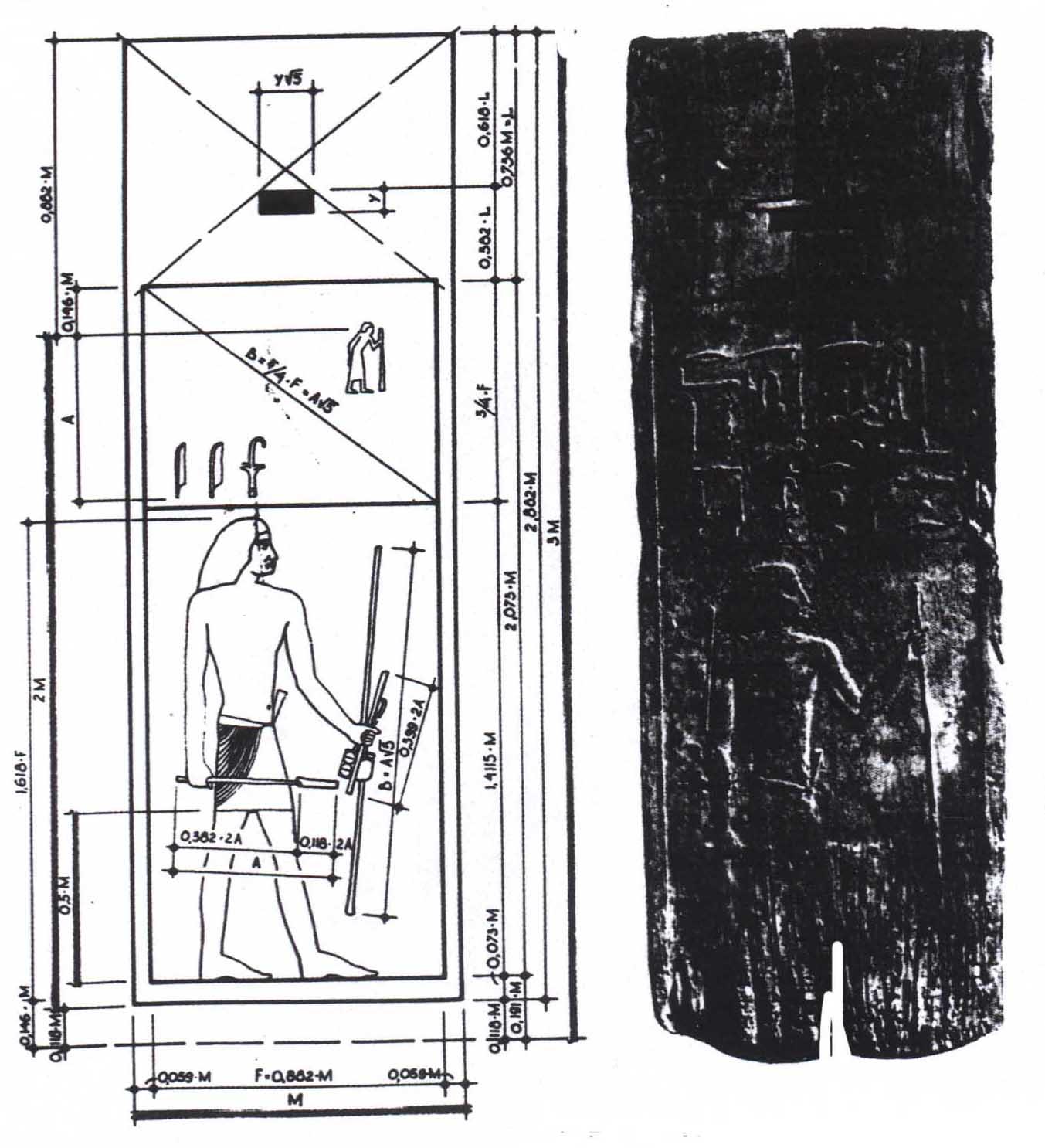

ринято считать, что понятие о золотом сечении ввел в научный обиход Пифагор. Есть предположение, что Пифагор заимствовал знания у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзье нашел, что в рельефе из храма фараона Сети 1 в Абидосе и в рельефе Рамзеса, пропорции фигур соответствуют величинам золотого сечения. Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени(рис.1.1.), держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого сечения. О золотом делении знали Платон, Евклид, Гипсикл, Папп и др.

С открытием в 1202 году ряда Фибоначчи было обнаружено основное свойство золотого сечения – единство аддитивности и мультикативности. В математике понятие «аддитивность» означает, что в числовом ряду Ф1,Ф2, Ф3,Ф3,Ф4, Фn-1,Фn, каждый последующий член равен сумме двух предыдущих. Причем за начало такого ряда можно принять любые два числа, например 0 и 1, 1и 3 и т.д. Мультикативность означает, что в числовом ряду Ф1,Ф2, Ф3,Ф3,Ф4, Фn-1,Фn все члены ряда связаны в геометрическую прогрессию Ф1:Ф2 = Ф2:Ф3 = Ф3:Ф4… Фn-1:Фn =const.

Число золотого сечения, соединяющее свойства аддитивности и мультикативности, находится как общий корень двух уравнений:

а+в=с (аддитивность)

а : в = в : с (мультикативность).

Числа, образующие последовательность 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, ... называются "числами Фибоначчи", а сама последовательность - последовательностью Фибоначчи. В числах Фибоначчи существует одна очень интересная особенность. При делении любого числа из последовательности на число, стоящее перед ним в ряду, результатом всегда будет величина, колеблющаяся около иррационального значения 1.61803398875... и через раз то пpевосходящая, то не достигающая его.
(Прим. иррациональное число, т.е. число, десятичное представление которого бесконечно и не периодично).

Более того, после 13-ого числа в последовательности этот результат деления становится постоянным до бесконечности ряд. Именно это постоянное число деления в средние века было названо Божественной пропорцией, а ныне в наши дни именуется как золотое сечение, золотое сpеднее или золотая пропорция. В алгебpе это число обозначается гpеческой буквой фи (Ф)

---

Итак, Золотая пропорция = 1 : 1,618

В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением как в геометрии, так и в искусстве, особенно в архитектуре Леонардо да Винчи.

В 1496 году по приглашению герцога Моро в Милан приезжает математик Лука Пачоли. В то же время при дворе Моро работал и Леонардо да Винчи. В 1509 году в Венеции была издана книга
Луки Пачоли «Божественная пропорция» с блестяще выполненными иллюстрациями, ввиду чего полагают, что их сделал Леонардо да Винчи. Книга была восторженным гимном золотой пропорции. Среди многих достоинств золотой пропорции Лука Пачоли не преминул назвать и ее «божественную суть» как выражение божественного триединства: бог сын, бог отец и бог святой дух.

Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название золотое сечение. Золотое сечение - это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему. В математике пропорцией называют равенство двух отношений: a:b=c:d.
Отрезок прямой АВ можно разделить точкой C на две части следующими способами:
на две равные части АВ : АC = АВ : ВC;
на две неравные части в любом отношении (такие части пропорции не образуют);
таким образом, когда АВ : АC = АC : ВC.
Последнее и есть золотое деление или деление отрезка в крайнем и среднем отношении.

Золотое сечение - это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему
a : b = b : c или с : b = b : а.

П остроим отрезки в пропорциях золотого сечения. В прямоугольнике с соотношением сторон 1:2 проводится диагональ, на которую поворотом накладывается меньшая сторона. Остаток диагонали поворачивается вокруг вершины прямоугольника до совмещения с положением верхнего основания. Таким образом, верхнее основание поделилось на два неравных отрезка в пропорции золотого сечения.

З

Рис.1.2. Распространение золотого сечения.

ХХеси-О

олотое сечение распространено очень широко – как числовая характеристика членения стеблей растений, их расположения на стволе, закручивания спиралей подсолнечника, строение раковины, яйца, яблока и конечно, описание пропорций человеческого тела (рис.1.2.)

Известно, что скульптура Поликлета «Дорифор» вплоть до мельчайших деталей построена в пропорции золотого сечения (рис.1.3.)

---

В 20 веке Ле Корбюзье для применения в плоскостных и объемных композициях, создал «модулер» (рис.1.4.) « Модулер – мерило, основанное на сочетании математики и человеческого масштаба; оно состоит из двух рядов числовых величин – красного и синего ряда. Можно ли ограничится одной числовой таблицей? Нет. И мне вновь хочется пояснить весь комплекс идей, положенных в основу изобретения. Метр – это условная в еличина…Сущность изобретения была выражена с редкой простотой: «модулер» - это средство измерения, основой которого являются рост человека и математика. Человек с поднятой рукой дает нам точки, определяющие занятое пространство - нога, солнечное сплетение, голова, кончик пальцев поднятой руки – три интервала, обуславливающие серию золотого сечения, называемую радом Фибоначчи. С другой стороны, математика предлагает некоторое и

Рис.1.3. Скульптура Поликлета «Дорифор»

ХХеси-О

зменение: простой квадрат, удвоение и два золотых сечения»

Вот вкратце основные позиции модулера:

«1. Наша решетка дате три размера:113, 70, 43 ( в см), которые согласуются с Ф ( золотое сечение) и рядом Фибоначчи:43+70=113 или 113-70=43. В сумме они дают: 113+70=183, 113+70+43=226

2. Эти три размера – 113, 183, 226 - определяют величину пространства, занимаемого человеком шести футов.

3. Размер 113 определяет золотое сечение 70, показывая начало первой, красной серии 4-6-10-16-27-43-70-113-183-226 и т.д. До сих пор, стоящий человек служил определению трех, а не четырех решающих значений модулера, а именно: 113 – солнечное сплетение, 182 –вершина головы, 226 – конец пальцев поднятой руки. Второе отношение Ф, 140-86, вводит четвертую существенную точку фигуры человека – точку опоры опущенной руки: 86 см. Таким образом, если человек, у которого левая рука понята, а правая непринужденно опущена, то она даст отметку 86. В результате мы получаем четыре точки, определяющие с помощью фигуры человека занимаемое им пространство. Размер 226 (2х113 –удвоение) определяет золотое сечение 140-86, показывая начало второй, голубой, серии: 13-20,3 -33-53-86-140-226-366-592 и т.д.

4. Из этих значений и размеров отметим те, которые определенно связаны с ростом человека…»

 Практические задания

1. Постройте посредством циркуля и линейки два отрезка в пропорциях золотого сечения. Затем меньший из них опять поделите в пропорции Ф (золотого сечения) на два отрезка и т.д.

2. Возьмите рисунок скульптуры Поликлета. Попробуйте составить схему пропорционирования.

3. П ользуясь рис.1.4. «Золотые пропорции в частях тела человека и фигуры человека» докажите свойства золотого сечения.

Рис.1.4.Золотые пропорции в частях тела человека и фигуры человека

ХХеси-О

 Вопросы для самоконтроля и взаимного контроля

1. Дайте определение золотого сечения.

2. Кто ввел понятие о золотом делении?

3. Какой вклад внес Леонардо да Винчи в разработку вопроса о золотом сечении?

4. По мнению Луки Пачоли золотая пропорция содержит «божественную суть». В чем она заключается?

5. В чем состоит основное свойство золотого сечения?

6. Каково назначение «модулера» Корбюзье?

7. Приведите примеры как и где проявляет себя золотое сечение? В природе, архитектуре, промышленности? (по возможности подобрать рисунки и проиллюстрировать)

---

2. Пропорции фигуры человека

Канон – система идеальных пропорций человеческого тела. Понятие канон ввел немецкий художник Альбрехт Дюрер (1471-1528). Производилось измерение отдельных частей фигуры (головы, бедер, стоп и т.д.) у различных людей и выводились средние данные как размеров, так и соотношений их между собой. Например, ученый Ланге собрал сведения о росте миллиона мужчин и установил, что из них 300000 имели средний рост 165 см, 400000 – 175 см, а еще 300000 были более высокого роста. Но многие художники и анатомы не довольствовались тем, что давала природы, и подгоняли фактический материал под собственные вкусы, создавая каноны. Всего канонов было выработано около 100. Искусственность и надуманность большинства канонов не соответствует реалистическому восприятию, поэтому следует рассмотреть твердую анатомическую основу, без изменений, которые могут возникнуть под влиянием среды или индивидуальных вкусов.

1. Постоянные анатомические пропорции взрослого человека.

Длина позвоночника мало отличается у людей высокого и малого роста: высокий и низкий человек, сидя рядом, часто выглядят людьми одно роста, так как разница в росте достигается за счет длины ног.

Плечевая кость всегда длине костей предплечья, а предплечье – длиннее кисти. На руке, согнутой в локте, плечо кажется длиннее, так как его рабочая длина увеличивается на толщину локтевой кости. Локоть на свободно опущенной и согнутой в локте руке часто находится на уровне подвздошного гребня.

Бедренная кость всегда длиннее костей голени, а голень длиннее стопы. Длина бедренной кости равна длине голени плюс высота стопы. При согнутом колене на сидящей фигуре длина бедра воспринимается вместе с тазом, а высота голени со стопой еще увеличивается за счет толщины нижнего конца бедра.

Рука, опущенная вдоль стоящей фигуры, достигает концами пальцев середины бедра. Сзади ноги кажутся короче, так как зрительно воспринимаются от ягодиц.

Кисти и стопы у людей одного и того же роста могут быть самых различных размеров. Часто бывают случаи, когда у людей высоких кисти и стопы малы, а у низких – велики. Величина кистей и стоп подвергается числу наибольших вариаций.

2. Постоянные различия в пропорциях мужской и женской фигур.

Средний рост женщины меньше мужского. Высота лицевой части головы у мужчин больше мозговой; у женщин высота мозговой и лицевой части головы одинакова. Руки и в особенности ноги относительно всего роста у женщин короче, чем у мужчин.

Таз женщины относительно роста шире, чем у мужчин, а плечи уже.

У женщин, относительно ее фигуры, шея более тонкая и длинная, чем у мужчины, гортань выступает меньше и более округлая. Поясница изогнута более вперед, ягодицы выступают значительно сильнее назад. Грудная клетка на женской фигуре соответственно уже и короче по сравнению с мужской, а живот длиннее.

---

При равных условиях развития и существования у женщин меньше развиты скелет и мускулатура, жировая ткань отлагается в большем количестве и более равномерно распределена. Вследствие этого женская фигура имеет более округлые формы.

Обычно за единицу измерения человеческого тела принимается модуль – длина головы. Рост человека приблизительно равен 7 – 7,5 длин головы. Однако такие факторы, как раса, пол, возраст, индивидуальные различия в физиологии не позволяют принять какие – либо жесткие правила в отношении пропорций. Большинство художников предпочитают изображать фигуру человека с соотношением длины головы к общему росту 1:8. Иногда встречаются женщины с такими пропорциями, что это соотношение составляет 1:6. В наше время встречается соотношение и 1:7, 1:7,5, 1:8, 1:9. (см. Приложение)

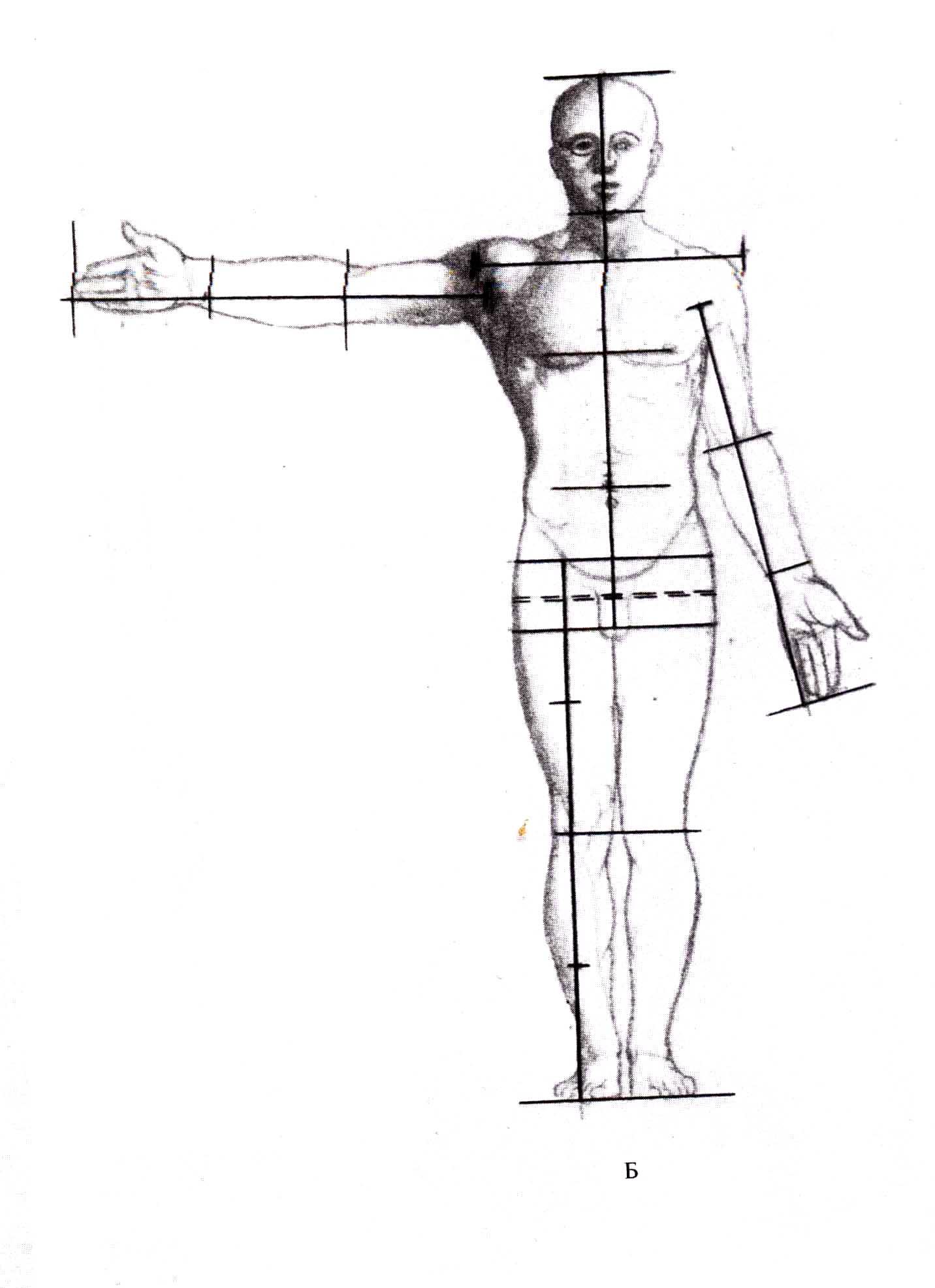
Рассмотрим пропорции фигуры человека в соотношении 1:7.

Голова, взятая за единицу измерения (модуль), укладывается по высоте 7 раз. Серединой вертикально стоящей фигуры является лонное сращение – лобок, делящий ее на две равные части (верхнюю и нижнюю).

Нижняя конечность делится по коленному суставу пополам – бедро равно голени вместе со стопой.

Расстояние от лобка до яремной ямки несколько больше длины бедра, голени со стопой. Таким образом, эти три размера легко сравнивать между собой.

Верхняя конечность, от акромиального отростка лопатки до первого сустава указательного пальца, равна четырем размерам головы. Плечо, от акромиального отростка до локтевого сустава, равно полуторным размерам головы и расстоянию от яремной ямки до талии (или пупка). Опущенная рука равно трем головам. Средний палец кисти достигает до середины бедра. На боковой поверхности (в профиль) серединой фигуры является большой вертел бедра. А на задней поверхности – нижняя точка крестца, делящая фигуру пополам.

Голень со стопой равны двум головам; бедро (от коленного сустава до большого вертела) также равно двум головам. Такими образом, в длине нижней конечности укладывается четыре размера головы.

Определив крупные пропорциональные соотношения, переходят к поискам деталей. Так, длина кисти равна расстоянию от подбородочных возвышений нижней челюсти до лобных бугров. Длина шеи со спины равна длине ключицы и высоте лопатки. Длина позвоночного столба (от первого шейного позвонка до крестца) составляет четыре размера длины кисти руки.

Ф

Рис.2.1. Пропорции фигуры 1:7,5

ХХеси-О

ранцузский анатом Рише приводит в своих ценных работах многочисленные измерения. Он установил закон о 7 1/2 – кратной длине головы (рис.2.1) Начиная сверху, нужно на теле отмерить на теле четыре раза длину головы. Измерение пятой единицы следует начинать выше на половину длины головы, таким образом, длина всего тела будет равняться не восьмикратной длине тела, а 7 1\2-кратной, то есть она будет на половину длины головы короче. Измерение верхней конечности начинают с фаланг. Длина головы соответствует длине кисти и лучезапястного сустава. Длина кисти соответствует трем четвертям длины головы. Центром при этом измерении служит точка тыльной стороны кисти, находящаяся над головкой третьей пястной кости.

---

Смотрите также файлы

• Текст пособия.doc

• СТП-1596 КП.doc

• Цельный текст.doc

• Положение детского Конкурса.doc

• LAB4.doc