Файл: Мультипроцессоры (ТЕОРЕТИЧЕСКИЕ АСПЕКТЫ МУЛЬТИ ПРОФЕССОРОВ И ИХ ИСПОЛЬЗОВАНИЯ).pdf

Силовой агрегат или движок, который осуществляет перемещения на фазовом портрете это процедура автосуперпозиции, реализованная как рекуррентный генератор. Рекуррентный генератор это процедура самообращения, подающая выходной результат вновь на вход преобразователя. Именно самообращающаяся процедура выполняет роль динамического ядра процесса.

Фазовый портрет это математическая абстракция, Граф кодовых переходов не реализуется физически, например аппаратно как схемный лабиринт, по которому перемещаются самоопределяемые операнды или программно как сетевая структура данных. Фазовый портрет задаётся косвенным образом как результат взаимосвязанных трансформаций теговых кодов. Обширные фазовые портреты могут поддерживаться очень скромными аппаратными затратами. Если теговый код содержит 16 двоичных разрядов, а программа реализации оператора F состоит из менее чем десяти машинных команд, аттрактор поддерживает фазовый портрет в виде графа кодовых переходов, состоящего из сотен тысяч вершин. Уровень компрессии средств фиксации аттрактора в данном случае может составлять примерно 4 - 5 порядков. По этой причине появляется возможность не хранить детерминанты процесса в одном устройстве, осуществляющем сосредоточенное управление вычислениями, а разместить средства фиксации дискретного аттрактора непосредственно в каждом операнде и осуществить принцип распределённого управления.

Если все теговые сопровождения операндов обрабатываются одним преобразователем F, все они принадлежат одному фазовому портрету, а их теговые коды позиционируют всех и каждого на определённых вершинах графа кодовых переходов. В результате множество никак не связанных единым управлением операндов функционирует как строго согласованный ансамбль, двигающийся по заданным траекториям и реализующий заданный процесс. Уместно назвать этот эффект функциональной когерентностью.

Функциональная когерентность обеспечивается высокой степенью компрессии средств фиксации дискретного аттрактора. А компрессия возможна вследствие глубокого вырождения комбинаторики структурообразующих факторов, что означает потерю возможности задавать любые мыслимые и не мыслимые структуры фазовых портретов. В условиях компрессивного представления средств фиксации аттракторов возможные фазовые портреты образуют узкий класс структур, подчиняющихся жёстким ограничениям. Означает ли это потерю универсальности программирования любых приложений – вопрос дискуссионный. Во всяком случае следует учитывать, что не любая последовательность команд классической машины может быть осмысленной программой.

Все кодовые траектории в дискретном аттракторе сходящиеся и завершаются попаданием в цикл на графе G_F. Если цикл состоит из одной вершины, процесс останавливается. Это точка покоя дискретного аттрактора. Если цикл содержит множество вершин, аттрактор бесконечно повторяет заданную последовательность, что можно интерпретировать как постоянное циклическое выполнение определённого действия, например сканирования и контроля текущих параметров системы управления. Дискретный аттрактор обладает свойством устойчивости. Если внешнее воздействие или повреждение выбросит его из точки покоя, аттрактор сам, в соответствии с его устройством начнёт двигаться, а любые траектории движения аттрактора есть маршруты на фазовом портрете, которые всегда сходятся к точке покоя. В точке покоя механика аттрактора не выключается. Рекуррентный генератор кодовых последовательностей устроен таким образом, что в результате автосуперпозиции на выходе бесконечно порождается один и тот же код. Для внешнего наблюдателя это выглядит как останов. На самом деле дискретный аттрактор никогда не останавливается. Останов дискретного аттрактора носит условный характер, это стабильное состояние динамического равновесия, которое можно интерпретировать как непрерывный контроль равновесного состояния.

Дискретный аттрактор как динамическая система обладает определённой спецификой, которая в первую очередь заключается в том, что при формировании динамики не используется категория времени. Динамика дискретного аттрактора основана на отношениях предшествования и каждое следующее состояние порождается как функция от предыдущего. В простейшем случае, когда параллельный процесс развивается в рамках одного аттрактора по единому фазовому портрету, все события увязаны отношениями предшествования, определяемыми графом кодовых переходов. Но при усложнении ситуации, предполагающей взаимодействие процессов, размещённых на разных аттракторах, придётся решать проблему определения одновременности событий в функциональных пространствах, в которых размещены и двигаются самоопреоедяляемые данные. С этой целью придётся вводить понятия меры и измерения расстояния на фазовых портретах. При этом понадобится осуществлять переход от представления процесса как функции от предыдущего состояния к его представлению как функции от номера шага или длинны расстояния на фазовом портрете. Это одна из важнейших задач развития дискретной динамики.

Актуальной задачей дискретной динамики является конструирование фазовых портретов с заданными свойствами или, что то же, построение графов кодовых переходов с заданной топологией. Первые шаги становления дискретной динамики сделаны чисто эмпирически. С помощью простой инструментальной программы задавались рекуррентные генераторы с определённой разрядностью регистров и определённой функцией преобразования кодов и для каждого генератора строился граф кодовых переходов G_F.

Таким образом была сформирован базовая библиотека рекуррентных генераторов, представляющая базовые конструкции. Базовые конструкции известны и изображены на рис. 28. В вольной терминологии мы можем их перечислить. Это наборы самовозвратных полюсов, цепи, деревья, кольца, и розетки, представляющие собой деревья и цепи, пристыкованные к вершинам кольца. Самоовозвратными полюсами мы называем петли или минимальные циклы, состоящие из одной вершины. При этом граф может быть связен или иметь несколько компонент связности со своими циклами.

Для создания инструментальных средств дискретной динамики необходимо найти процедуру, позволяющую строить сложные конструкции фазовых портретов из простых базовых. Такая процедура существует и называется конкатенация. В наших условиях конкатенация означает совмещение двух и более регистровых секций в определённом порядке. В результате конкатенации образуется новый регистр, в котором правая секция выполняет роль младших разрядов, а левая секция роль старших разрядов объединённого регистра. Если регистры входят в состав рекуррентных генераторов и над ними построены функциональные преобразователи, в результате конкатенации образуется новый рекуррентный генератор, в котором и регистры и преобразователи образуются путём совмещения участников операции конкатенации. Иллюстрация операции конкатенации приведена на рис. 32.

Рис. 32 Конкатенация рекуррентных генераторов

Операция конкатенации объединяет два рекуррентных генератора, заданных функциями F1 и F2. Каждый из участников операции порождает свой граф кодовых переходов G_F1 и G_F2. В результате конкатенации и совмещения двух исходных рекуррентных генераторов образуется новый результирующий, который порождает новый граф кодовых переходов G_F3. Структура нового графа может существенным образом отличаться от структур участников конкатенации, а примитивная инженерная операция совмещения регистровых секций с математической точки зрения реализует нетривиальную операцию над графами. Далее приведены некоторые примеры операций над графами, возникающими при конкатенации рекуррентных генераторов.

Так, например, при конкатенации двух бинарных деревьев получается тернарное дерево. При этом глубина дерева сохраняется, а кратность ветвления умножается, рис. 33.

Рис. 33 Конкатенация двух бинарных деревьев

При конкатенации дерева и набора полюсов получается набор деревьев, т.е. связный граф превращается в многосвязный и число компонент связности равно числу полюсов в одном из участников конкатенации, рис. 34.

Рис. 34 Конкатенация дерева и набора полюсов

При конкатенации кольца и дерева, происходит образование розетки, представляющей собой набор деревьев пристыкованных к вершинам кольца, рис. 35.

Рис. 35 Конкатенация кольца и дерева

Эмпирически удалось сформировать базу данных по конкатенации разных вариантов графов кодовых переходов и выделить набор практических приёмов конструирования структур, необходимых для решения ряда практических задач. Дальнейшая разработка этого направления должна привести к обоснованию свойств операций конкатенации и построению алгебры операций над графами кодовых переходов.

До сих пор мы рассматривали варианты использования графа кодовых переходов как динамического ядра дискретного аттрактора, в котором продвижение по фазовому портрету происходит в направлении от листьев к корню дерева и циклу, которым завершается компонента связности. Для практических приложений дискретной динамики важно также обеспечить возможность продвижения по фазовому портрету в обратном направлении – от корня дерева к листьям. Эта задача не может решаться средствами функционального оператора, поскольку обратное отображение является многозначным и должно поддерживать ветвящийся процесс. Для поддержки ветвящегося процесса можно использовать гирлянду функциональных преобразователей. Гирлянда изображена на рис. 36

Рис. 36 Гирлянда функциональных преобразователей

Для примера выбрана гирлянда из трёх функциональных преобразователей, их число может меняться. Принцип действия гирлянды следует из её схемного изображения. При подаче на вход некоторого начального значения кода A₀ гирлянда откликается тремя выходными значениями А₁ , А₂ , А₃ . Далее каждое из них может подаваться на вход гирлянды и порождать на выходах следующие три значения. В данном случае рекуррентный генератор, построенный на базе гирлянды, порождает ветвящийся процесс, который носит расходящийся характер. Таким образом вводится новый базовый элемент дискретной динамики - дискретный репеллер. Дискретный репеллер это расходящийся процесс, порождаемый гирляндой функциональных преобразователей и операцией автосуперпозиции гирлянды. Фазовый портрет репеллера это расходящийся граф кодовых переходов гирлянды. Репеллер по определению не имеет остановки и порождает бесконечный расходящийся процесс. Вследствие конечности набора кодов, на котором определены функциональные преобразователи гирлянды рано или поздно запас кодов исчерпывается и на выходе гирлянды появляется код, который ранее уже имел вхождение в вершины графа кодовых переходов. Это означает, что фрагмент дерева, начинающийся с данной вершины будет воспроизведен репеллером вновь. В целом фазовый портрет репеллера будет состоять из бесконечного повторения конечного набора фрагментов, графа кодовых переходов, заданного гирляндой. Исследование динамики развития процессов в репеллерах это следующий и очень содержательный раздел дискретной динамики.

Опираясь на понятия дискретный аттрактор и дискретный репеллер можно сформулировать важное для приложений дискретной динамики понятие реверсивный аттрактор. Допустим, что задан дискретный аттрактор с определенным фазовым портретом. Для построения реверсивного аттрактора необходимо синтезировать репеллер, фазовый портрет которого совпадает с фазовым портретом аттрактора с точностью до инверсии направления рёбер графа кодовых переходов. Реверсивный аттрактор это сопряжённая пара аттрактора и репеллера, обеспечивающая продвижение процесса по заданному фазовому портрету в прямом и обратном направлениях. Задача эта решается следующим образом. Исходный аттрактор задаётся рекуррентным генератором на базе определённой целочисленной функции. График функции представляется как совокупность точек на целочисленной квадратной решётке. График изображён на рис. 37а.

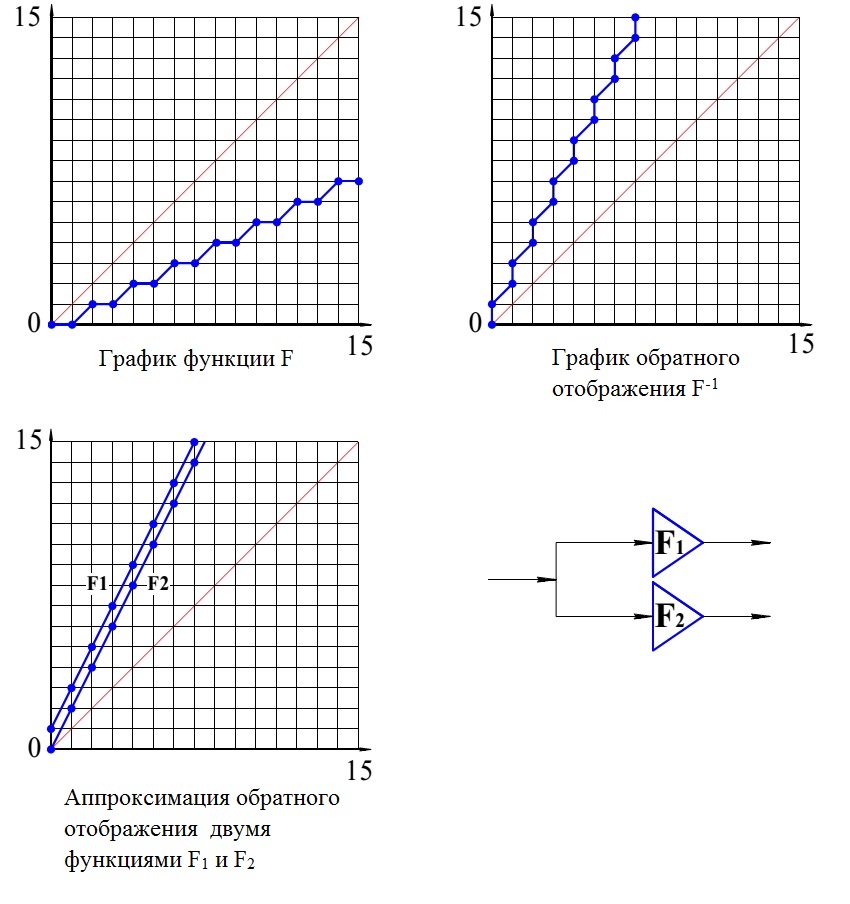
Рис. 37 Процедура построения реверсивного аттрактора

По данному графику необходимо построить обратное отображение. Для этого надо выполнить операцию замены координат, что достигается поворотом исходного графика вокруг главной диагонали. График обратного отображения изображён на рис. 37б. Обратное отображение не является функциональным и далее надо решить задачу синтеза набора сопряжённых функций, покрывающих, полученный график обратного отображения. Перечисленные действия изображены на рис. 37

Эта задача не имеет общего решения. В каждом конкретном случае путём подбора можно найти множество вариантов покрытия графика обратного отображения функциональными графиками и искать среди них приемлемые по критерию удобства реализации сопряжённых функций. Из полученного таким образом набора сопряжённых функций составляется гирлянда для реализации репеллера, дополнительного к заданному аттрактору.

Рассмотренные до сих пор средства формирования графов кодовых переходов предполагают, что каждое регистровое состояние из множества, образующего структуру имеет однократное вхождение в граф кодовых переходов. В практике применения дискретных аттракторов для формирования вычислительных работ необходимо обеспечить многократную повторяемость кодов операций на графе вычислительного процесса. Это достигается путём наложения маски на образующие регистры и чтения из под маски только части разрядов, необходимых для кодирования операций. Рассмотрим конкретный пример. Необходимо построить граф кодовых переходов со структурой сильно ветвящегося дерева с кратностью ветвления равной 8 и заданной глубиной 4 уровня. При этом ставится задача обеспечить возможность полной нумерации предшественников каждой вершины. Выберем определённую вершину и рассмотрим набор из восьми вершин, являющихся предшественниками данной. Коды вершин предшественников должны быть устроены таким образом, чтобы при наложении на них определённой маски можно было извлечь три разряда, задающих полную нумерацию предшественников от 0 до 7, или в двоичном выражении от комбинации 000 до 111. По принятому условию это свойство должно выполняться для всех вершин кроме листовых, которые не имеют предшественников.