Файл: Мультипроцессоры (ТЕОРЕТИЧЕСКИЕ АСПЕКТЫ МУЛЬТИ ПРОФЕССОРОВ И ИХ ИСПОЛЬЗОВАНИЯ).pdf

Приведем на обозрение единственный известный нам проект в соответствии с программой Бэкуса в конце 80-х годов. Проект назывался редукционно-потоковая машина, основные сведения по проекту содержатся в патенте [17]. Программа разработки моделей и постановки модельных экспериментов была успешно выполнена. Структура моделей и основные результаты моделирования изложены в [18]. Представим на рис. 2 кривые роста коэффициента ускорения , который представляет собой отношение времени выполнения задачи на одном процессоре к времени выполнения задачи в многопроцессорной системе. При этом временные затраты оценивались в числе квантов модельного времени.

Рис. 2 Зависимость коэффициента ускорения от числа каналов обработки при разных значениях средней трудоёмкости пакетов

Главным выводом этого эксперимента явилось то, что реальные значения коэффициента ускорения оказываются неприемлемо низкими, а график роста входит в насыщение при относительно малом значении параллелизма – при 6 каналах обработки. Модель была построена для 16 каналов и в этом диапазоне показателя параллелизма коэффициент ускорения вышел на уровень 2,8 и далее не менялся. Полученные результаты моделирования означали приговор всему проекту. Поставленная цель – освоение массового динамического параллелизма средствами данного проекта не могла быть достигнута.

1.2 Результаты измерений производительности при выполнении алгоритмов БПФ

Проблема быстрой остановки роста производительности при наращивании степени параллелизма никуда не делась и со временем проявилась на макроуровне при эксплуатации кластеров и суперкомпьютеров. В этой связи целесообразно рассмотреть данные, полученные пользователями многопроцессорных систем в ходе исследования эффективности параллельного выполнения алгоритмов трёхмерного быстрого преобразования Фурье (3D БПФ), изложенные в [19]. Отметим, что существуют многочисленные версии специальных многопроцессорных систем, ориентированных на параллельное выполнение алгоритмов БПФ. Эти специализированные системы эффективно выполняют только один алгоритм – БПФ, другими алгоритмами их, как правило, не загружают. В тоже время алгоритмы БПФ являются наиболее проблемными при загрузке в универсальные параллельные системы. Именно алгоритмы БПФ характеризуются большими объёмами перекрёстных пересылок данных, в переходах, связывающих параллельные слои в общем графе алгоритма.

Приведём данные измерений временных затрат и вычисленные показатели ускорения в виде графиков из [19] и прокомментируем их.

Рис. 3 Ускорения, полученные при прогоне алгоритмов 3D БПФ на установке Beowulf Cluster

Рис. 4 Временные затраты при прогоне алгоритмов 3D БПФ

на установке Beowulf Cluster

Временные затраты получены в результате измерений, ускорения вычислены. В прогоне участвовали два варианта решения задачи - с размерностью 64х64х64 и с размерностью 128х128х128. Установка Beowulf Cluster это примитивный кластер, созданный на базе набора персональных компьютеров, объединённых средствами локальной офисной сети.

Вторая серия экспериментов выполнялась на установке Beowulf Cluster с более мощным коммутатором и более скоростной шиной. Результаты проведены на рис. 5 и рис. 6.

Рис.5 Ускорения, полученные при прогоне алгоритмов 3D БПФ

на улучшенной установке Beowulf Cluster

Рис. 6 Временные затраты при прогоне алгоритмов 3D БПФ

на улучшенной установке Beowulf Cluster

И наконец, авторы [19] получили доступ к более совершенной установке IBM SP2, построенной на базе скоростного коммутатора с развитой системой шин. Данные экспериментов приведены на рис.7 и рис 8.

Рис. 7 Ускорения, полученные при прогоне алгоритмов 3D БПФ

на установке IBM SP2

Рис. 8 Временные затраты при прогоне алгоритмов 3D БПФ

на установке IBM SP2

Приведенная последовательность графиков показывает, что при прогоне алгоритмов с высоким потенциалом параллелизма коэффициенты ускорения довольно низкие и после прохождения пика резко падают. Ситуация заметно улучшается по мере улучшения обменной среды, поддерживающей межпроцессорные передачи.

Схожие результаты на рис. 9 получили авторы статьи [20] в рамках реализации алгоритма Radix-4 БПФ на суперкомпьютере К-100 ИПМ РАН.

Рис. 9 Графики ускорений, полученных при вычислении алгоритма БПФ с различной длиной входного массива на кластере К-100

Как видно из графиков, максимальное ускорение не достигало 5, а на большом числе узлов, как и в работе [19], наблюдается спад.

1.3 Анализ факторов, ограничивающих рост производительности параллельных систем

Подведём итог. Рассмотрены ситуации роста производительности в двух достаточно разных средах – в классической многопроцессорной системе с общей шиной и в перспективном проекте неклассической архитектуры с элементами Data Flow. При этом результаты экспериментов похожие, если не сказать подобные. В случае с редукционно-потоковой машиной рассматривался результат модельного эксперимента, в случае с классической структурой получены данные измерений натурного эксперимента. В обоих случаях ход графиков роста коэффициента ускорения очень похож на графики, иллюстрирующие проявления закона Амдала. Однако надо сразу отметить, что наблюдаемый нами эффект быстрого прекращения роста производительности к закону Амдала не имеет никакого отношения, поскольку в обоих случаях насыщение наступает задолго до исчерпания потенциала параллелизма задачи. Мы имеем дело с другим явлением, природу и физический смысл которого предстоит выяснить.

Построим модель распределения временных затрат при параллельных вычислениях на конкретном примере реализации алгоритма быстрого преобразования Фурье (БПФ). На рис. 10 приведен граф процесса вычисления алгоритма 16-точечного БПФ. В данном случае размерность БПФ выбрана по соображениям наглядности и удобства визуального восприятия рисунка. Нам необходимо проиллюстрировать топологическую природу графа, представляющего регулярную сетку с определённым принципом построения. Далее известно, что граф процесса вычисления алгоритма БПФ легко масштабируется на любую размерность по степеням двойки.

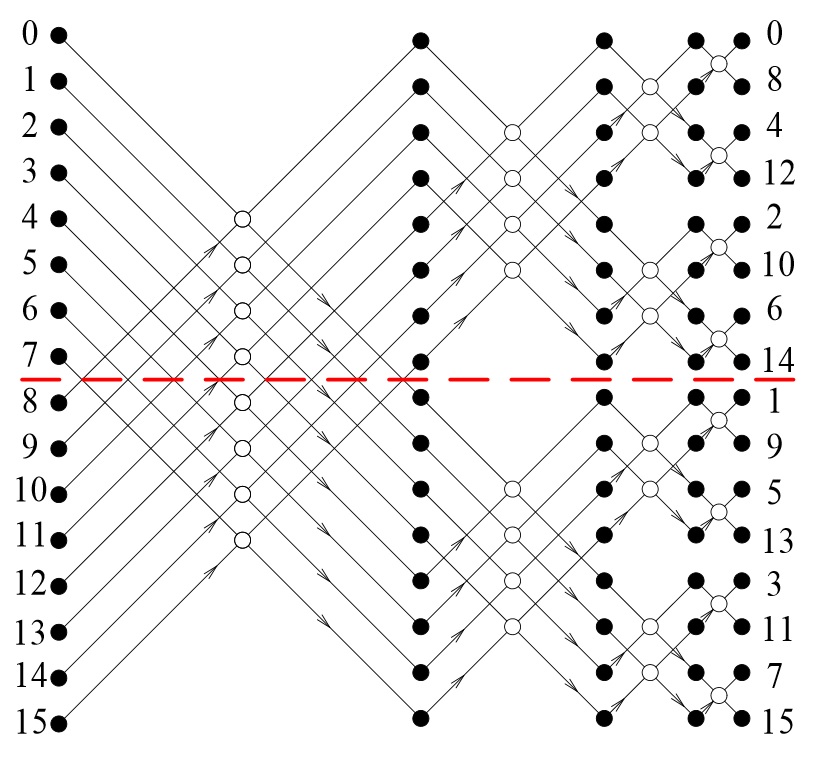
Рис. 10 Граф процесса вычисления 16-точечного БПФ

Сплошными кружочками на рисунке обозначены комплексные операнды, записанные в алгебраической форме, каждый из которых представляются парой действительных коэффициентов. Нумерация операндов в левой части рисунка отображает порядок следования отсчётов во входной сигнальной последовательности. На выходе происходит перестановка порядка следования отсчётов, это побочный эффект данного алгоритма. Контурные кружочки обозначают базовую процедуру с двумя входами и двумя выходами, называемую бабочкой БПФ. Базовая процедура представляет собой алгоритм решения системы четырёх алгебраических уравнений. На выходе базовой процедуры порождается пара комплексных чисел, каждое из которых представлено парой действительных коэффициентов. Намеренно опустим целый ряд деталей с целью установления основных свойств графа вычисления БПФ; для нас важно, что граф носит регулярный характер. На рис. 10 видно, что структура графа разбивается на ряд вертикальных слоёв, представленных одним числом вычислительных процедур. Вся структура графа заполнена одной базовой вычислительной процедурой, которая принимает на входе и порождает на выходе одни и те же форматы данных. Параллелизм обработки данных осуществляется в пределах слоя, слои образуют последовательность, при переходах между слоями осуществляется обмен данными. Фазы параллельной обработки и фазы обменов данными идентичны по всему графу, что позволяет корректно провести подсчёт временных затрат на осуществление вычислительных и обменных операций.

Размерность алгоритма наращивается по степеням двойки и если число входных отсчётов равно , то число слоёв в графе равно , а число вычислительных процедур в слое равно . Соответственно общее число процедур в графе равно . Основные показатели структуры графа, необходимые для вычисления производительности параллельного представления процесса масштабируются, что позволяет нам воспользоваться наглядностью графического представления 16-точечного БПФ и далее пересчитать требуемые характеристики для любой другой размерности. Для 16-точечного БПФ имеем следующие показатели число слоёв в графе равно 4, число базовых процедур в слое равно 8, всего процедур в графе 32. Задача состоит в том, что бы построить модель вычисления коэффициента ускорения, в которой в явном виде учитываются время вычисления базовых процедур и время передачи данных между процессорами при переходах с текущего слоя на следующий. При этом мы определяем время обмена данными как сумму времени передачи данных и времени выполнения протокольных событий, обеспечивающих доступ к обменной среде.

Определим ускорение как отношение времени выполнения алгоритма на одном процессоре ко времени выполнения алгоритма на процессорах , где размерность алгоритма, а - число процессоров. Поскольку искомое ускорение есть величина относительная для данной модели мы будем оценивать времена выполнения определённых действий в условных микротактах работы оборудования. Примем, что время выполнения базовой операции равно 10 микротактам. Тогда время выполнения 16-точечного БПФ на одном процессоре будет состоять только из времени выполнения базовых операций, поскольку обмен данными при этом отсутствует.

Числитель будет состоять из трёх членов, зависящих от числа процессоров n . Время вычисления базовых процедур будет равно . Или в общем виде

Для определения времени пересылки данных необходимо рассмотреть структуру графа на рис. 10. При двух процессорах граф будет рассечен на две части по горизонтальному направлению как это отмечено пунктирной линией и две его половины будут загружены в разные процессоры. В этом случае обмен данными произойдёт только при переходе с первого на второй слой. При этом в каждом из двух процессоров будет вычисляться по 4 бабочки и каждая из них будет располагать только половиной входных данных, а вторую половину данных необходимо будет получить из другого процессора. Следовательно, обмен будет состоять из двух сеансов передач, содержащих по 4 отсчёта. Общий объём пересылаемых данных составит отсчётов.

При 4-х процессорах верхняя и нижняя половинки графа рассекаются аналогичным образом. В этом случае появляется необходимость обмена данными при переходе со второго на третий слой, объём пересылаемых данных по прежнему равен отсчётов, а суммарный объём составит . Для 8 процессоров каждая выделенная по горизонтали часть графа вновь рассекается на две и мы получаем параллельное представление всего графа, состоящее из восьми последовательных нитей, каждая из которых содержит последовательность из трёх базовых операций. При этом появляется необходимость обменов при переходе со второго на третий слой с тем же объёмом передаваемых данных. Общий объём обменов будет равен . отсчётов. Таким образом, в общем случае число передаваемых отсчётов будет равно .

Протокольные события в обменной среде сопровождают сеансы связи и в упрощённой ситуации их подсчёт можно осуществить как некоторое фиксированное время, выраженное в условных микротактах и привязанное к сеансу связи. По мере наращивания числа процессоров происходит увеличение числа сеансов и уменьшение объёмов данных, передаваемых в каждом сеансе. При двух процессорах происходит один обмен па переходе от первого слоя ко второму, который состоит из 2 сеансов – от первого процессора ко второму и от второго к первому. При четырёх процессорах имеет место 2 обмена, в каждом из которых осуществляется по 4 сеанса и общее число сеансов равно 4 + 4. При восьми процессорах происходит три обмена и в каждом из них по 8 сеансов, всего 8 + 8 + 8. Таким образом, в общем случае число сеансов может быть определено как .

Посчитаем общие затраты времени при 2 процессорах. Время вычисления сократится вдвое и составит условных микротактов.

Время передачи данных учитывается как объём передаваемых данных приведенный к пропускной способности шины. При двух процессорах осуществляется передача восьми отсчётов по два слова в каждом, что равно 16 словам. По определению мы принимаем производительность шины равную передаче 1 слова за один микротакт, следовательно, искомое время обмена данными составит 16 условных микротактов.

Временные затраты на осуществление протокольных событий вычисляется как затраты на один протокол умноженные на число сеансов. Примем по определению, что на один протокол затрачивается 5 условных микротактов. Для данного случая, осуществления одного обмена, состоящего из двух сеансов, это составит .

Таким образом, суммарные временные затраты на вычисление 16-точечного БПФ В нашей модели при двух процессорных элементах составляют 186 условных микротактов, а коэффициент ускорения = 1,72. Аналогично проводится подсчёт для 4 и 8 процессоров. Данные сведены в Таблицу 1.