Файл: Мультипроцессоры (ТЕОРЕТИЧЕСКИЕ АСПЕКТЫ МУЛЬТИ ПРОФЕССОРОВ И ИХ ИСПОЛЬЗОВАНИЯ).pdf
Добавлен: 27.06.2023
Просмотров: 153
Скачиваний: 3
СОДЕРЖАНИЕ
ГЛАВА 1 ТЕОРЕТИЧЕСКИЕ АСПЕКТЫ МУЛЬТИ ПРОФЕССОРОВ И ИХ ИСПОЛЬЗОВАНИЯ
1.1 Некоторые этапы из истории освоения массового параллелизма
1.2 Результаты измерений производительности при выполнении алгоритмов БПФ
1.3 Анализ факторов, ограничивающих рост производительности параллельных систем
ГЛАВА 2 ПРАКТИЧЕСКИЕ АСПЕКТЫ ПРИМЕНЕНИЯ МУЛЬТИПРОЦЕССОРОВ
2.1 Обзор работ по коммутационным средам
2.2 Оценка эффективности реализации вычислений
2.3 Архитектура самоопределяемых данных и принципы распределенного управления
2.3 Краткое описание математического аппарата дискретной динамики
Искомый рекуррентный генератор, поддерживающий заданное сильно ветвящееся дерево будет сформирован в результате конкатенации трёх генераторов, поддерживающих четырёхэтажные бинарные деревья и построенные на базе уже известной нам функции сдвига вправо на один разряд. По известным нам свойствам операции конкатенации бинарных деревьев глубина сохраняется равной 4, а кратности ветвления перемножаются и дают требуемое значение 8. В итоге получается полное четырёхэтажное дерево с кратностью ветвления равной 8. А теперь наложим на образующие регистры маску, которая позволяет извлечь из каждой секции участвующей в конкатенации один младший крайний правый разряд. Трехразрядный код, извлечённый в результате маскирования, содержит полную нумерацию вершин предшественников. Остальные разряды полного кода позиционируют вершины на дереве в целом. На рис. 38 приведен фрагмент сильно ветвящегося дерева с реальными значениями кодов вершин и показано извлечение полной нумерации вершин предшественников.
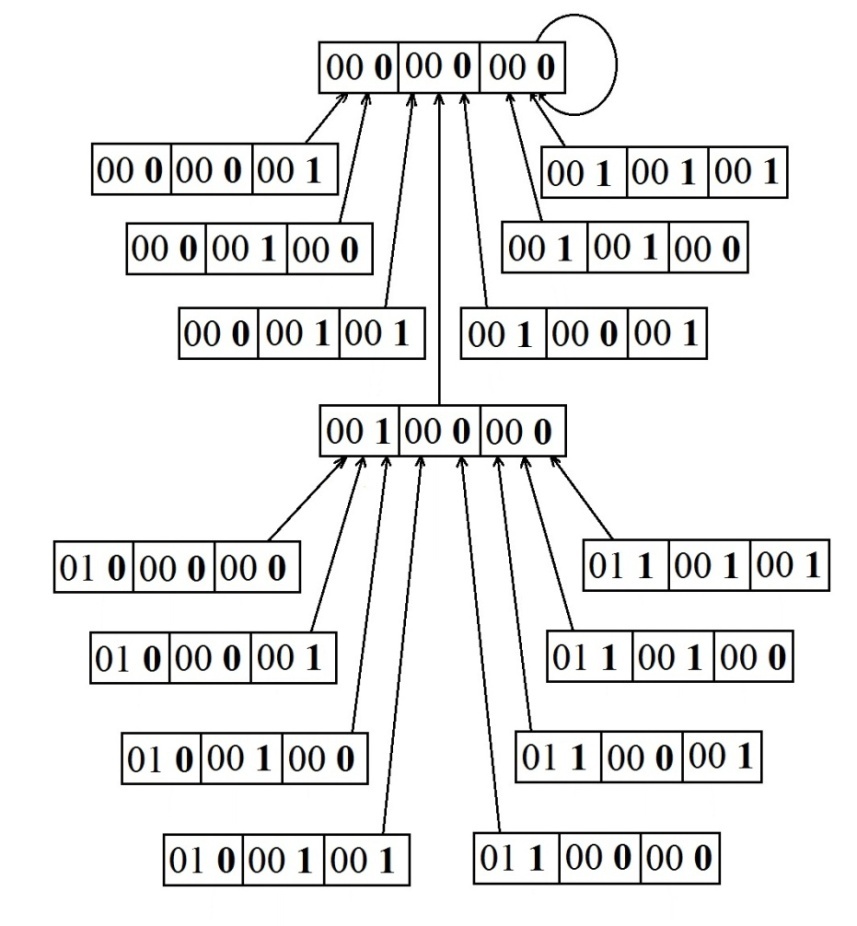
Рис. 38 Извлечение из-под маски полной нумерации вершин предшественников
Разряды кодов, извлекаемые маской обозначены жирным шрифтом и отделены пробелом.
Весь объём изложенных выше понятий и механизмов дискретной динамики необходим для обсуждения возможной технологии программирования вычислений в архитектуре самоопределяемых данных. Задача ставится следующим образом: задано арифметическое выражение, по которому строится граф вычисления в виде бинарного дерева и затем синтезируется дискретный аттрактор, фазовый портрет которого накрывает этот граф. Для решения поставленной задачи построим дискретный аттрактор с фазовым портретом в виде сильно ветвящегося дерева, в котором содержатся бинарные поддеревья вычисления всех возможных арифметических выражений, не превышающих определённый уровень сложности, ограниченный глубиной дерева вычисления. Работа аттрактора запускается загрузкой в вычислитель набора исходных операндов. Теговые коды исходных операндов позиционируют начальное состояние процесса на фазовом портрете. Дальнейшие события разворачиваются детерминировано и определяются конструкцией аттрактора и структурой фазового портрета. Правильно загруженный набор исходных операндов извлекает из фазового портрета своё бинарное поддерево. Следовательно, для программирования заданного вычисления необходимо отыскать, соответствующие ему листовые вершины и присвоить их коды исходным операндам в виде теговых сопровождений.
Для отыскания листовых вершин заданного вычисления необходимо наложить заданное бинарное дерево на общее сильно ветвящееся. Предполагается, что нумерация вершин предшественников увязана в таблицу кодирования арифметических операций. Размещение начинается с корневой вершины. Выбирается заключительная операция заданного вычисления и ставится маркер на вершину предшественницу корня, номер которой соответствует заключительной операции. Два операнда, участвующие в заключительной операции порождаются выполнением двух предшествующих арифметических операций, что обнаруживается при раскрытии скобок в направлении от главной заключительной операции. На следующем шаге необходимо поставить маркерные метки на двух вершинах, предшествующих отмаркированной на первом шаге. При этом следует отбирать вершины с номером, соответствующим кодам предшествующих арифметических операций. Если бы предшествующие операции всегда были разными, можно было бы ограничиться ветвлением общего дерева с кратностью равной четырём. Но в общем случае обе предшествующие операции могут быть одинаковыми. По этой причине в номерах предшествующих вершин каждая операция должна быть представлена дважды. Вот почему при четырёх операциях понадобилось дерево с кратностью ветвления равной восьми. Описанная процедура повторяется до исчерпания операций в исходной записи арифметического выражения. Последние маркерные метки отмечают листовые вершины бинарного дерева искомого вычислительного процесса. Результат программирования в данном случае это назначение теговых кодов исходным операндам. При загрузке в вычислитель исходные операнды запускают вычислительный процесс и извлекают требуемое бинарное поддерево путём прохождения своих маршрутов на фазовом портрете.
Разработанные ранее инструментальные средства дискретной динамики позволяют сконструировать компилятор, осуществляющий программирование процессов вычисления арифметических выражений в архитектуре самоопределяемых данных. Для этого есть инструменты формирования сильно ветвящихся деревьев, есть инструменты маскирования кодов для организации полной нумерации вершин предшественников, есть методы построения реверсивных аттракторов, обеспечивающих движение по фазовому портрету в прямом и обратном направлениях. Описанный компилятор можно сделать полностью автоматическим.
Поддержка полного сильно ветвящегося дерева необходима для работы компилятора, который должен содержать пути для вычисления всех возможных арифметических выражений. После выбора заданного выражения и завершения компиляции поддержка полных теговых кодов при исполнении процесса становится избыточной. Возможна оптимизация, которая означает сокращение разрядности тегов. Сокращение разрядности теговых кодов должно происходить при условии, что общая конструкция графа кодовых переходов не нарушается, выбранное бинарное поддерево сохраняется, а лишние ветви полного сильно ветвящегося дерева отсекаются. Такая задача может быть поставлена и есть предположения по её решению. Задача не имеет общего решения, это означает, что в каждом конкретном случае эффективность сокращения разрядности теговых сопровождений будет различной.
Приведем пример. Рассмотрим наложение функции на граф результата конкатенации трех функций побитового сдвига разрядности 4. Вышеописанным способом наложим на этот граф маску, предварительно поделив двоичное представление значений в его вершинах уже не на тройки, а на четверки. Составим таблицу соответствия кодов, не попавших под маску. Таким образом, применив эту таблицу к графу получим граф - фазовый портрет, где в вершинах уже стоят простейшие операции сложения, вычитания, умножения и деления. Теперь же построим граф нашей функции, где в листовых вершинах будут стоят операнды, а во всех остальных все те же простейшие операции. Целью задачи является поиск маршрута вычисления малого графа на большом, путем наложения одного на другой. Начиная с корневых вершин попарно сравним значения вершин в графах и подберем соответствующие по совпадению указанных в них операций . Результат наложения приведен на рис. 39. Отметим, что приведен не граф целиком, а лишь совпавший фрагмент. Проиллюстрировать наложение полностью не представляется возможным в силу большого размера графа.
Рис. 39 Фрагмент наложения искомого графа на граф конкатенации.
ЗАКЛЮЧЕНИЕ
Оценка современного состояния технологии микроэлектронного производства позволяет сделать вывод о том, что в ближайшее десятилетие рост тактовой частоты прекратится и будет зафиксировано оптимальной значение 2.2 ГГц. При этом рост числа транзисторов продолжится и достигнет значений порядка десятка миллиардов на одном кристалле. Это означает, что закон Мура переформатируется в требование удвоения числа процессорных ядер с периодом 18 – 24 месяцев. Следовательно, основой роста производительности вычислительных средств в ближайшей перспективе становится освоение массового параллелизма. В работе показано, что рост производительности вычислительных средств в широком диапазоне значений параллелизма в общем случае не возможен. Обзор публикаций по опыту эксплуатации высокопараллельных систем показывает наличие эффекта быстрого насыщения роста производительности при значениях ускорения в 6-8 раз при 10-16 процессорных элементах для задач имеющих потенциал параллелизма в сотни и тысячи независимых событий. В работе были проанализированы и вскрыты причины подавления роста производительности, связанные с обменными операциями пересылки данных между параллельными ветвями процессов. Баланс временных затрат таков, что время счёта быстро падает и его вклад в общие затраты становится относительно ничтожным, но при этом агрессивно и устойчиво растут затраты на обмен данными. Сделан обзор современных и перспективных разработок по развитию обменной коммутационной среды. Показано, что ожидаемый рост производительности коммутационных сред не в состоянии переломить тенденции роста затрат на обслуживание параллелизма и способен только незначительно переместить точку насыщения роста производительности. Предпринят анализ эффективности организации вычислений в классической архитектуре, выведены экспертные оценки, показывающие, что КПД современного компьютера не превышает одного процента. Другими словами на одно полезное действие приходится не менее ста обеспечивающих затратных. Строить высокопараллельные системы при такой эффективности организации процессов бесперспективно, поскольку издержки растут кратно параллелизму, а быстро растущие специфические затраты на обслуживание параллелизма приводят опережающему росту суммарных издержек и делают массовый параллелизм бессмысленным. В работе проанализированы источники издержек и показано, что порождающей причиной являются фундаментальные принципы организации вычислений, основанные на идее централизованного управления разделении потоков команд и потоков данных. Данные хранятся в специальной среде хранения (памяти), а обрабатываются в среде обработки (процессорах). Для осуществления обработки необходимо осуществлять массовые пересылки данных из мест хранения к местам обработки и обратно. При массовом параллелизме эта проблема быстро обостряется и демонстрирует принципиальную несостоятельность архитектурной идеи. В качестве альтернативы предложена архитектура самоопределяемых данных, в которой реализован принцип слияния данных и командной информации в единый формат самоопределяемых операндов. Самоопределяемые операнды строятся аналогично пакетам в сетях пакетной коммутации и состоят из информационных полей, сопровождаемых набором командных полей, управляющих перемещением операндов, селекцией партнёров для обработки и выбором функций обработки. При этом реализуется принцип распределённого управления и устраняются паразитные пересылки – самоопределяемые данные обрабатываются там же где хранятся - в совмещённой функциональной среде. Таким образом создаётся перспектива эффективной реализации массового динамического параллелизма. При этом реализуется принцип распределённого управления, а это ставит проблему программирования самоопределяемых данных. Сделан выбор математического аппарата и излагаются основы дискретной динамики, Вводятся базовые понятия - дискретный аттрактор, фазовый портрет, реверсивный аттрактор и ряд других. Дискретная динамика описывает среду, в которой существуют, двигаются и обрабатываются самоопределяемые данные. В терминах дискретной динамики ставится и решается задача программирования самоопределяемых данных как задача синтеза фазовых портретов с заданной топологией. Описываются принципы построения компилятора, работа которого иллюстрируется на конкретном примере.
СПИСОК ЛИТЕРАТУРЫ
[1] Шайтан К.В., Антонов М.Ю., Шайтан А.К., Новоселецкий В.Н., Боздагонян М.Е., Касимова М.А. Метод молекулярной динамики в исследованиях свойств биологических объектов // Наноструктуры. Математическая физика и моделирование., 2012, 6 (1,2), 63-79.
[2] Блинов В.Н., Совенюк А.А. Программирование задач физики конденсированного состояния с использованием MPI // Наноструктуры. Математическая физика и моделирование., 2012, 7 (1), 5-107.
[3] Викул Е.А., Тужилин А.А. Геометрия аминокислот и полипептидов: случай рентгеноструктурного анализа // Наноструктуры. Математическая физика и моделирование., 2014, 11 (2), 5-29.
[4] Григоренко Б.Л., Князева М.А., Исаев Д.А., Новичкова А.В., Немухин А.В. Компьютерное моделирование химических реакций в сложных биологических системах // Наноструктуры. Математическая физика и моделирование., 2014, 10 (2), 95-107.
[5] Блинов В.Н. Дальнодействующие взаимодействия в компьютерном моделировании систем в конденсированном состоянии // Наноструктуры. Математическая физика и моделирование., 2014, 10 (1) 5-29.
[6] Ожигов Ю.И. Представление декогерентности при компьютерном моделировании квантовых состояний наносистем // Наноструктуры. Математическая физика и моделирование., 2013 8 (1) 47-65.
[7] Обзор продуктов семейства Tesla Kepler // NVIDIA.RU: NVIDIA Tesla GPU Accelerators, сайт производителя. URL:
http://www.nvidia.ru/content/tesla/pdf/NVIDIA-Tesla-Kepler-
[8] Черняк Л. Многоядерные процессоры и грядущая параллельная революция.// Открытые системы 2007 4 , 33-42.
[9] Воеводин В.В. Математические основы параллельных вычислений // ННГУ 2009 .583 стр.
[10] Sidlausakas D. Lecture on multicores // Danish National Research Foundation, Madalgo, 12.03.2013, p. 8. URL:
http://www.cs.au.dk/~gerth/ae13/slides/multicores.pdf
[11] Gene M. Amdahl. Validity of the single processor approach to achieving large scale computing capabilities // IBM Sunny vale, California. AFIPS spring joint computer conference. 1967. URL:
http://www-inst.eecs.berkeley.edu/~n252/paper/Amdahl.pdf
[12] Dennis J. B. First version of Data Flow procedure language // Lecture Notes in Computer Science 1974, 363 - 376.
[13] Городня Л.Г. Основы функционального программирования // М., 2004 280 с.
[14] Амамия М., Танака Ю. Архитектура ЭВМ и искусственный интеллект // Мир, Москва, 1993 397 с.
[15] Галушкин А.И., Точенов В.А. Транспьютерные системы – начало становления в России ЭВМ с массовым параллелизмом // Нейрокомпьютер, , 2005 3, 22-38.
[16] Backus J. Can Programming Be Liberated from von Neumann Style? A Functional Style and Its Algebra of programs // 1977 Turing Award Lecture, P. 63-130.
http://rkka21.ru/docs/turing-award/jb1977r.pdf
http://rkka21.ru/docs/turing-award/jb1977e.pdf
[17] Махиборода А.В. и другие, Система потоковой обработки информации с интерпретацией функциональных языков // Авторское свидетельство № 1697084 опубликовано 29. 06. 1989 г. Положительное решение 25.05 1990 г.
[18] Соколовский Ю.Л. Предпроектное исследование персональной ЭВМ редукционно-потокового типа средствами имитационного моделирования // Препринт 92-17, Институт кибернетики АН УССР, Киев 1992 30 стр.
[19] Cramer C. Board J. The Development and Integration of Distributer 3D FFT for a Cluster of Workstations // «4th Annual Linux Showcase & Conference, Atlanta October 10-14 2000», Pp. 121–128 of the Proceeding.
[20] Морозов А.А., Тимофеев А.В. Эффективность параллельной реализации алгоритма Radix-4 быстрого преобразования Фурье // Наноструктуры. Математическая физика и моделирование., 2016 14 (1) 69-82.
[21] Duato J.,Yalamanchili S., Ni L. Interconnection Networks An Engineering Approach // MORGAN KAUFMANN PUBLISHERS, 2003.
[22] Borkar S., et al., iWarp: An integrated solution to high-speed parallel computing // Proceedings of Supercomputing'88, November 1988, 330-339.
[23] Kim J., Dally W.J., Scott S., Abts D. Technology-Driven, Highly-Scalable Dragonfly Topology // Northwestern University, Stanford University.
[24] Норман Г.Э., Орехов Н.Д., Писарев В.В., Смирнов Г.С., Стариков С.В., Стегайлов В.В., Янилкин А.В. Зачем и какие суперкомпьютеры экзафлопсного класса нужны в естественных науках // ПРОГРАММНЫЕ СИСТЕМЫ: ТЕОРИЯ И ПРИЛОЖЕНИЯ №4(27), 2015, 243–311.
[25] Yadav S., Mishra R., Gupta U. Performance Evaluation of Different Versions of 2D Torus Network // Computer Science and Engineering. 2015 International Conference on Advances in Computer Engineering and Applications.
[26] Dally W.J., Poulton J.W. Digital systems engineering // Cambridge University Press, New York, NY, 1998.
[27] Resources for Embedded and IoT Designers. URL: http://www.intel.com/design/network/products/optical/cables/index.htm
[28] Kim J., Dally W.J., Abts D. Flattened Butterfly : A Cost-Efficient Topology for High-Radix Networks // In Proc. of the International Symposium on Computer Architecture (ISCA), San Diego, CA, June 2007, 126–137.
[29] Leiserson C. Fat-trees: Universal networks for hardware efficient supercomputing // IEEE Transactions on Computer, C-34(10):892–901, October 1985.
[30] Дурнев В.Г., Стандрик В.Д. // Основы построения систем передачи ЕАСС, Радиоисвязь 1985, 208 с.
[31] Мизин И.А., Богатырёв В.А., Кулешов А.П. Сети коммутации пакетов // Радио и связь. М. 1986 г 408 с.
[32] Мизин И.А., Махиборода А.В. Концепция самоопределяемых данных и архитектура распределённых систем // Информационные технологии и вычислительные системы, Москва, Наука, №1 , 1995 г., 21 - 31.