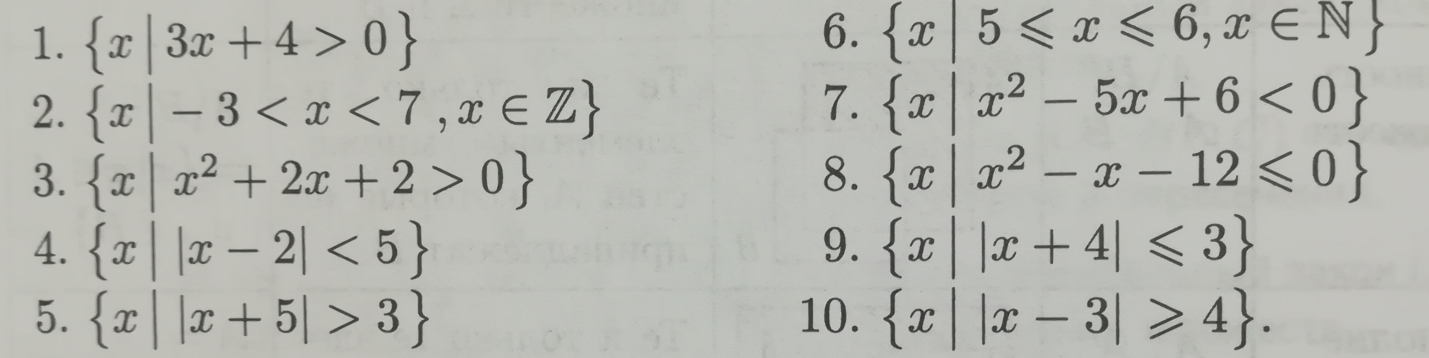ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.08.2020
Просмотров: 245
Скачиваний: 7
Раздел 1. Основы теории множеств
Тема 1.1 Основные понятия теории множеств
Содержание темы: основные принципы теории множеств; понятие множества; конечные и бесконечные множества, пустое множество; подмножество, количество подмножеств конечного множества; теоретико множественные диаграммы.
Понятие множества является основополагающим понятием классической математики. Создателем теории множеств является немецкий математик Георг Кантор.
Можно дать следующее описательное определение множества: Множество – это совокупность каких-либо объектов, объединенных общим признаком или свойством.
Объекты, которые образуют множество, называются элементами этого множества.
Примеры: множество всех страниц книги, множество всех натуральных чисел N.
Множества обозначаются большими латинскими буквами A, B, C,…,X,Y,…, а их элементы – a, b, c,…,x,y,…
Если
элемент a
является элементом множества A,
то пишут
(а принадлежит А). Если элемента a
не является элементом множества A,
то пишут
(а не принадлежит А).
Если элементы множества являются числами, то множество называется числовым. Многие из числовых множеств имеют специальные названия и обозначения.
Множество
действительных чисел x,
удовлетворяющих неравенствам
(
)
называется отрезком
(интервалом)
и обозначается [a;b]
((a;b)).
Полуинтервалом
[a;b)
((a;b])
называется множество действительных
чисел x,
удовлетворяющих неравенствам
(
).
Множества
действительных чисел x,
удовлетворяющих условию
(
)
или
(
)
обозначаются соответственно
(
)
или
(
).
Если множество содержит лишь конечное число элементов, то оно называется конечным. В противном случае множество называется бесконечным.
Примеры: множество людей на Земле – конечное множество; множество целых чисел – бесконечное множество.
Множество, не содержащее ни одного элемента, называется пустым и обозначается Ø.
Существуют различные способы задания множества. Наиболее простой заключается в указании всех элементов множества.
Пример:
Если множество элементов бесконечно, то используется многоточие.
Пример:
множество натуральных чисел
Другой
способ задания множества состоит в
описании элементов характеристическим
(определяющим) свойством P(x),
общим для всех элементов A:
.
Примеры:
- множество четных натуральных чисел;
-
множество, состоящее из 2, 4, 6, 8;
-
множество, состоящее из пациентов
определенной больницы.
Если множества А и В состоят из одних и тех же элементов, то есть если каждый элемент множества А является элементом множества В и наоборот, то множества А и В равны. Обозначение: А=В.
Пример:
.
Пусть
имеются два множества А и В. Если каждый
элемент множества В является элементом
множества А, то В является подмножеством
множества А. Обозначение:
(В включено в А).
Примеры:
;
А={x:
вид животных}, В={x:
вид млекопитающих}. Тогда
.
Множество всех подмножеств множества X называется булеаном или степенью множества. Обозначение: B(X).
Если множество А имеет n элементов, то булеан множества А содержит 2n элементов, то есть Р(А)=2n, где n – количество элементов множества.
Для наглядного представления множеств и отношений между ними используются диаграммы Эйлера-Венна. Исходные множества обозначаются кругами. Элементы множества обозначаются точками внутри круга, если они принадлежат множеству и точками вне круга, если они множеству не принадлежат. Множество, содержащее все множества, обозначается прямоугольником и называется универсальным множеством (U).
Примеры:
Упражения:
1. Приведите примеры множеств, составленных из объектов следующих видов:
а) неодушевленных предметов;
б) животных;
в) растений;
г) геометрических фигур;
д) населенных пунктов;
е) водоемов;
ж) политических деятелей.
2. Назовите элементы, принадлежащие множеству:
а) студентов вашей группы;
б) предметов, изучаемых в I семестре вашей специальности;
в) всех частей света;
г) субъектов федерации, входящих в Российскую Федерацию.
3. Пусть А – множество многоугольников. Принадлежат ли этому множеству:
а) восьмиугольник;
б) параллелограмм;
в) отрезок;
г) параллелепипед;
д) круг;
е) полукруг?
4. Из каких элементов состоят следующие множества:
а) множество трехзначных чисел, составленных с помощью цифр 1 и 3;
б) множество трехзначных чисел, составленных с помощью цифр 1, 3, 5, причем так, что никакие две цифры не встречаются дважды;
в) множество трехзначных чисел, составленных из цифр 1, 3, 5 так, что любые две соседние цифры различны;
г) множество трехзначных чисел, сумма цифр которых равна 5.
д) множество делителей числа 36. Можно ли задать таким образом множество кратных чисел числу 36?
5.
6.
7.
8.
9.
10.
11.
12.
Домашнее задание:
1. Выпишите все подмножества множества А={1; 2; 3}, B={в; о; д; а
2. Укажите множество элементов множества, соответствующее записи. Выпишите один элемент, принадлежащий множеству, и один элемент, не принадлежащий этому множеству: