В ряде реальных экономических и производственных задач необходимо учитывать изменение моделируемого процесса во вре­мени и влияние времени на критерий оптимальности. Для реше­ния указанных задач используется метод динамического планиро­вания (динамическое программирование). Этот метод более сложен по сравнению с методами расчета статических оптимиза­ционных задач, изложенных выше. Также не простым делом явля­ется процесс построения для реальной задачи математической модели динамического программирования.

Пусть рассматривается задача, распадающаяся на т шагов или этапов, например планирование деятельности предприятия на несколько лет, поэтапное планирование инвестиций, управление производственными мощностями в течение длительного срока. Показатель эффективности задачи в целом обозначим через W, а показатели эффективности на отдельных шагах — через 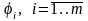. Если W обладает свойством аддитивности, т.е. 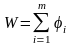, (2.9) то можно найти оптимальное решение задачи методом динамичес­кого программирования.

Таким образом, динамическое программирование — это ме­тод оптимизации многошаговых или многоэтапных процессов, кри­терий эффективности которых обладает свойством (2.9). В зада­чах динамического программирования критерий эффективности называется выигрышем. Данные процессы управляемые, и от пра­вильного выбора управления зависит величина выигрыша.

Переменную х_i, от которой зависят выиг­рыш на i-м шаге и, следовательно, выигрыш в целом, называют шаговым управлением, .

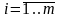Управлением процесса в целом Х называется последовательность шаговых управлений Х = (x₁, х₂,..., х_i ,..., х_m).

Оптимальным управлением х* считают такое значение управления х, при котором значение W(x*) является максимальным (или минимальным, если требуется уменьшить проигрыш): W* = W(x*) = max {W(x)}, xX, где Х – область допустимых решений. Оптимальное управление х* определяется последовательностью оптимальных шаговых управлений х*=(х₁*, х₂*, …, х_m*).

В основе метода динамического программирования лежит принцип оптимальности Беллмана, формулирующийся следующим образом: управление на каждом шаге надо выбирать так, чтобы оптимальной была сумма выигрышей на всех оставшихся до конца процесса шагах, включая выигрыш на данном шаге.

При решении задачи динамического программирования на каждом шаге выбирается управление, кото­рое должно привести к оптимальному выигрышу, т.е. в многошаговых процессах все шаги зависят друг от друга, и, следовательно, управление на каждом конкретном шаге надо выбирать с учетом его будущих воздействий на весь процесс.

Другой момент, который следует учитывать при выборе управ­ления на данном шаге, — это возможные варианты окончания предыдущего шага. Эти варианты определяют состояние процес­са. Таким образом, при выборе шагового уп­равления необходимо учитывать: 1) возможные исходы предыду­щего шага и 2) влияние управления на все оставшиеся до конца процесса шаги.

---

В задачах динамического программирования первый пункт учитывают, делая на каждом шаге условные предположения о воз­можных вариантах окончания предыдущего шага и проводя для каждого из вариантов условную оптимизацию. Выполнение вто­рого пункта обеспечивается тем, что в задачах динамического про­граммирования условная оптимизация проводится от конца про­цесса к началу. Сперва оптимизируется последний m-й шаг, на котором не надо учитывать возможные воздействия выбранного управления х_m на все последующие шаги, так как эти шаги просто отсутствуют. Делая предположения об условиях окончания (m-1)-го шага, для каждого из них проводят условную оптимизацию m-го шага и определяют условное оптимальное управление х_m. Анало­гично поступают для (m-l)-ro шага, делая предположения об ис­ходах окончания (m-2)-ro шага и определяя условное оптималь­ное управление на (m-1)-м шаге, приносящее оптимальный выигрыш на двух последних шагах — (m-1)-м и m-м. Так же дей­ствуют на всех остальных шагах до первого. На первом шаге, как правило, не надо делать условных предположений, так как состоя­ние системы перед первым шагом обычно известно.

Для этого состояния выбирают оптимальное шаговое управле­ние, обеспечивающее оптимальный выигрыш на первом и всех последующих шагах. Это управление является безусловным опти­мальным управлением на первом шаге и, зная его, определяются оптимальное значение выигрыша и безусловные оптимальные уп­равления на всех шагах.

Для написания математической постановки задачи динамического программирования введём следующие обозначения:

s — состояние процесса;

S_j — множество возможных состояний процесса перед i-м шагом;

W_i — выигрыш с i-го шага до конца процесса, 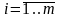. Можно определить следующие основные этапы составления математической модели задачи динамического программирования.

1). Разбиение задачи на шаги (этапы). Шаг не должен быть слиш­ком мелким, чтобы не проводить лишних расчетов и не должен быть слишком большим, усложняющим процесс шаговой опти­мизации.

2). Выбор переменных, характеризующих состояние s моделируе­мого процесса перед каждым шагом, и выявление налагаемых на них ограничений.

3). Определение множества шаговых управлений х_i, 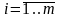и на­лагаемых на них ограничений, т.е. области допустимых управ­лений X.

4). Определение выигрыша  (s, x_i), который принесёт на i-м шаге управление x_i, если система перед этим находилась в состоянии s.

5). Определение состояния s', в которое переходит система из со-
стояния s под влиянием управления х_i: ,

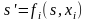где f_i— функция перехода на i-м шаге из состояния s в состо­яние s'.

6). Составление уравнения, определяющего условный оптималь-
ный выигрыш на последнем шаге, для состояния s моделируе-
мого процесса: .

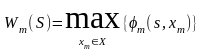7). Составление основного функционального уравнения динами-
ческого программирования, определяющего условный опти-
мальный выигрыш для данного состояния s с i-го шага и до кон-
ца процесса через уже известный условный оптимальный
выигрыш с (i+1)-го шага и до конца:

---

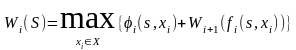(2.10)

В уравнении (2.10) в уже известную функцию W_i+1(s), харак­теризующую условный оптимальный выигрыш с (i+1)-го шага до конца процесса, вместо состояния s подставлено новое состояние s' = f_i(s, x_i), в которое система переходит на i-м шаге под влияни­ем управления х_i.

Заметим, что структура модели динамического программиро­вания отличается от статической модели линейного программи­рования. Действительно, в моделях линейного программирования управляющие переменные — это одновременно и переменные со­стояния моделируемого процесса, а в динамических моделях от­дельно вводятся переменные управления х_i, и переменные, харак­теризующие изменение состояния s под влиянием управления. Таким образом, структура динамических моделей более сложная, что естественно, так как в этих моделях дополнительно учитыва­ется фактор времени.

Основными метода решения задач динамического программирования является метод комбинаторного перебора возможных вариантов решений и аналогичный по идеологии – метод ветвей и границ.

Процесс разработки меню для больных сахарным диабетом является дискретным управляемым процессом, т.к. набор блюд является дискретным, а его подбор может осуществляться в течение дня, недели, месяца последовательно во времени в соответствии с множеством критериев. Однако, для разработки оптимального меню больных сахарным диабетом нецелесообразно применять модели динамического программирования, т.к. достаточно просто динамику подбора блюд в соответствии с гликемическим индексом, углеводосодержанием (хлебными единицами) и т.д. заменить на «статический план потребления» блюд за сутки, за неделю, за месяц, выполняя формирование оптимального меню на конкретный временной интервал без его корректировки в течение выбранного интервала. Что позволит упростить решение задачи оптимизации рациона и меню больных сахарным диабетом.

Графические модели используются тогда, когда задачу удобно представить в виде графической структуры. К таким классам задач относятся транспортные задачи, задачи оптимизации на графах и сетях, такие как, нахождение оптимального маршрута, прохождение заданного маршрута с минимальным временем, задачи обхода вершин деревьев и т.д. Для решения указанных задач применяют специальные методы и алгоритмы, реализуемые на ЭВМ, в большей степени имеющие отношение не к математическому моделированию, а к алгоритмизации и программированию.

---

Смотрите также файлы

• 3.3. Дополнение к классификации видов моделирования систем.docx

• 3.2. Классификация видов моделирования систем.docx

• 3.1. Классификация видов моделирования систем и моделей.doc

• 2.4. Принципы и структура системного анализа.docx

• 2.3. Термины и определения системного анализа и теории систем.docx