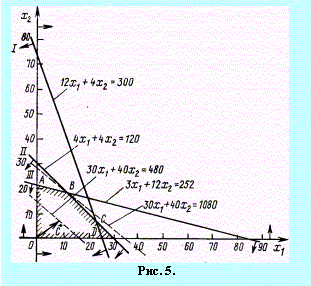
Найдем, например, полуплоскость, определяемую неравенством  Для этого, построив прямую  (на рис. 5 эта прямая I), возьмем какую-нибудь точку, принадлежащую одной из двух полученных полуплоскостей, например точку О(0; 0). Координаты этой точки удовлетворяют неравенству  значит, полуплоскость, которой принадлежит точка О(0; 0), определяется неравенством Это и показано стрелками на рис. 5.

Пересечение полученных полуплоскостей и определяет многоугольник решений данной задачи.

Как видно из рис. 5, многоугольником решений является пятиугольник OABCD. Координаты любой точки, принадлежащей этому пятиугольнику, удовлетворяют данной системе неравенств и условию неотрицательности переменных. Поэтому сформулированная задача будет решена, если мы сможем найти точку, принадлежащую пятиугольнику OABCD, в которой функция F принимает максимальное значение. Чтобы найти указанную точку, построим вектор  и прямую  где h – некоторая постоянная такая, что прямая  имеет общие точки с многоугольником решений. Положим, например, h = 480 и построим прямую  (рис. 5).

Если теперь взять какую-нибудь точку, принадлежащую построенной прямой и многоугольнику решений, то ее координаты определяют такой план производства изделий А и В, при котором прибыль от их реализации равна 480 руб. Далее, полагая h равным некоторому числу, большему чем 480, мы будем получать различные параллельные прямые. Если они имеют общие точки с многоугольником решений, то эти точки определяют планы производства изделий А и В, при которых прибыль от их реализации превзойдет 480 руб.

Перемещая построенную прямую  в направлении вектора  видим, что последней общей точкой ее с многоугольником решений задачи служит точка В. Координаты этой точки и определяют план выпуска изделий А и В, при котором прибыль от их реализации является максимальной.

Найдем координаты точки В как точки пересечения прямых II и III. Следовательно, ее координаты удовлетворяют уравнениям этих прямых

Решив эту систему уравнений, получим  Следовательно, если предприятие изготовит 12 изделий вида А и 18 изделий вида В, то оно получит максимальную прибыль, равную 

Пример 8.

Найти максимум и минимум функции  при условиях

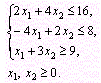
Решение. Построим многоугольник решений. Для этого в неравенствах системы ограничений и условиях неотрицательности переменных знаки неравенств заменим на знаки точных равенств:

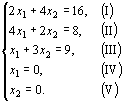
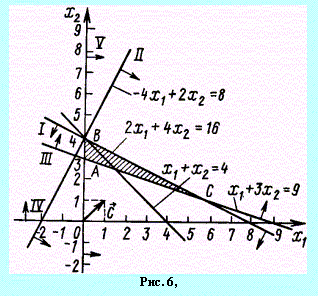
Построив полученные прямые, найдем соответствующие полуплоскости и их пересечение (рис. 6).

Как видно из рис. 6, многоугольником решений задачи является треугольник АВС. Координаты точек этого треугольника удовлетворяют условию неотрицательности и неравенствам системы ограничений задачи. Следовательно, задача будет решена, если среди точек треугольникаАВС найти такие, в которых функция  принимает максимальное и минимальное значения. Для нахождения этих точек построимпрямую  (число 4 взято произвольно) и вектор 

---

Передвигая данную прямую параллельно самой себе в направлении вектора  видим, что ее последней общей точкой с многоугольником решений задачи является точка С. Следовательно, в этой точке функция F принимает максимальное значение. Так как С – точка пересечения прямых I и II, то ее координаты удовлетворяют уравнениям этих прямых:

Решив эту систему уравнений, получим  Таким образом, максимальное значение функции 

Для нахождения минимального значения целевой функции задачи передвигаем прямую  в направлении, противоположном направлению вектора  В этом случае, как видно из рис. 6, последней общей точкой прямой с многоугольником решений задачи является точка А. Следовательно, в этой точке функция F принимает минимальное значение. Для определения координат точки А решаем систему уравнений

откуда  Подставляя найденные значения переменных в целевую функцию, получим 

---

Смотрите также файлы

• 4.2. Принципы и подходы к построению математических моделей. Этапы построения математических моделей.docx

• 4.1. Классификация математических моделей.docx

• 3.3. Дополнение к классификации видов моделирования систем.docx

• 3.2. Классификация видов моделирования систем.docx

• 3.1. Классификация видов моделирования систем и моделей.doc