Тема: Линейное программирование. Общая постановка задачи. Методы решения задач линейного программирования. Двойственная задача линейного програм­ми­рования.

Примеры задач, относящихся к классу задач линейного программирования: задача планирования производства при ограниченных ресурсах, задача о составлении оп­ти­­мального рациона, задача о загрузке производственного оборудования, задача о раскрое материалов и другие.

Преобразование задачи одной из имеющихся постановок в другие формы. Базисные и свободные переменные. Многогранник ограничений, его определение и пример построения для задач малой размерности. Целевая функция, её гради­ент, линии уровня. Экономический смысл градиента, его изображение в задачах ЛП малой размер­ности.

Общая постановка задачи линейного програм­ми­ро­ва­ния:

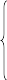
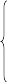
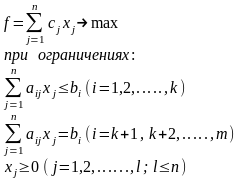или

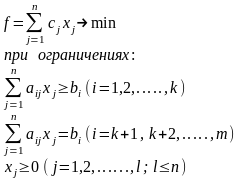
Задача линейного программирования в стандартной постановке (в ней все огра­ни­чения имеют вид неравенств, все неизвестные имеют неотрицательные значения):

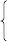
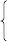
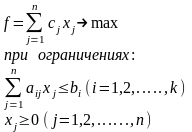или

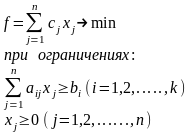
Каноническая задача линейного программирования (система ограничений состоит из уравнений, все переменные неотрицательны):

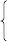
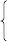
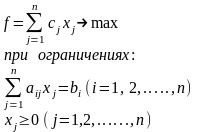или

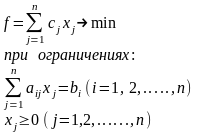
Задача линейного программирования как задача выпук­лого анализа. Обо­сно­вание свойств задачи линейного программирования и воз­мож­ности её решения (теоремы о выпуклости множества допустимых решений зада­чи линей­ного про­грам­­мирования (ЛП) и существовании её оптимального ре­ше­ния).

Геомет­рический метод решения задач линейного программирования, его применимость для решения задач ЛП малой размерности. Симплекс – метод как универсальный метод решения любых задач ЛП. Аналитический и табличный варианты алгоритма симплекс – метода. Особые случаи, возникающие при реше­нии задач ЛП: неединственность оптимального решения (оптимальное решение достигается в любой точке некоторой грани многогранника ограничений), появление вырожденных базисных решений, приводящих к зацикливанию, реше­ние такой проблемы. Метод искусственного базиса для решения задач ЛП.

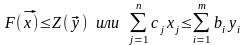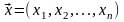Существование для каждой задачи ЛП двойственной или сопряжённой. Примеры существования двойственных задач для конкретных примеров экономических за­дач. Взаимно двойственные задачи линейного программирования и их свойства. Алгоритм составления двойственной задачи по данной прямой. Основное нера­венство теории двойственности: , где и 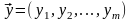- допустимые решения исходной и двойственной задач. Достаточный признак оптимальности (теорема).

Первая (основная) теорема двойственности: если одна из взаимно двойственных задач имеет оптимальное решение, то его имеет и другая: F_max = Z_min. Экономический смысл первой теоремы двойственности.

Вторая теорема двойственности: компоненты оптимального решения двойственной задачи равны абсолютным значениям коэффициентов при соответствующих переменных линейной функции исходной задачи, выраженной через неосновные переменные её оптимального решения.

---

Третья теорема двойственности: компоненты оптимального решения двойственной задачи равны значениям частных производных линейной функции F_max(b₁,b₂,…,b_m) по соответствующему аргументу (b_i, i = 1, 2,…,m).

---

Смотрите также файлы

• 5.1. Математическая постановка и методы решения задач линейного программирования.docx

• 4.2. Принципы и подходы к построению математических моделей. Этапы построения математических моделей.docx

• 4.1. Классификация математических моделей.docx

• 3.3. Дополнение к классификации видов моделирования систем.docx

• 3.2. Классификация видов моделирования систем.docx