Файл: Информатика Щапов Щапова.pdf

51 

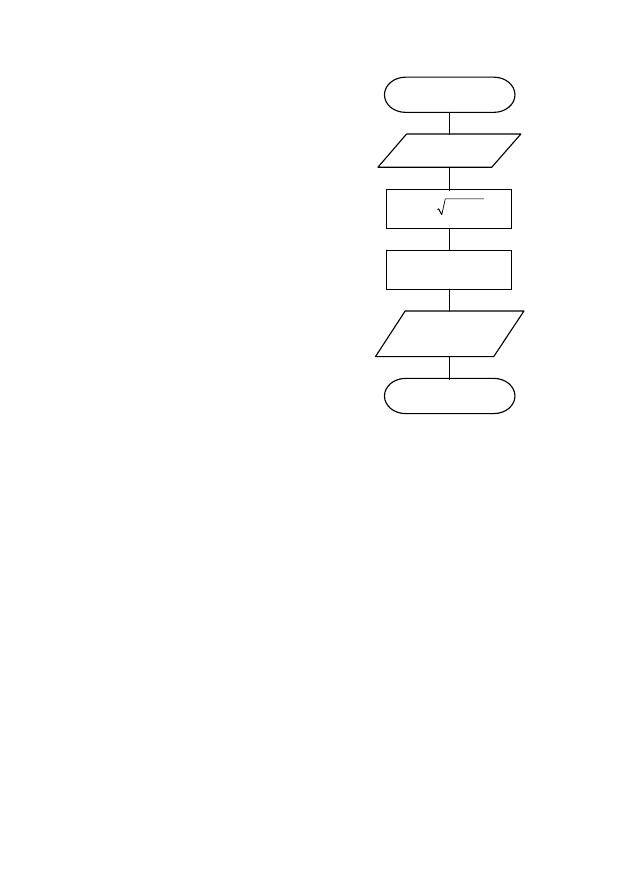
Пример.  Даны  катеты  прямо-

угольного  треугольника  a,  b.  Найти 
его  гипотенузу  c  и  площадь  s. 
Блок-схема  алгоритма  приведена  на 
рис. 4. 

Алгоритмы  разветвляющейся 

структуры.  Разветвляющимся  (вет-
вящимся) называется алгоритм, кото-
рый в зависимости от исходных дан-
ных или промежуточных результатов 
вычисления  реализуется  по  одному 
из нескольких заранее предусмотрен-
ных направлений. Такие направления 
называются  ветвями  вычислений. 
Выбор той или иной ветви осуществ-
ляется  в  зависимости  от  результата 
проверки  условия.  В  каждом  кон-
кретном случае алгоритм реализуется 
только по одной ветви, а выполнение 
остальных исключается. 

Рис. 4. Пример линейного 

алгоритма

В  качестве  примера  использования  ветвлений  рассмотрим 

составление  алгоритма  для  вычисления  значения  функции  f(x) 
в зависимости от конкретных значений x, a, b: 

2

2

при

1,

при 1

4,

при

4.

x a

x

f

x a b

x

x b

x

 







 

 



 





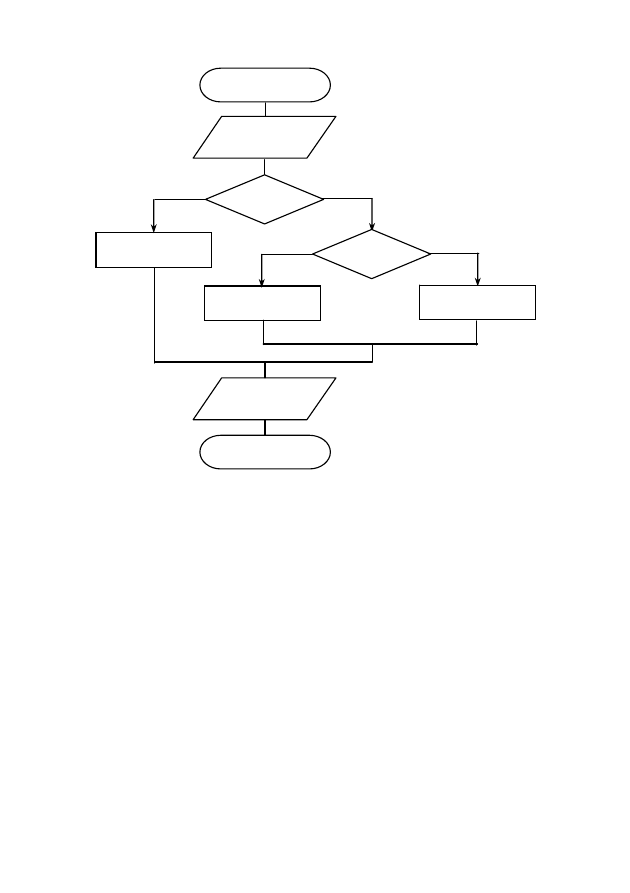
Блок-схема  алгоритма  решения  этой  задачи  приведена 

на рис. 5. 

Алгоритмы циклической структуры. Алгоритмы, в кото-

рых отдельные действия многократно повторяются, называются 
циклическими.  Типовые  алгоритмические  структуры,  реализую-
щие  циклический  вычислительный  процесс,  приведены  на 
рис. 3. Циклический алгоритм состоит из подготовки цикла, тела 
цикла и условия повторения цикла. 

Начало 

Ввод a, b 

Вывод 

c, s 

Конец 

2

2

c

a

b





 s = a



b/2 

52 

Рис. 5. Пример разветвляющегося алгоритма 

Характерной  для  этого  класса  вычислительных  процессов 

является задача табулирования функции, т.е. вычисления значе-
ний функции y = f(x) на отрезке [x

н

, x

k

] с шагом 

х (рис. 6). 

Примером алгоритма циклической  структуры является 

задача вычисления суммы и произведения. 

Если  необходимо  вычислить  сумму  значений  некоторой 

функции y = f(x) при различных значениях аргумента, то целесо-
образно  организовать  цикл,  в  котором  не  только  вычисляются 
текущие значения функции, но и накапливается их сумма путем 
прибавления  полученного  слагаемого  к  сумме  предыдущих. 
Формула для вычисления суммы имеет следующий вид: 

1

i

i

i

S

S

y





 . 

Начало

Ввод 

a, b, x 

Вывод 

x, f 

Конец

f = x + b

2

f = x + a

2 

x 

 1 

нет

да

x 

 4 

нет

да

f = x – a



b 

53 

При первом выполнении цикла вычисляется значение 

1

0

1

S

S

y



 , 

которое  должно  быть  равно  y

1

.  Поэтому  перед  циклом  на-

чальному  значению  суммы  следует  присвоить  значение  ноль,  
т.е. S

0

 = 0. 

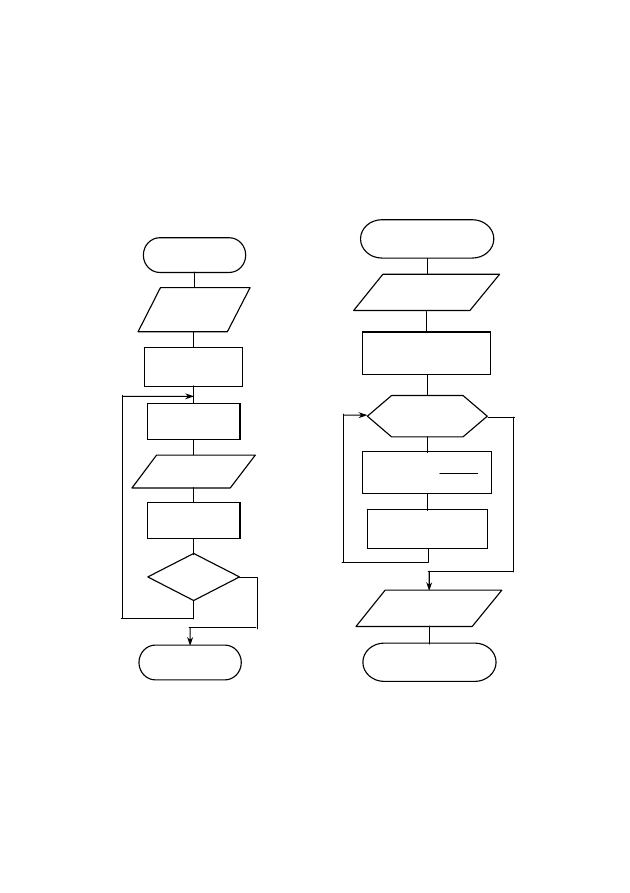
Рис. 6. Блок-схема алгоритма  

табулирования функции 
(циклический алгоритм)

Рис. 7. Блок-схема алгоритма  

вычисления суммы членов ряда  

(циклический алгоритм)

Начало 

Ввод х 

S = 0 

n = 1, 6

y = 

2

1

1

2

( 1)

4

1

n

n

x

n











S = S + y 

Вывод S 

Конец 

Начало 

Ввод 

х

н

, х

к

, 

х 

х = х

н

х > х

к 

х = х + 

х 

нет 

да 

y = f(x) 

Вывод x, y 

Конец 

54 

Аналогично  вычисляется  и  произведение,  с  той  лишь  раз-

ницей, что для его накопления используется формула 

1

i

i

i

P

P

y





 , 

а начальное значение произведения должно быть равно единице, 
т.е. P

0

 = 1. 

Пример. Вычислить  S

   

2

1

6

1

2

1

( 1)

,

0,3

4

1

n

n

n

x

x

n

















. Блок-

схема  алгоритма  решения  этой  задачи  представлена  на  рис. 7. 
Так  как  результат  решения  представляет  собой  одно  число,  то 
блок вывода результата стоит за циклом и результаты печатают-
ся один раз. 

Циклические  алгоритмы  с  неизвестным  числом  повто-

рений.  Циклические  процессы,  в  которых  заранее  неизвестно 
число  повторений,  а  проверка  выхода  из  цикла  ведется  по  дос-
тижении  требуемой  точности,  называются  итерационными. 
Большинство  численных  (приближенных)  методов  решения 
многих математических задач являются итерационными: вычис-
ления проводятся до тех пор, пока не будет достигнута заданная 
точность, при этом заранее не известно, сколько необходимо для 
этого совершить циклических операций. Аналогичная задача воз-
никает  при  вычислении  сумм  рядов  с  бесконечным  числом  сла-
гаемых. 

Пример.  Вычислить  сумму  членов  сходящегося  ряда 

1

,

1,1

k

k

k

x

S

x

k











 с заданной точностью 

 = 10

–3

. 

Вычисление суммы прекращается, если очередной член ря-

да  y

k

  становится  меньше  заданной  точности 

,  т.е.  выполнится 

условие 

k

k

x

k

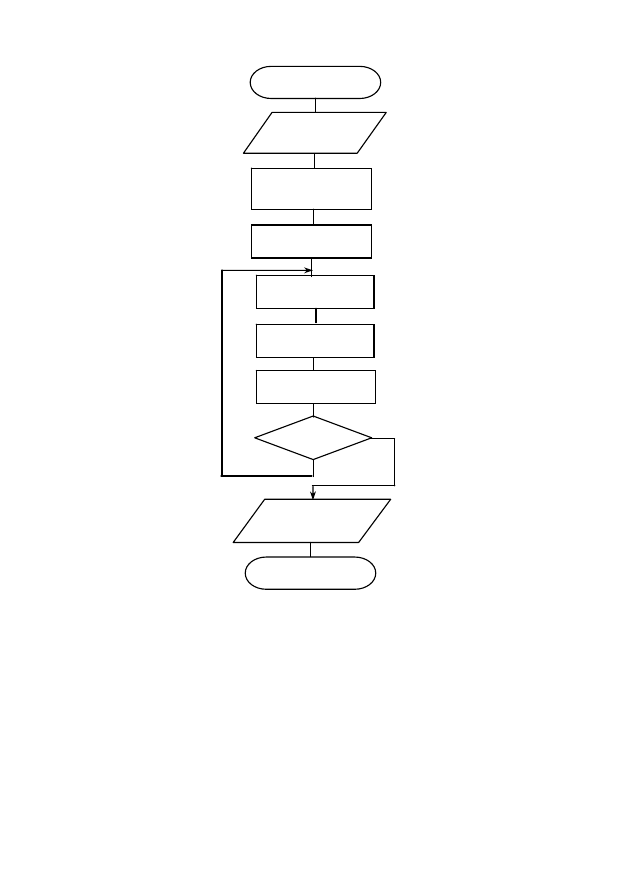
  .  Блок-схема  алгоритма  решения  этой  задачи 

представлена на рис. 8. Блок вывода результата содержит также 
переменную k – количество членов ряда, вошедших в сумму. 

55 

Рис. 8. Блок-схема итерационного  

алгоритма вычисления суммы сходящегося ряда 

Вложенные  циклы.  Существует  возможность  организо-

вать  цикл  внутри  тела  другого  цикла.  Такой  цикл  называется 
вложенным циклом. 

При этом цикл, содержащий в себе другой, называют внеш-

ним,  а  цикл,  находящийся  в  теле  первого, – внутренним  (вло-
женным).  Внутрь  вложенного  цикла,  в  свою  очередь,  может 
быть  вложен  еще  один  цикл,  образуя  следующий  уровень  вло-
женности и т.д. 

Начало

Ввод 

х, 

 

s = 0 
k = 1 

|y| < 



s = s + y 

нет 

да 

Вывод 

 s, k – 1 

Конец

y = x

k

/k

k

y = x

k

/k

k

k = k + 1