Файл: 5.4. Некоторые виды задач линейного программирования (транспортная задача, задача о назначениях).docx
ВУЗ: Смоленский областной казачий институт промышленных технологий и бизнеса
Категория: Лекция
Дисциплина: Моделирование систем
Добавлен: 19.11.2018
Просмотров: 399
Скачиваний: 6
Тема: Прикладные модели, относящиеся к задачам линейного программирования. Задача нахождения оптимального плана. Транспортная задача. Задача о назначениях.
Задача нахождения оптимального производственного плана. Для изготовления различных видов изделий используются разные ресурсы. Общие запасы каждого ресурса, количество ресурсов каждого вида, прибыль, получаемая от реализации одного изделия определённого вида заданы. Нужно составить план производства изделий, обеспечивающий максимальную суммарную прибыль от их реализации.
Этапы построения экономико - математической модели:
-
целью является максимизация прибыли;
-
для формулировки задачи вводим следующие условные обозначения:
n – число различных видов изделий; m – число различных типов ресурсов;
bi
- запас ресурса i
– го типа,
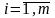 ;
aij
– количество ресурсов i-го
типа, необходимых для изготовления
одного изделия j-го
вида,
;
aij
– количество ресурсов i-го
типа, необходимых для изготовления
одного изделия j-го
вида,
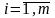 ,
,
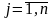 ;
pj
– прибыль от реализации одного изделия
j-го
вида;
;
pj
– прибыль от реализации одного изделия
j-го
вида;
-
управляющие переменные xj,
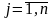 -
число изделий j-го
вида;
-
число изделий j-го
вида; -
о
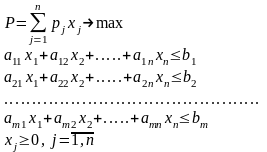 граничения
задачи – ограничения по ресурсам и
условия неотрицательности управляющих
переменных.
граничения
задачи – ограничения по ресурсам и
условия неотрицательности управляющих
переменных.
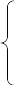
Постановка
транспортной задачи:
задано m
поставщиков продукции одного вида и n
потребителей, предложение каждого i-го
поставщика составляет ai
– единиц,
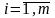 ;
спрос каждого j-го
потребителя - bj
единиц,
;
спрос каждого j-го
потребителя - bj
единиц,
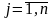 ;
тарифы перевозок равны сij,
;
тарифы перевозок равны сij,
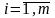 ,
,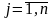 .
Найти объёмы перевозок для каждой
пары «Поставщик - потребитель» так,
чтобы 1) мощности всех поставщиков были
реализованы, 2) спросы всех потребителей
были удовлетворены, 3) суммарные затраты
на перевозку были бы минимальными. В
качестве переменных в данной задаче
выступают xij
– количество продукции, перевозимой
от i-го
поставщика j-му
потребителю
.
Найти объёмы перевозок для каждой
пары «Поставщик - потребитель» так,
чтобы 1) мощности всех поставщиков были
реализованы, 2) спросы всех потребителей
были удовлетворены, 3) суммарные затраты
на перевозку были бы минимальными. В
качестве переменных в данной задаче
выступают xij
– количество продукции, перевозимой
от i-го
поставщика j-му
потребителю
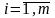 ,
,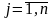 .
Формальная запись транспортной задачи:
.
Формальная запись транспортной задачи:
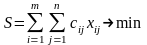

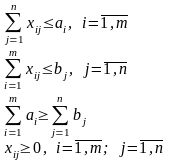
Методы нахождения начального решения транспортной задачи: метод «северо-западного угла», метод минимального элемента, метод Фогеля. Нахождение оптимального плана транспортной задачи. Метод потенциалов.
Общая формулировка
задачи о назначениях:
имеется n
работ и n
кандидатов для их выполнения. Затраты
i-го
кандидата на выполнение j-й
работы равны сij
(i,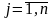 ).
Каждый кандидат может быть назначен
только на одну работу, а каждая работа
может быть выполнена только одним
кандидатом. Требуется найти назначение
кандидатов на работы, при котором
суммарные затраты на выполнение
работ минимальны. Пусть xij
– переменная, значение которой равно
1, если i-й
кандидат выполняет j-ю
работу и 0 – в противном случае. Тогда
условие, что кандидат выполняет только
одну работу имеет вид:
).
Каждый кандидат может быть назначен
только на одну работу, а каждая работа
может быть выполнена только одним
кандидатом. Требуется найти назначение
кандидатов на работы, при котором
суммарные затраты на выполнение
работ минимальны. Пусть xij
– переменная, значение которой равно
1, если i-й
кандидат выполняет j-ю
работу и 0 – в противном случае. Тогда
условие, что кандидат выполняет только
одну работу имеет вид:
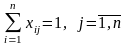 .
Условие о том, что каждая работа может
выполняться только одним кандидатом
можно представить в виде:
.
Условие о том, что каждая работа может
выполняться только одним кандидатом
можно представить в виде:
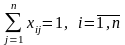 .
.

выглядит следующим образом:
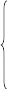
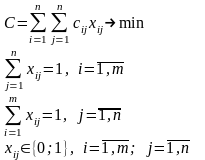
Методы решения задачи о назначениях: симплекс – метод, метод потенциалов, венгерский метод, пакет MS Excel «Поиск решения». Алгоритм венгерского метода решения задачи о назначениях. Применение рассмотренного алгоритма для решения задач о назначениях произвольной размерности.