ВУЗ: Смоленский областной казачий институт промышленных технологий и бизнеса
Категория: Лекция
Дисциплина: Моделирование систем
Добавлен: 19.11.2018
Просмотров: 287
Скачиваний: 11
Тема: Линейное программирование. Транспортная задача. Метод потенциалов.
Задание: составить оптимальный план распределения поставок. Начальный базисный план перевозок можно сделать любым известным способом. Стоимость перевозки единицы груза, а также потребности и наличие груза даны в таблице.
|
Поставщики/ Потребители |
20 |
110 |
40 |
110 |
|
60 |
1 |
2 |
5 |
3 |
|
120 |
1 |
6 |
5 |
2 |
|
100 |
6 |
3 |
7 |
4 |
Решение
Методом минимального элемента составляем начальный план перевозок. Согласно этому методу, грузы распределяются в первую очередь в те клетки, в которых находится минимальный тариф перевозок сij. Далее поставки распределяются в незанятые клетки с наименьшими тарифами с учетом оставшихся запасов у поставщиков и удовлетворения спроса потребителей. Процесс продолжается до тех пор, пока все грузы от поставщиков не будут вывезены, а потребители не будут удовлетворены. При распределении грузов может оказаться, что количество занятых клеток меньше, чем m+n-1. В этом случае недостающее их число заполняется клетками с нулевыми поставками, такие клетки называют условно занятыми.
Нулевые поставки помещают в незанятые клетки с учетом наименьшего тарифа таким образом, чтобы в каждых строке и столбце было не менее чем по одной занятой клетки.
Так как
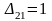 (минимальный элемент), то в него помещаем
20, оставшиеся ячейки в первом столбце
будут пустыми так как весь груз на данном
объекте распределен. В ячейку
(минимальный элемент), то в него помещаем
20, оставшиеся ячейки в первом столбце
будут пустыми так как весь груз на данном
объекте распределен. В ячейку
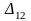 помещаем 60, а в ячейку
помещаем 60, а в ячейку
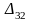 помещаем 50, так как оценка стоимости в
данной клетке меньше чем в ячейке
помещаем 50, так как оценка стоимости в
данной клетке меньше чем в ячейке
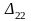 .
В ячейку
.
В ячейку
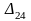 помещаем 100, так как в этой ячейке
находится минимальная стоимость из
всех оставшихся. На данном объекте
осталось 10 единиц груза, его помещаем
в ячейку
помещаем 100, так как в этой ячейке
находится минимальная стоимость из
всех оставшихся. На данном объекте
осталось 10 единиц груза, его помещаем
в ячейку
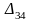 , так как это последний оставшийся
потребитель, который готов приобрести
последний оставшийся груз. 40 помещаем
в ячейку
, так как это последний оставшийся
потребитель, который готов приобрести
последний оставшийся груз. 40 помещаем
в ячейку
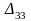 ,
так как 40 единиц груза может приобрести
3-ий потребитель.
,
так как 40 единиц груза может приобрести
3-ий потребитель.
|
Поставщики/ Потребители |
20 |
110 |
40 |
110 |
|
60 |
1 |
2 60 |
5 |
3 |
|
120 |
1 20 |
6 |
5 |
2 100 |
|
100 |
6 |
3 50 |
7 40 |
4 10 |
Для каждой заполненной клетки записываем уравнение потенциалов:
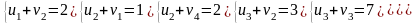 ,
где ui
– номер строки, а vj-
номер столбца
,
где ui
– номер строки, а vj-
номер столбца
Решая систему уравнений получаем:

Составим разности потенциалов для свободных клеток:
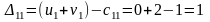
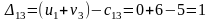
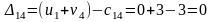
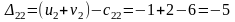
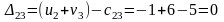
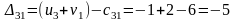
Так как
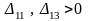 ,
то опорное решение не является оптимальным
и его можно улучшить, перейдя от одного
опорного решения к другому.
,
то опорное решение не является оптимальным
и его можно улучшить, перейдя от одного
опорного решения к другому.
Для свободной
клетки с
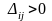 строится цикл, все вершины которого
кроме одной находятся в занятых клетках;
углы прямые, число вершин четное. Около
свободной клетки цикла ставится знак
(+), затем поочередно проставляют знаки
(-) и (+). У вершин со знаком (-) выбирают
минимальный груз, его прибавляют к
грузам, стоящим у вершин со знаком (+), и
отнимают от грузов у вершин со знаком
(-). В результате перераспределения груза
получим новое опорное решение. Это
решение проверяем на оптимальность и
т.д. до тех пор, пока не получим оптимальное
решение.
строится цикл, все вершины которого
кроме одной находятся в занятых клетках;
углы прямые, число вершин четное. Около
свободной клетки цикла ставится знак
(+), затем поочередно проставляют знаки
(-) и (+). У вершин со знаком (-) выбирают
минимальный груз, его прибавляют к
грузам, стоящим у вершин со знаком (+), и
отнимают от грузов у вершин со знаком
(-). В результате перераспределения груза
получим новое опорное решение. Это
решение проверяем на оптимальность и
т.д. до тех пор, пока не получим оптимальное
решение.
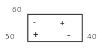 Для
свободной клетки (1;3), имеющей положительную
оценку (
Для
свободной клетки (1;3), имеющей положительную
оценку (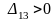 )
строится цикл.
)
строится цикл.
 У
вершин со знаком (-) выбираем минимальный
груз, он равен 40. Его прибавляем к грузам,
стоящих у положительных вершин, и
отнимаем от грузов, стоящих у отрицательных
вершин. Получаем новый цикл:
У
вершин со знаком (-) выбираем минимальный
груз, он равен 40. Его прибавляем к грузам,
стоящих у положительных вершин, и
отнимаем от грузов, стоящих у отрицательных
вершин. Получаем новый цикл:
После перераспределения груза в пределах цикла имеем следующую транспортную таблицу. Транспортная таблица не является окончательной, поэтому выполняем дальнейшие расчёты.
|
Поставщики/ Потребители |
20 |
110 |
40 |
110 |
|
60 |
1 |
2 20 |
5 40 |
3 |
|
120 |
1 20 |
6 |
5 |
2 100 |
|
100 |
6 |
3 90 |
7 |
4 10 |
Для каждой заполненной клетки записываем уравнение потенциалов:
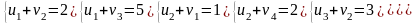 ,
где ui
– номер строки, а vj-
номер столбца
,
где ui
– номер строки, а vj-
номер столбца
Решая систему уравнений получаем:

Составляем разности потенциалов для свободных клеток:
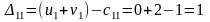
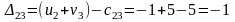
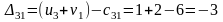
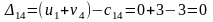
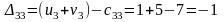
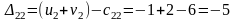
20
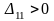 ,
то опорное решение не является оптимальным
и его можно улучшить, перейдя от одного
опорного решения к другому. Строим цикл
для ячейки
,
то опорное решение не является оптимальным
и его можно улучшить, перейдя от одного
опорного решения к другому. Строим цикл
для ячейки
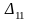 .
.

90
Имеем следующее распределение поставок:
|
Поставщики/ Потребители |
20 |
110 |
40 |
110 |
|
60 |
1 10 |
2 10 |
5 40 |
3 |
|
120 |
1 10 |
6 |
5 |
2 110 |
|
100 |
6 |
3 100 |
7 |
4 |
Для каждой заполненной клетки записываем уравнение потенциалов:
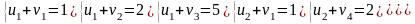 ,
где ui
– номер строки, а vj-
номер столбца
,
где ui
– номер строки, а vj-
номер столбца
Решая систему уравнений получаем:

Составляем разности потенциалов для свободных клеток:
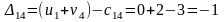
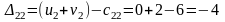
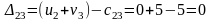
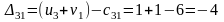
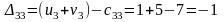
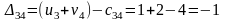
Получили, что все оценки свободных клеток не положительные, следовательно, найденное решение оптимальное. Найденный план оптимальный, но не единственный, так как присутствует нулевая оценка.

Стоимость перевозок равна:
F=1*10+2*10+5*40+1*10+2*110+3*100=10+20+200+10+220+300=760
Ответ:

Стоимость перевозок равна: F=760.