Целочисленное программирование

Целочисленное программирование – один из наиболее молодых, перспективных и быстро развивающихся разделов математического программирования. Можно перечислить большое количество разнообразных задач планирования экономики, организации производства, исследования конфликтных  ситуаций, синтеза схем автоматического регулирования, которые формально сводятся к выбору лучших, в некотором смысле, значений параметров из определенной дискретной совокупности заданных величин. К ним можно отнести и экстремальные комбинаторные задачи, возникающие в различных разделах дискретной математики.

Задачи и методы, относящиеся к перечисленному кругу вопросов, в литературе именуются по-разному. Наибольшее распространение получил термин «целочисленное программирование», однако встречаются и такие как «дискретное программирование», реже «комбинаторное (или диофантово) программирование».

Наиболее изученными задачами этого класса являются целочисленные задачи линейного программирования, в которых на все переменные (или на их часть) наложено дополнительное требование целочисленности. От них принято отличать так называемые дискретные задачи линейного программирования, в которых область допустимого изменения каждой переменной – не множество целых неотрицательных чисел, а некоторое заданное конечное множество.

Целочисленные задачи математического программирования могут возникать различными путями.

1. Существуют задачи линейного программирования, которые формально к целочисленным не относятся, но при соответствующих исходных данных всегда обладают целочисленным планом. Примеры таких задач – транспортная задача и ее модификации (задачи о назначениях, о потоках в сетях).

2. Толчком к изучению целочисленных задач в собственном смысле слова явилось рассмотрение задач линейного программирования, в которых переменные представляли физически неделимые величины. Они были названы задачами с неделимостью. Таковы, например, задачи об оптимизации комплекса средств доставки грузов, о нахождении минимального порожнего пробега автомобилей при выполнении заданного плана перевозок, об определении оптимального машинного парка и его оптимального распределения по указанным работам при условии минимизации суммарной стоимости (машинного парка и производимых работ), о нахождении минимального количества судов для осуществления данного графика перевозок и т. п.

3. Другим важным толчком к построению теории целочисленного программирования стал новый подход к некоторым экстремальным комбинаторным  задачам. В них требуется найти экстремум целочисленной линейной функции, заданной на конечном множестве элементов. Такие задачи принято называть задачами с альтернативными переменными. В качестве примеров можно назвать задачи коммивояжера (бродячего торговца), об оптимальном назначении, теории расписания, или календарного планирования, и задачи с дополнительными логическими условиями (например, типа «или – или», «если – то» и т. п.).

---

       Исторически первой задачей целочисленного типа является опубликованная в 1932 г. венгерским математиком Е. Эгервари задача о назначении персонала. В 1955 г. на Втором симпозиуме по линейному программированию была рассмотрена задача о бомбардировщике, известная как задача о ранце.

        Приведем примеры целочисленных задач линейного программирования.

Пример. Задача о ранце. Имеется m-вектор ограниченных ресурсов  , которые можно использовать для перевозки различных по своим характеристикам грузов. Каждый j-й груз   обладает следующими свойствами: 1) неделимостью; 2) полезностью  ; 3) расходом i-го ресурса для перевозки единицы j-го груза    . Выбрать такой номер груза для перевозки, при котором максимизируется общая полезность рейса (суммарная стоимость перевезенных за рейс грузов).

Составим математическую модель задачи. Обозначим через   количество выбранных для траспортировки предметов. Требованию неделимости соответствует условие

целые,                             (13.1)

Сопоставление расходов ресурсов каждого типа для транспортировки единицы груза и их наличия приводит к ограничению

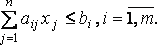                                       (13.2)

Общая полезность рейса определяется значением функции

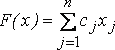.                                       (13.3)

Частным случаем задачи (13.1) – (13.2) является задача о ранце, в которой любой из заданного набора предметов   может быть выбран или нет. Тогда математическая модель примет следующий вид:

Максимизировать

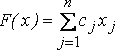
при условиях

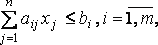
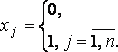
Пример. В области

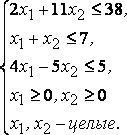
найти максимум функции  .

Решим задачу геометрически (рис. 13.1). Область поиска экстремума – многоугольник OABCD. Так как линия уровня целевой функции параллельна стороне BC многоугольника, экстремум достигается в вершинах   и  , а также в любой точке отрезка BC  и равен 7. Нас интересуют лишь точки с целочисленными координатами, поэтому ни B, ни C не являются допустимым решением задачи. Округлив значение координат точек B и C, получим точку (4; 3), не принадлежащую области поиска. Легко показать, что целочисленный оптимум достигается в точках M(2; 3) и N(3; 2) и равен 5. Обе точки находятся внутри области поиска.

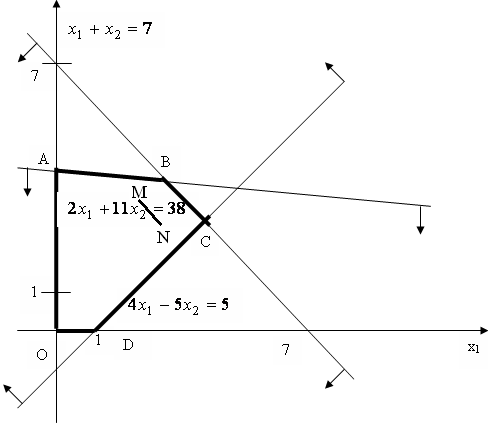
Рисунок 13.1

       Несостоятельность округления подчеркивается также следующими соображениями. Несмотря на то, что целочисленные переменные обычно выражают количество неделимых предметов, возможны и другие типы спецификации этих переменных. Так в задаче о ранце решение представляется булевой переменной   (x = 0 или x = 1). В этом случае бессмысленно оперировать дробными значениями величины x и процедура округления является логически неприемлемой.

        Из приведенного примера видно, что для решения задач целочисленного программирования необходимо рассмотреть особые методы оптимизации. Кроме того, оптимальное решение задач целочисленного программирования не обязательно принадлежит границе многогранника (многоугольника) условий, что характерно для задач линейного программирования.

---

Методы решения задач целочисленного программирования

Методы решения задач целочисленного программирования можно классифицировать как методы отсечения и комбинаторные методы. Дробный алгоритм (в отечественной литературе этот алгоритм называется первым алгоритмом Гомори или циклическим алгоритмом целочисленного программирования); алгоритм, реализующий метод ветвей и границ (предложен А. Лэндом и А. Дойгом с модификацией по схеме Дейкина) подробно изложены в [27 – 35]. Исходной задачей для демонстрации возможностей методов отсечений, используемых при решении линейных целочисленных задач, является задача с ослабленными ограничениями, которая возникает в результате исключения требования целочисленности переменных. По мере введения специальных дополнительных ограничений, учитывающих требование целочисленности, многогранник допустимых решений ослабленной задачи постепенно деформируется до тех пор, пока координаты оптимального решения не станут целочисленными. Название данного метода связано с тем обстоятельством, что вводимые дополнительные ограничения отсекают (исключают) некоторые области многогранника допустимых решений, в которых отсутствуют точки с целочисленными координатами.

      Известно, что при решении задачи линейного программирования в настоящее время принципиальных трудностей нет. Поэтому возникает вопрос: нельзя ли аппарат линейного программирования применять при решении задач целочисленного линейного программирования? Положительный ответ на этот вопрос дает следующая теорема.

    Теорема 13.3. Пусть D – многогранник,   – множество его целых точек,   – выпуклая линейная оболочка множества  . Тогда: 1) R – целочисленный многогранник; 2)  ; 3) множество   опорных планов многогранника R содержится в многограннике  , т.е.  .

Доказательство. Докажем, что R – целочисленный многогранник. По условию теоремы D – многогранник, т.е. ограниченное множество, поэтому   – конечное множество и   – выпуклая линейная оболочка конечного множества точек. Следовательно, R тоже многогранник, причем  , т.е. многогранник R целочисленный. Обозначим его через  . Докажем, что   совпадает с  . Из определения выпуклой линейной оболочки следует, что  .

Покажем, что справедливо также и противоположное неравенство – включение, т.е.  . Пусть  . Поскольку  ,  . Следовательно,  . Но так как произвольный элемент из   принадлежит  , очевидна справедливость того, что  . Из   и   следует, что  .

Включение   очевидно. Поскольку   – множество опорных решений задачи  ,  , но   и поэтому  .

Следствие. Пусть   – оптимальный опорный план задачи (R, F). Тогда   также является оптимальным планом задачи  .

Покажем, что   – единственный целочисленный многогранник, для которого множество его целочисленных точек совпадает с  .

---

     Теорема 13.4. Пусть D – многогранник, L – целочисленный многогранник и

.                                         (13.8)

Тогда  .

Доказательство. Из равенств (13.5) непосредственно следует, что  . Покажем, что  .

Из целочисленности многогранника L имеем, что  . С учетом равенств (13.5) получим  . Отсюда  , т.е.  .

Теорема 13.3 и следствие из нее показывают принципиальную возможность точной линейной аппроксимации целочисленной задачи линейного программирования   с помощью задачи линейного программирования  ; однако они не дают алгоритма для определения  . Кроме того, построение выпуклой линейной оболочки   – не менее сложная задача, и в настоящее время неизвестны эффективные алгоритмы ее решения. В 1954 г. Дж. Данциг, С. Джонсон и Д. Фалкерсон высказали идею о том, что построение   для задачи   можно осуществить поэтапно и решать полученные при этом задачи.

Введем понятие правильного отсечения. Пусть   – некоторая задача целочисленного линейного программирования и опорный оптимальный план   соответствующей задачи линейного программирования (D,  F) не удовлетворяет условию целочисленности

Неравенство

(13.9)

называется правильным отсечением, если оно удовлетворяет условиям:

1) отсечения:   не удовлетворяет неравенству (13.9), т.е.  ;

2) правильности: любое допустимое решение задачи   удовлетворяет неравенству (13.9), т.е.  .

Изложим теперь идею метода.

        1. Задача   решается путем не двухэтапного, а многоэтапного процесса, причем:

         а) на r-м этапе решается вспомогательная задача линейного программирования  ,  . Здесь  ;

         б) множество целых точек – одно и то же для всех многогранников:  .

Следовательно, если оптимальный план   задачи   удовлетворяет условию целочисленности, то он оказывается также и оптимальным планом   исходной задачи  , и процесс решения задачи завершается;

         в) если   не удовлетворяет условию целочисленности, то   не является планом задачи  , т.е.  .

        2. Переход от r-го этапа к (r + 1)-му этапу, т.е. от задачи   к задаче  , в случае нецелочисленности   осуществляется с помощью правильного отсечения  , добавление которого к линейным условиям задачи   превращает многогранник   в многогранник  . Построение дополнительных ограничений и решение возникающей при этом задачи   продолжается до тех пор, пока не получится целочисленное решение или не убедимся в неразрешимости задачи. Однако при этом возникают вопросы: как строить ограничения задачи и обеспечить конечность процесса? Ответ на этот вопрос был впервые получен Р. Гомори, который предложил алгоритм решения полностью и частично целочисленных задач.

 

---

Смотрите также файлы

• 5.5. Методы решения транспортных задач.docx

• 5.4. Некоторые виды задач линейного программирования (транспортная задача, задача о назначениях).docx

• 5.3. Симплекс-метод.docx

• 5.2. Сведения о теоремах линейного программирования.docx

• 5.1. Математическая постановка и методы решения задач линейного программирования.docx