Тема: Целочисленное линейное (дискретное) программирование. Метод ветвей и границ.

Задание: найти решение задачи целочисленного линейного программирования методом ветвей и границ. По плану производства продукции предприятию необходимо изготовить изделия. Составить оптимальный план выпуска продукции, при котором прибыль предприятия от реализации всех изделий была бы максимальной.

Вид сырья	Номы расхода сырья на одно изделие, кг		Общее количество сырья, кг
	Х1	Х2
I II	5 4	7 9	35 36
Прибыль от реализации одного изделия, руб.	2	3

Математическая постановка задачи:

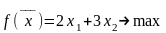
при ограничениях:

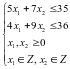
Идея метода ветвей и границ состоит в следующем: множество допустимых решений (планов) некоторым способом разбивается на подмножества, каждое из которых этим же способом снова разбивается на подмножества. Процесс продолжается до тех пор, пока не получено оптимальное целочисленное решение исходной задачи.

Решаем данную задачу как обычную задачу линейного программирования, полагая, что граничное значение функции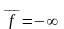 , где - целевая функция. Запишем систему ограничений и целевую функцию:

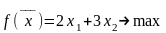
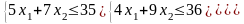
Строим график функции для первого и второго уравнений, для этого выражаем x₂ из 1-го и 2-го уравнений:

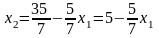- получаем точки (0; 5); (7; 0);

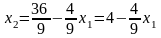- получаем точки (0; 4); (9; 0)

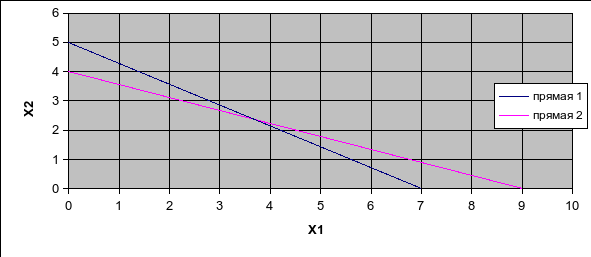
Областью допустимых решений является многоугольник ОАВС, где точки имеют соответствующие координаты: О (0; 0); А (0; 4); В (3,7; 2,35); С (7; 0). Координаты точки В получены в результате пересечений прямых, их находим решая систему уравнений: 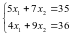. Получаем x₁=3,7 ; x₂=3,7.

Определяем какая из граничных точек многоугольника ОАВС –возможных решений является оптимальной. Для этого можно использовать графический или аналитический симплекс – метод. Симплекс – метод – метод целенаправленного комбинаторного перебора вершин многогранника ограничений результатом которого является выбор оптимальной точки целевой функции. Перебор вершин многогранника ограничений прекращается, если на некотором шаге получена вершина, в которой значение целевой функции хуже, чем в предыдущей.

Точкой, от которой начинается движение вдоль вершин многогранника ограничений является точка О (0; 0), а f(0; 0)=0. Движение будет осуществляться по часовой стрелке.

Найдем значение целевой функции в точке А с координатами (0; 4):

f(0; 4)=2*0+3*4=12. Так как f_A>f_O – движение продолжается.

Найдем значение целевой функции в точке В с координатами (3,7; 2,35):

f (3,7; 2,35)=2*3,7+3*2,35=14,45. Так как f_В>f_А – движение продолжается в том же направлении.

Найдем значение целевой функции в точке С с координатами (7; 0):

f (7; 0)=2*7+3*0=14. Так как f_В>f_С – движение вдоль вершин многогранника прекращается.

Таким образом, получаем что точка В (3,7; 2,35) является оптимальной.

---

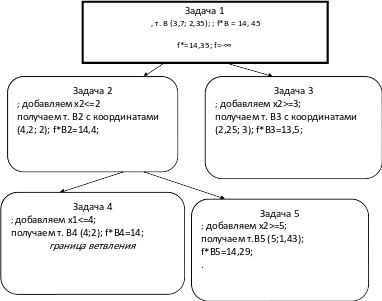
Так как координаты точки В являются нецелочисленными необходимо использовать метод ветвей и границ. Ветвление можно начинать по любой координате (обе они не являются целочисленными). В примере рассмотрено начальное ветвление по второй координате. Задача 1 разбивается на две подзадачи таким образом, что ограничения каждой из полученных задач включают систему ограничений исходной задачи и к ним добавляется для одной подзадачи 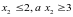- для другой. Целевая функция каждой из полученных подзадач совпадает с целевой функцией исходной задачи.

Рассмотрим продолжение дерева ветвлений к задаче № 3. Окончательные ветви дерева ветвлений для задачи 5 представлены на следующей странице.

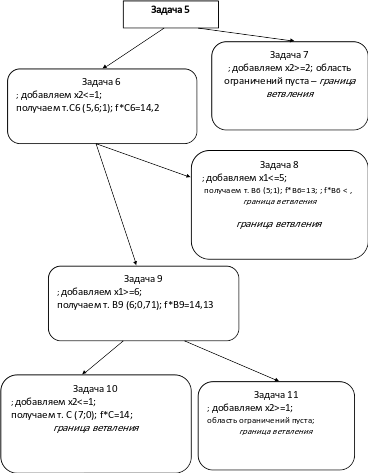
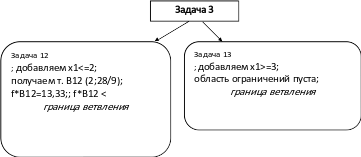
Расположение точек смотреть на рис. 2.

Итак, список задач исчерпан и оптимальным целочисленным решением исходной задачи будет f=14 в точках В(4; 2) и С(7; 0).

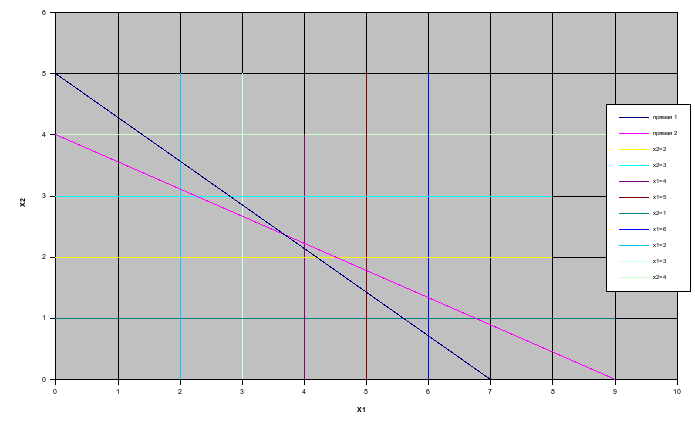Рис. 2. Область допустимых решений

Ответ: оптимальное значение f=14 в точках В(4; 2) и С(7; 0).

---

Смотрите также файлы

• 6.1. Постановка и методы решения задач целочисленного программирования.docx

• 5.5. Методы решения транспортных задач.docx

• 5.4. Некоторые виды задач линейного программирования (транспортная задача, задача о назначениях).docx

• 5.3. Симплекс-метод.docx

• 5.2. Сведения о теоремах линейного программирования.docx