Файл: 9.1. Постановка и методы решения задач стохастического программирования.doc

Таким образом, при нормально распределенных случайных элементах матрицы А и составляющих вектора В решение задачи с построчными вероятностными ограничениями и решение в виде детерминированного вектора сводятся к решению задачи выпуклого программирования с линейной целевой функцией из (10.16) и квадратичными ограничениями из (10.24).

Вариант С. Рассматривается P-модель, у которой требуется минимизация порога k при заданной вероятности ₀ непревышения целевой функцией этого порога.

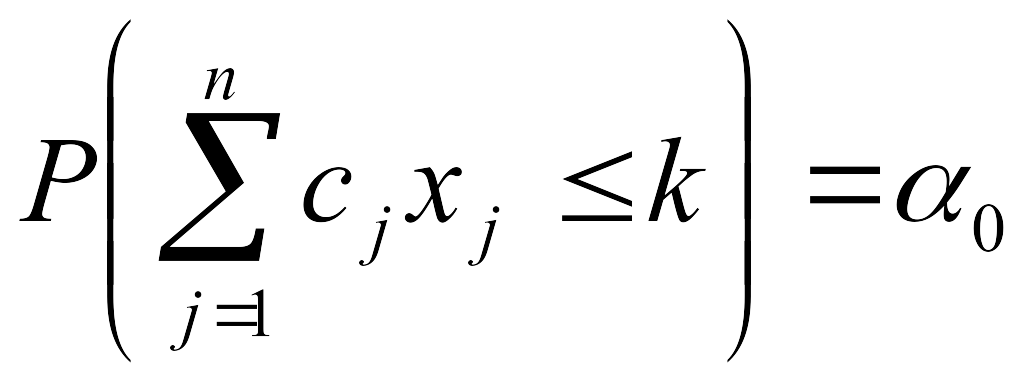. (10.25)

Заданы случайные коэффициенты целевой функции с_j, которые распределены нормально со средним значением и коррелированы между собой.

Корреляция определяется корреляционной матрицей . Целевая функция для нормально распределенной величины с_j будет также нормально распределенной со средним значением и дисперсией .

Среднее значение невязки из соотношения (10.25) . Вводя интеграл вероятности Ф, аналогично (10.23) в принятых обозначениях получим .

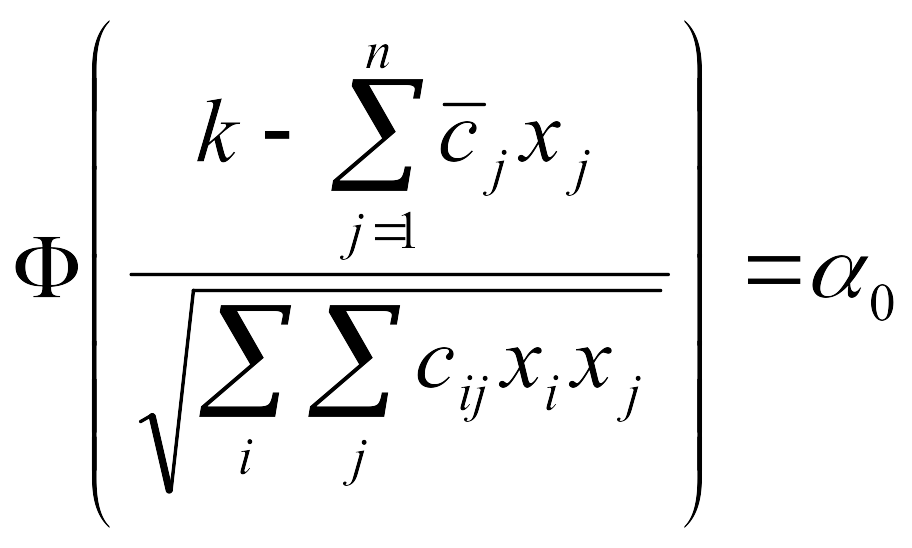Откуда 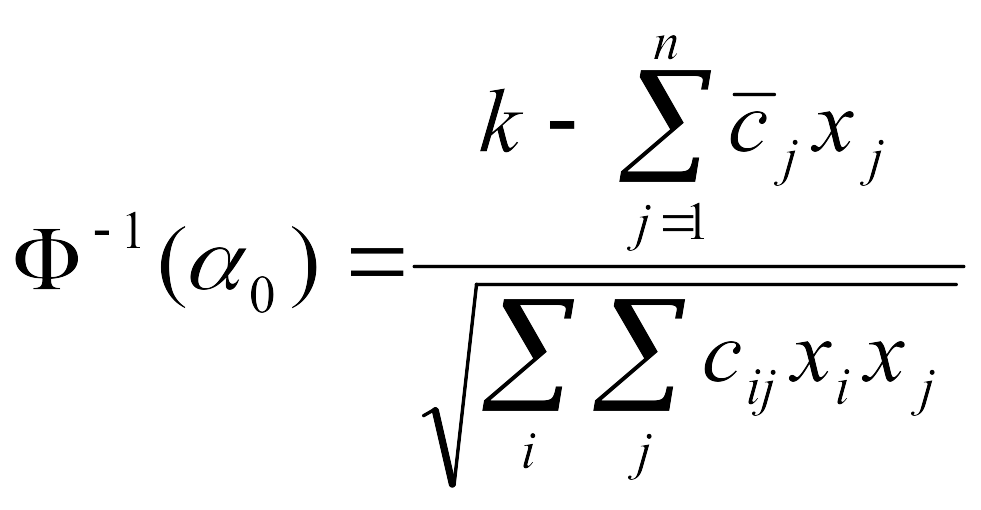. (10.26)

Поэтому целевая функция для минимизации порога k запишется из выражения (10.26) в виде

. (10.27)

Таким образом, при минимизации порога для заданной вероятности непревышения его целевой функцией задача СП с построчными вероятностными ограничениями сводится к детерминированной задаче выпуклого программирования с квадратичной целевой функцией и квадратичными ограничениями.

Например, рассмотрим задачу стохастического программирования, у которой заданы целевая функция в виде Р – модели и построчные вероятностные ограничения в виде

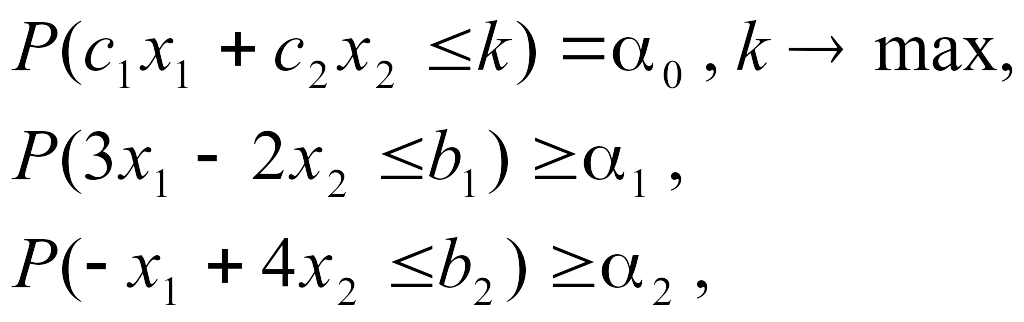
где заданы вероятности ₀=0.37; ₁=₂=0.9.

Матрица системы детерминирована, c₁ ,c₂ ,b₁ ,b₂ – нормально распределенные независимые между собой пары случайных величин со средними значениями , и корреляционными матрицами , .

Можно рассмотреть плотность распределения одной из случайных величин, например b₁ , т. е. , приведенную на рис. 10.3.

По заданному среднему значению строится , смещенная относительно начала координат. Известная величина ₁=0.9 задает площадь под функцией плотности распределения, которая определяет границу =2.72 порога в ограничении, как следует из уравнения (10.17). Из табличных значений обратного интеграла вероятности находится Ф ^–1 (0.37) =0.33.

Таким образом, детерминированный эквивалент рассматриваемой задачи будет иметь целевую функцию

и систему ограничений

Р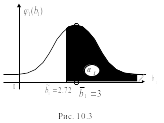
ешение стохастической задачи полностью сводится к решению детерминированной задачи.

10.6. Одноэтапные стохастические задачи с линейными решающими правилами

В рассмотренных ранее задачах решение определялось в виде детерминированного вектора.

Теперь под оптимальным решением подразумевается набор решающих правил, т.е. зависимость компонент решения от реализованных и наблюдавшихся параметров условий задач.

Имеется два типа таких моделей:

1-й тип моделей - функциональный вид решающих правил задается заранее. Характер зависимости решения от реализованных параметров определяется из содержания задачи. Решение стохастической задачи сводится к вычислению детерминированных параметров решающих правил.

2-й тип моделей - функциональный вид решающих правил заранее не определяется, а предполагается заданным функциональное пространство, которому принадлежит решающее правило. Решающие правила представляют собой инструкции, указывающие или конкретизирующие оптимальный план, как только становятся известными реализации случайных исходных данных задачи.

Рассматриваем стохастические модели со следующими условиями:

а) модель имеет построчные вероятностные ограничения;

б) решающие правила представляют собой линейные функции случайных параметров условий задачи;

в) распределение случайных составляющих вектора ограничений и целевой функции подчиняется нормальному закону распределения.

Таким образом, анализируем М-модель с построчными вероятностными ограничениями в виде

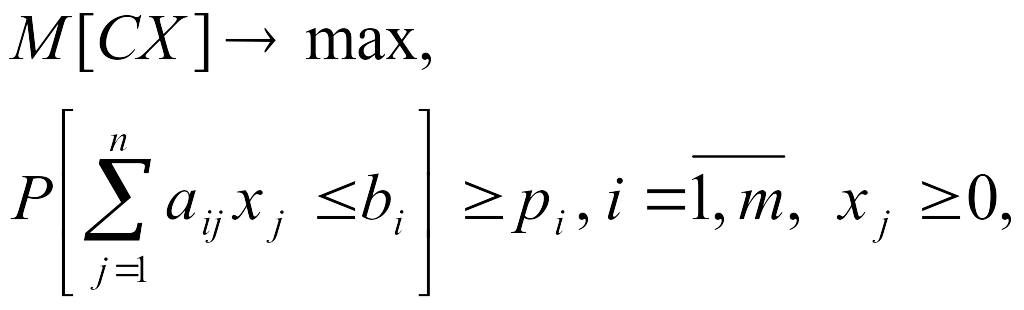(10.28)

где - детерминированная матрица, - независимые случайные векторы, компоненты которых a_ij, b_i и с_j могут быть коррелированы между собой.

Задаем решающее правило в виде X = DB, где [D] =||d_ij|| - неизвестная детерминированная матрица размерностью .

Найти решение задачи означает вычислить элементы матрицы D.

Экономический смысл решающего правила в следующем: в каких пропорциях изменять или выбирать решение Х в зависимости от величины ограничений на ресурсы В.

Вводим элементы определяемой матрицы в целевую функцию, учитывая, что :

(10.29)

где - математическое ожидание векторов С, В.

Теперь изменяем вид ограничений задачи. Обозначим - -ю строку матрицы А, тогда построчное вероятностное ограничение 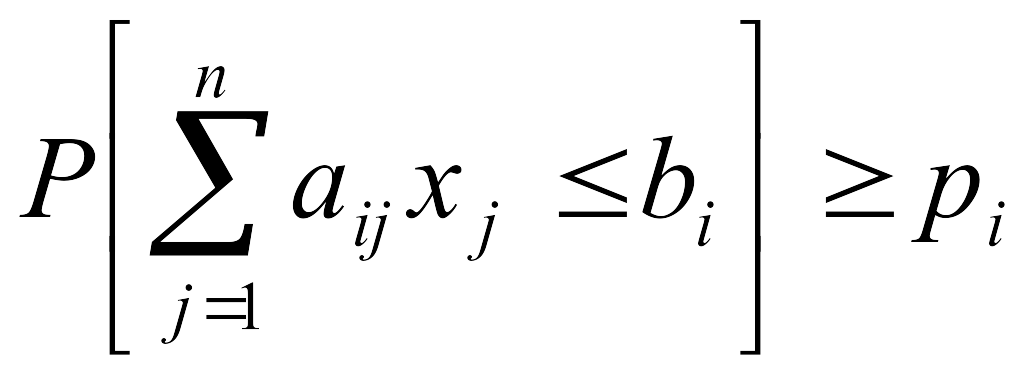можно записать как

(10.30)

Рассмотрим невязку ограничения и обозначим её как S_i , т. е. S_i = b_i - a_iDB, а её среднее значение будет

Вводим вспомогательную случайную переменную в виде

, (10.31)

где _si – среднеквадратическое отклонение невязки:

.

Тогда, подставив значения S_i и , получим

, (10.32)

Её математическое ожидание , т.к. _i – центрированная случайная величина, а дисперсия , т.к. центрированная случайная величина () делится на свое среднеквадратичное отклонение .

Выразим ограничения (10.30) через невязку

(10.33)

а саму невязку – через вспомогательную случайную переменную из выражения (10.31)

.

Невязка в пределе будет равна нулю, если .

Ограничение (10.33) в этом случае будет

,

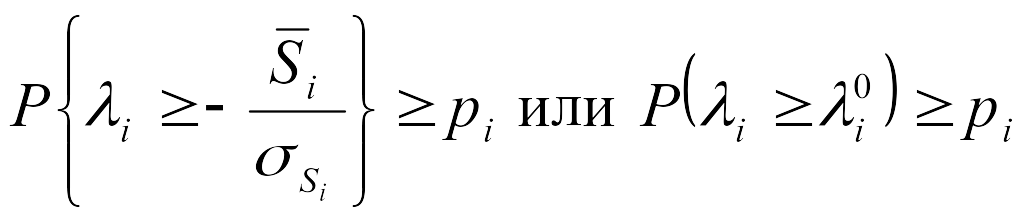где - неслучайная величина, т.к. _si и - неслучайные параметры.

С обратной функцией интеграла вероятности (аналогично варианту В) это ограничение будет ,

где k_i =Ф ^–1 (1 – p_i) – зависит только от вероятности р_i и не зависит от элементов матрицы D. Подставив значения , получим . Вводим вспомогательную переменную так, что

. (10.34)

Это соотношение эквивалентно системе неравенств:

(10.35)

Теперь можно ввести функции, зависящие от искомой величины D:

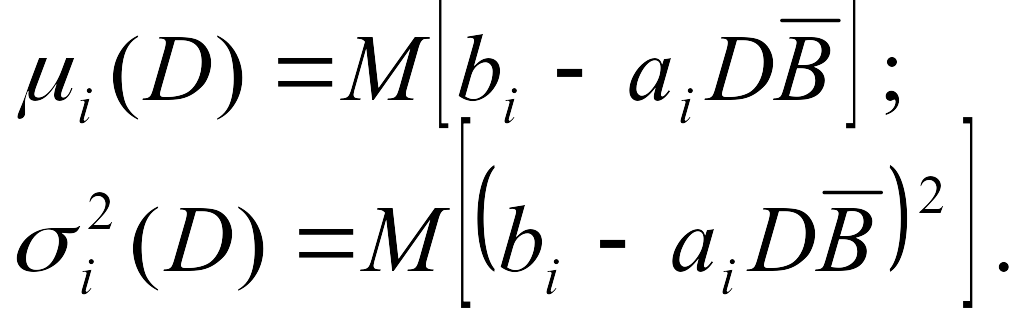
Тогда вся задача может быть записана в виде детерминированного эквивалента относительно искомой переменной D и вспомогательной Z_i:

(10.36)

Таким образом, М-модель стохастического программирования с линейными решающими правилами и построчными вероятностными ограничениями сводится к детерминированной задаче выпуклого программирования с квадратичными ограничениями относительно переменных D и .

10.7. Двухэтапные задачи СП

В практических задачах управления и планирования в условиях риска существуют ситуации, когда целесообразно принять решение в двух формах:

• в виде детерминированного вектора;

• в виде случайного вектора.

Детерминированный вектор определяет предварительное решение, принимаемое до реализации условий задачи.

Случайный вектор соответствует коррекции, вводимой в решение после наблюдения реализованных параметров условий задачи.

Например, можно рассмотреть задачу планирования производства в условиях неопределенного спроса на продукцию. В этой задаче оптимальный план производства содержит две группы параметров:

• первая группа определяет предварительное решение об объеме продукции, что позволяет руководству предприятия подготовить технологию, заключить договора, заказать материалы и начать выпуск продукции;

• вторая группа параметров вычисляется после установления спроса (т.е. наблюдения реализации случайных параметров условий задачи) - это коррекция плана.

Коррекция необходима для компенсации невязок - несоответствия между спросом и объемом выпускаемой продукции, определенными предварительным планом.

Разработка предварительного плана и компенсация невязок - два этапа решения одной задачи. Такие задачи называются двухэтапными задачами стохастического программирования.

В двухэтапных задачах на первом этапе выбирается предварительный план, позволяющий произвести необходимые подготовительные работы. На втором этапе производится компенсация невязок, выявленных после наблюдения реализованных значений случайных параметров.

Целевая функция должна быть такой, чтобы минимизировать среднее значение суммарных затрат, возникающих на обоих этапах.

Рассматриваем задачу, у которой часть элементов матрицы А имеет дополнительные ограничения:

(10.37)

A(w), B(w), C(w) зависят от случайных параметров, т.е. элементы матрицы и векторов являются случайными величинами.

Решение X следует принять до наблюдения реализации случайных параметров. Процесс решения задачи будет следующим.

1. выбирается решение, удовлетворяющее условиям (3), (4).

2. фиксируется реализация случайного события, вычисляются соответствующие ему значения B() и А().

3. оценивается невязка условия (2), т.е.

4. вычисляется вектор Y  0, компенсирующий невязки в соответствии с соотношением 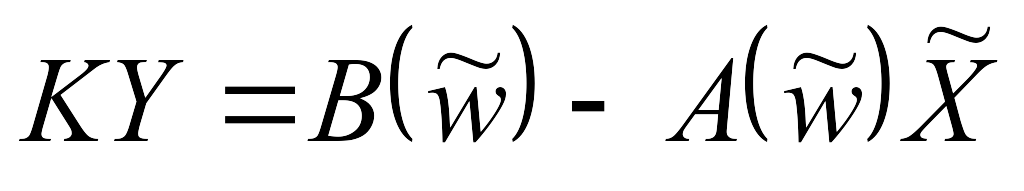, где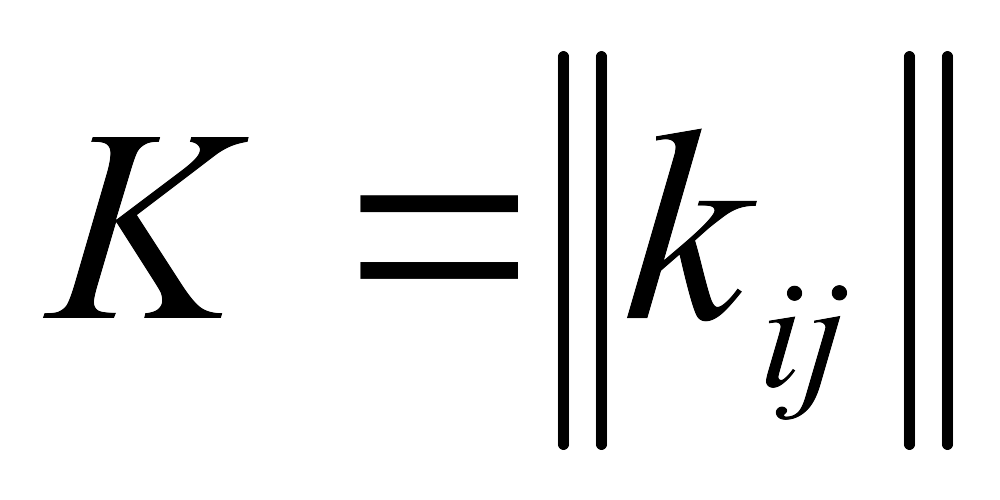 - матрица невязок компенсации.

В общем случае элементы матрицы компенсации К случайны. В производственных терминах: если А - матрица основных технологических способов, то матрица К понимается как матрица аварийных технологических способов, определяющих пути компенсации обнаруженных невязок.

За нарушение условий задачи устанавливается штраф, зависящий от величины составляющих вектора Y с некоторым случайным коэффициентом Q.

Таким образом, вектор Y выбирается так, чтобы обеспечить минимальный штраф за компенсацию невязок условий задачи, определяющихся предварительным планом или решением X.

Следовательно, на втором этапе решается задача:

(10.38)

Оба этапа решения задачи (10.37) и (10.38), сведенные в один, приводят к двухэтапной задаче стохастического программирования:

(10.39)

Таким образом, решение двухэтапной задачи СП состоит из двух векторов:

• детерминированного n-мерного вектора X, определяющего предварительный план;

• случайного п-мерного вектора Y=Y(w), определяющего план компенсации невязок.

Обобщением двухэтапных задач являются многоэтапные задачи СП, у которых на каждом последующем этапе необходимо полностью компенсировать невязки, связанные с принятыми ранее решениями и реализованными параметрами.