Необходимо определить, какая часть выпускаемой продукции в та­ких условиях подвергается контролю и какая часть пропускается на дальнейшие операции без контроля (т.е. какая часть получает отказ от прохождения контрольных операций).

Определим параметр μ потока обслуживания μ = 1/1.25 = 0.8. Отно­сительная пропускная способность q = 0.8 : (1.5 + 0.8) = 0.348. Таким образом, контрольным операциям будет подвергаться менее 35% про­дукции участка. Абсолютная пропускная способность А = 1.5 * 0.348 = 0.52. Вероятность отказа в обслуживании, т.е. пропуска на дальней­шую обработку без контроля, равна (1 - 0.35) = 0.65.

Интересно, что если увеличить производительность труда контро­лера и таким образом снизить продолжительность контрольных опе­раций, то пропускная способность системы, конечно, повысится, однако далеко не до такой степени, как может показаться на первый взгляд. Допустим, что с оснащением контроля новым, более произ­водительным оборудованием s снизилось в 2 раза и соответственно в 2 раза увеличилась интенсивность потока обслуживания, т.е. μ = 1.6. Тогда при той же интенсивности потока заявок получим

q = 1.6/(1.5 + 1.6) = 0.516, т.е. контролироваться будет около 52% всех изделий, а не 70%, как можно было бы ожидать.

Рассмотрим теперь многоканальные системы массового обслуживания.

Для повышения пропускной способности СМО надо увеличить число каналов обслуживания, т.е. число линий связи в телефонной системе, количество контролеров на производстве и т.д. Для потребителя это будет удобно, но общая эффективность системы при этом может сни­зиться, так как каждый новый канал требует дополнительных затрат на установку и обслуживание.

Граф двухканальной системы массового обслуживания с отказами будет иметь вид, показанный на рис. 6.

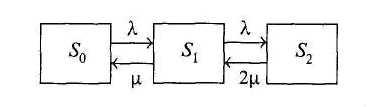
Рис. 6. Граф двухканальной системы массового обслуживания

Состояние S₁ — это состояние, когда в СМО имеется одна заявка и один канал занят, а второй свободен. Из состояния S₀ в состояние S₁ систему переводит поток заявок с интенсивностью λ. Как только при­ходит первая заявка, один канал становится занятым, тот же поток переводит СМО из первого состояния во второе, когда заняты оба канала и следующим заявкам будет даваться отказ.

Если в системе занят один канал, то этот канал производит μ об­служивании в единицу времени. Теперь пусть система находится в со­стоянии S₂, т.е. в ней работают два канала. В состояние S₁ система будет переходить, если обслуживание закончил либо первый, либо второй канал. Таким образом, суммарная интенсивность потока обслужива­ния будет равна 2.

Для состояния S₀ баланс воздействий будет, λ р₀= μ p₁ откуда получим:

Воздействия, выводящие из состояния S₁ (стрелки, направленные из S₁), будут равны λ р₁+ μ p₁. Они компенсируются воздействиями, приводящими в это состояние (стрелки, направленные внутрь S₁):

Баланс воздействий будет равен:

---

С учетом того, что λ р₀= μ p₁ получим: или иначе

.

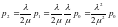Так как сумма всех вероятностей по-прежнему должна равняться единице, получаем:

Откуда следует:

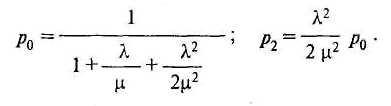
Произведя по полученным формулам соответствующие расчеты из предыдущего примера, получим q = 62%. Таким образом, производи­тельность двух контролеров больше, чем одного, работающего в 2 раза быстрее.

Граф трехканальной системы массового обслуживания с отказами имеет вид, как на рис. 7.

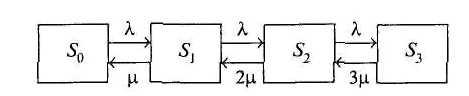
Рис. 7. Граф трехканальной СМО с отказами

Повторяя рассуждения, аналогичные предыдущим, можно получить:

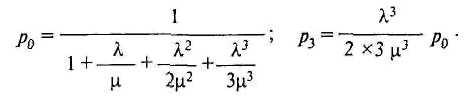
Проделав расчеты с данными для предыдущего примера, в случае трехканальной системы получим q = 81%. Для многоканальных СМО вводится еще один параметр — среднее число занятых каналов

Для системы контроля с тремя контролерами получим k_ср = 1.52. Таким образом, работы не хватает для загрузки даже двух контроле­ров, но все три не обеспечивают 100%-ную проверку всей выпускае­мой продукции. Причина такого положения заключается в случайном характере поступления изделий на контроль.

Можно проверить, что получится, если увеличить число контроле­ров. Хотя, наверное, уже очевидно, что подобный подход явно нельзя назвать эффективным.

На рис. 8 изображен граф n-канальной системы массового обслу­живания с отказами.

Рис. 8. Потоки в многоканальной системе массового обслуживания

Такой же процедурой, которая применялась для 2- и 3-канальных СМО, можно получить:

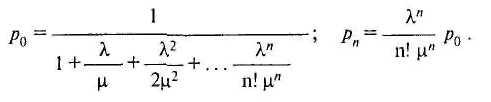
Вероятность отказа равна р_п, а относительная пропускная способность: q =1- Р_n.

В производственной системе с четырьмя контролерами и при тех же интенсивностях потоков, которые указаны в этом примере, получим q = 92%, а среднее число занятых каналов k — 1.75.

Теперь должно быть ясно, что 100% - ной проверки всей продукции таким путем не добиться. Следовательно, необходимо изменить систе­му обслуживания и перейти к СМО с ожиданием.

Системы массового обслуживания СМО с ожиданием

Рассмотрим СМО с одним каналом, на вход которого требования поступают с интенсивностью λ. Заявка, поступившая в момент, когда канал занят, не покидает систему, а становится в очередь и ожидает. Граф состояний такой системы показан на рис. 9.

Рис. 9. Граф системы массового обслуживания с ожиданием

Состояние S₀ соответствует свободному каналу; S₁ означает, что канал занят, но очереди нет; S₂ - канал занят и одна заявка стоит в очереди; S₃ - в очереди две заявки и т.д. В состоянии S_k например, канал занят и (k - 1) заявок ожидают обслуживания. По стрелкам слева направо систему из одного состояния в другое переводит поток заявок с интенсивностью λ, а по стрелкам справа налево переводит поток обслуживании, имеющий интенсивность μ. Всякий раз при переходе из одного состояния в другое очередь изменяется на единицу.

Для получения вероятности начального состояния можно использо­вать уравнение λ р₀ = μ p₁, откуда p₁ = (λ/μ) р₀. Величину λ/μ называют интенсивностью нагрузки СМО. в дальнейшем будем обозначать ее ρ. Для устойчивой работы СМО с ожиданием необходимо, чтобы средняя интенсивность потока обслуживания была больше интенсивности пото­ка заявок, т.е μ > λ и, следовательно, ρ < 1. Если же λ > μ, то система не справится с обслуживанием и очередь будет расти до бесконечности.

---

Используя введенные обозначения, вероятность состояния S₁ мож­но записать в виде: р₁ = ρ р₀. Чтобы получить вероятности р₂ и р₃ можно использовать полученные ранее выражения: p = ρ² р₀ , р₃ = ρ³ p₀. Анало­гично можно получить выражение для произвольного члена: р_k = ρ^k р₀.

Для определения р₀ напишем выражение для суммы вероятностей:

Величина 1 + ρ + ρ² + ... + ρ^k представляет собой сумму членов геометрической прогрессии, она равна 1/(1 - ρ). Поэтому р₀ = 1- ρ, откуда получаем р_к = ρ^k (1 - ρ).

Используя это выражение, можно определить характеристики сис­темы массового обслуживания с ожиданием, существенные для ее функционирования: среднюю длину очереди, среднее число заявок в системе, среднее время пребывания в системе и вероятность образо­вания очереди.

С вероятностью р₂ в очереди стоит одна заявка, с вероятностью р₃ — две заявки и с вероятностью р_k в очереди находится (k — 1) заявок.

Следовательно,

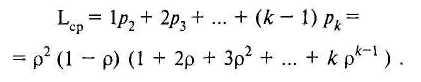
Сумма геометрической прогрессии 1 + 2ρ + 3ρ ² + ... равна 1/(1 - ρ)², поэтому

Среднее число заявок, находящихся в системе обслуживания, со­стоит из среднего числа находящихся в очереди и среднего числа нахо­дящихся на обслуживании, включая интервалы, когда очереди не было. Эта величина ей принимает значение 0, если канал свободен. Вероят­ность такого состояния равна р₀ = 1 - ρ. Если канал занят, значит заявки обслуживаются, и ω принимает значение 1. Вероятность этого равна 1 - р₀= ρ . Следовательно,

Среднее время ожидания в очереди равна среднему числу заявок в очереди, деленному на интенсивность потока обслуживания в одной или в другой форме:

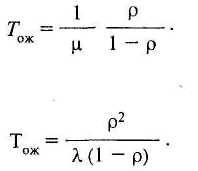
Вероятность образования очереди равна вероятности того, что в системе будет более одного требования, т.е.

Рассмотрим такую же систему контроля продукции, которая была в СМО с отказами, но теперь установим такой порядок, при котором контролер проверяет всю продукцию. Если контролер будет занят, блоки ожидают, пока он освободится. Интенсивность нагрузки в первом случае будет:

При указанных условиях данный режим контроля невозможен, поскольку будет непрерывно возрастать. Во втором случае, т.е после мо­дернизации контрольного оборудования:

В системе будут проверяться все 100% изделий, поэтому прежние параметры (относительная и абсолютная пропускная способность) теперь теряют смысл. Интерес представляет средняя длина очереди, т.е. среднее число изделий, ожидающих, пока контролер освободится и возьмет их на проверку. Для ее определения используем формулу для L_ср = 0.8789/(1 - 0.9375) = 14.06. Среднее число изделий, находящихся в системе, рассчитывается по формуле для ω_ср = =0.9375/0.0625 = 15. Среднее округленное время ожидания в системе контроля определяет­ся по формуле для Т_ож:

Время ожидания находится в допустимых пределах, и систему техни­ческого контроля с ожиданием можно считать вполне приемлемым вари­антом системы технического контроля, обеспечивающей 100%-ную про­верку всех блоков. Вероятность образования очереди при заданных выше интенсивностях потока изделий и производительности контроля р_k= 0,88.

---

Задача № 2.

Фирма организует у себя телефонную связь. Аналитически извест­ны интенсивность потока заявок λ. и интенсивность потока обслужива­нии μ. Необходимо обосновать оптимальное количество каналов обслу­живания. Очевидно, что чем больше количество каналов, тем вероят­ность обслуживания (вероятность связи) выше, но при этом может снизиться эффективность работы станции из-за простоев в этих кана­лах и лишних затрат на обслуживание.

Решение.

Данную задачу можно описать n-канальной системой с отказами.
Граф состояний такой системы показан на рис. 10.

Рис. 10.

Состояния системы:

S_o — все каналы свободны;

S₁ , — занят один канал, остальные свободны;

S₂ — заняты два канала, остальные свободны;

S_n — заняты все п каналов.

Уравнения Колмогорова для такой системы:

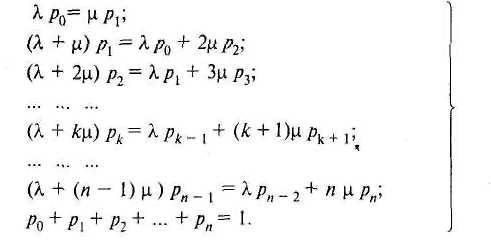
Решая эту систему уравнений, легко можно получить значения р₀, p₁, p₂ и т.д.

Предположим, что на телефонную станцию поступает в среднем 1.5 заявки в минуту, а поток обслуживании имеет интенсивность, рав­ную 0.5 заявки в минуту. Следовательно,

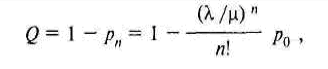
λ / μ = 3. Вероятность обслуживания поступившей заявки для n каналов:

где

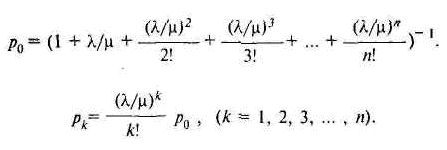
Среднее число занятых каналов:

Для трех каналов (n = 3) получим следующие результаты. Вероят­ность обслуживания заявки Q = 0.65, что составляет 65%. При этом среднее число занятых каналов N = 1.96, что составляет 65% от всех трех каналов. Соответственно 35% поступающих в систему заявок по­лучают отказ.

Увеличим число каналов обслуживания до 4. Получим вероятность обслуживания заявки Q = 0.79, что составляет 79%. Вероятность отказа уменьшается до 21%. Вместе с тем число занятых каналов становится равным 2.38, что составляет 60% от всего числа каналов. Мы видим, что при сравнительно небольшом снижении процента занятых кана­лов (с 65% до 60%) происходит существенное увеличение вероятности обслуживания — с 65 до 79%.

В случае 5 каналов Q — 89%, процент занятых каналов — 53%.

В случае 6 каналов Q = 94%, процент занятых каналов — 47%.

Подведем итоги.

При увеличении каналов с 3 до 4:

• количество занятых каналов снижается на 5 %;

• вероятность обслуживания возрастает на 14 %.
  При увеличении каналов с 4 до 5:

• количество занятых каналов снижается на 7%;

• вероятность обслуживания возрастает на 10%.
  При увеличении каналов с 5 до 6:

• количество занятых каналов снижается на 6%;

• вероятность обслуживания возрастает на 5%.

Таким образом, в динамике мы видим, что увеличение каналов с 3 до 4 является оптимальным, так как при минимальном снижении чис­ла занятых каналов наблюдается максимальный прирост вероятности обслуживания. Дальнейшее увеличение каналов невыгодно из-за про­стоев в них.

Задача № 3.

На автозаправочной станции имеется одна колонка и площадка, на которой могут находится одновременно не более т автомашин. Если все места на площадке заняты, то очередная машина, прибыв­шая к станции, не останавливается, а проезжает мимо. Аналитически было выявлено, что на автозаправочную станцию в среднем в минуту прибывает поток машин с интенсивностью λ₁, а поток обслуживания с интенсивностью μ определяется длительностью заправки.

---

Менеджеров интересуют вероятность отказа в обслуживании и сред­нее время ожидания в очереди в зависимости от мест в очереди т.

Решение.

Данную задачу можно представить в виде одноканальной системы с ограниченной очередью. Число мест в очереди т. Если все места за­няты, то очередная заявка, поступающая в систему, получает отказ. Граф состояний такой системы показан на рис. 11.

Рис. 11

Состояния системы;

S₀, — канал свободен;

S₁ — канат занят, идет обслуживание, но очереди нет;

S₂ — канал занят, одна заявка стоит в очереди;

S₃ — канал занят, в очереди стоят две заявки;

S_m+l — канал занят, в очереди стоят т заявок. Уравнения Колмогорова для такой системы:

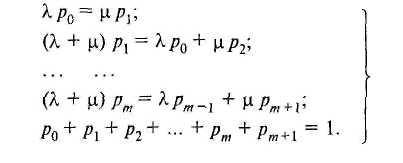
Решая эту систему и вводя = λ/μ, получаем: вероятность свободного канала

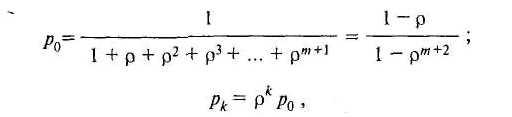
где k = (1, 2, 3, … m+1)

Вероятность отказа p_m+1.

Среднее число заявок в очереди:

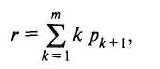
где p_k+1 — вероятность того, что в очереди стоят k заявок.

Среднее время ожидания в очереди: r/λ.

Предположим, что на автозаправочную станцию прибывает в ми­нуту в среднем одна машина. Следовательно, λ = 1.

Предположим, что длительность заправки составляет в среднем 2 мин. Следовательно, μ = 1/2. Таким образом, ρ = λ/μ = 2.

Если число мест в очереди т = 3, то вероятность отказа р_т+1 , = 51,6%, а среднее время ожидания в очереди равно 2,1 мин.

Если число мест в очереди т = 6, то вероятность отказа р_т+1 , = 50,2%. а среднее время ожидания в очереди равно 5 мин.

Видно, что если ρ > 1, то при больших т вероятность отказа стаби­лизируется, становясь равной (ρ — 1 )/ ρ. Чтобы существенно снизить вероятность отказа, необходимо (если нельзя уменьшить ρ) перехо­дить к многоканальным системам.

Задача № 4.

В порту с одним причалом выгружаются прибывающие суда. Аналити­чески известны интенсивность потока заявок λ и интенсивность потока обслуживании (разгрузка судов) μ. При этом может образоваться очередь.

Менеджеров, организующих работу порта, интересуют вероятности очередей размером k и вероятность отсутствия очереди.

Решение.

Данную задачу можно представить в виде одноканальной системы с неограниченной очередью. Граф состояний такой системы показан ниже.

Рис. 12.

Состояния системы:

S₀ — канал свободен (очереди нет);

S₁ — канал занят (идет выгрузка одного судна), но очереди нет;

S₂ — канал занят, в очереди стоит одна заявка;

S₃ — канал занят, в очереди стоят две заявки;

…

S_k — канал занят, в очереди стоят (k — 1) заявок. Эта система характеризуется бесконечным числом дискретных со­стояний.

Вероятность обслуживания без очереди (состояние S₀):

p₀ = 1 - ρ

Вероятность очереди из (k — 1) заявок:

Если условие ρ < 1 не выполняется, то стационарный режим в рас­сматриваемой системе не устанавливается: очередь при t → ∞ растет неограниченно.

Задача № 5.

Имеется инструментальный склад, обслуживающий несколько це­хов фирмы. Аналитически известны интенсивность потока требований на инструмент λ и интенсивность потока обслуживании μ за смену. Известны также потери в единицу времени: от простоя в очереди — п усл. ед., на содержание кладовщика — т усл. ед.

Менеджеров, организующих производственный процесс, интере­сует среднее время ожидания обслуживания и среднее время обслу­живания при разном количестве кладовщиков s инструментального склада. Также важно найти оптимальное количество кладовщиков с учетом затрат в единицу времени на простой в очереди и на содержа­ние кладовщика.

Решение.

При работе одного кладовщика данную задачу можно представить в виде одноканальной системы обслуживания с неограниченной оче­редью:

При ρ > 1 очередь растет неограниченно.

При ρ < 1 имеем следующие показатели.

Вероятность отсутствия очереди:

Вероятность очереди из (k — 1) заявок:

Среднее время ожидания в системе

Среднее время ожидания обслуживания:

Среднее время обслуживания:

При работе s кладовщиков задачу можно описать как многоканаль­ную систему с неограниченной очередью.

Если ρ/s < 1, то существуют финальные вероятности.

Если ρ/s ≥ 1, то очередь растет до бесконечности.

При этом ρ может быть больше 1.

Предположим, что условие (ρ/s) < 1 выполнено. Тогда вероятность

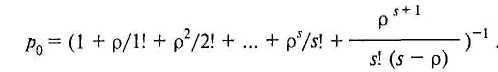
Среднее число заявок в очереди:

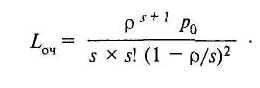
Среднее число заявок в системе (с учетом уже обслуживающихся заявок):

Среднее время пребывания заявки в очереди:

Среднее время пребывания заявки в системе:

Предположим, что затраты в единицу времени на простой состав­ляют 7 усл. ед., а на содержание одного кладовщика 5 усл. ед. Тогда получим следующие результаты при разном количестве кладовщиков (полагаем, что λ = 1.6, μ = 0.9, ρ = =1.77).

При s = 2: Т_с = 5.11, общие затраты 7x 5.11 + 5x2 = 45.77 усл. ед.

При s = 3: Т_с = 1.42, общие затраты 7х 1.42 + 5x3 = 24.94 усл. ед.

При s = 4: Т_с = 1.17, общие затраты 7х 1.17 + 5 х 4 = 28.19 усл. ед.

Видно, что с экономической точки зрения выгодно держать на складе трех кладовщиков.

---

Смотрите также файлы

• 12.2. Классификация систем массового обслуживания.pdf

• 12.1 Теория систем массового обслуживания.docx

• 10.1. Этапы корреляционно-регрессионного анализа.docx

• 9.1. Постановка и методы решения задач стохастического программирования.doc

• 8.2. Примеры решения задач динамического программирования.docx