Файл: 12.2. Классификация систем массового обслуживания.pdf

73

4. ТЕОРИЯ МАССОВОГО ОБСЛУЖИВАНИЯ 

4.1. Классификация систем массового обслуживания и 

их показатели эффективности 

Системы, в которых в случайные моменты времени возникают заявки на 

обслуживание и имеются устройства для обслуживания этих заявок, называ-
ются системами массового обслуживания (СМО). 

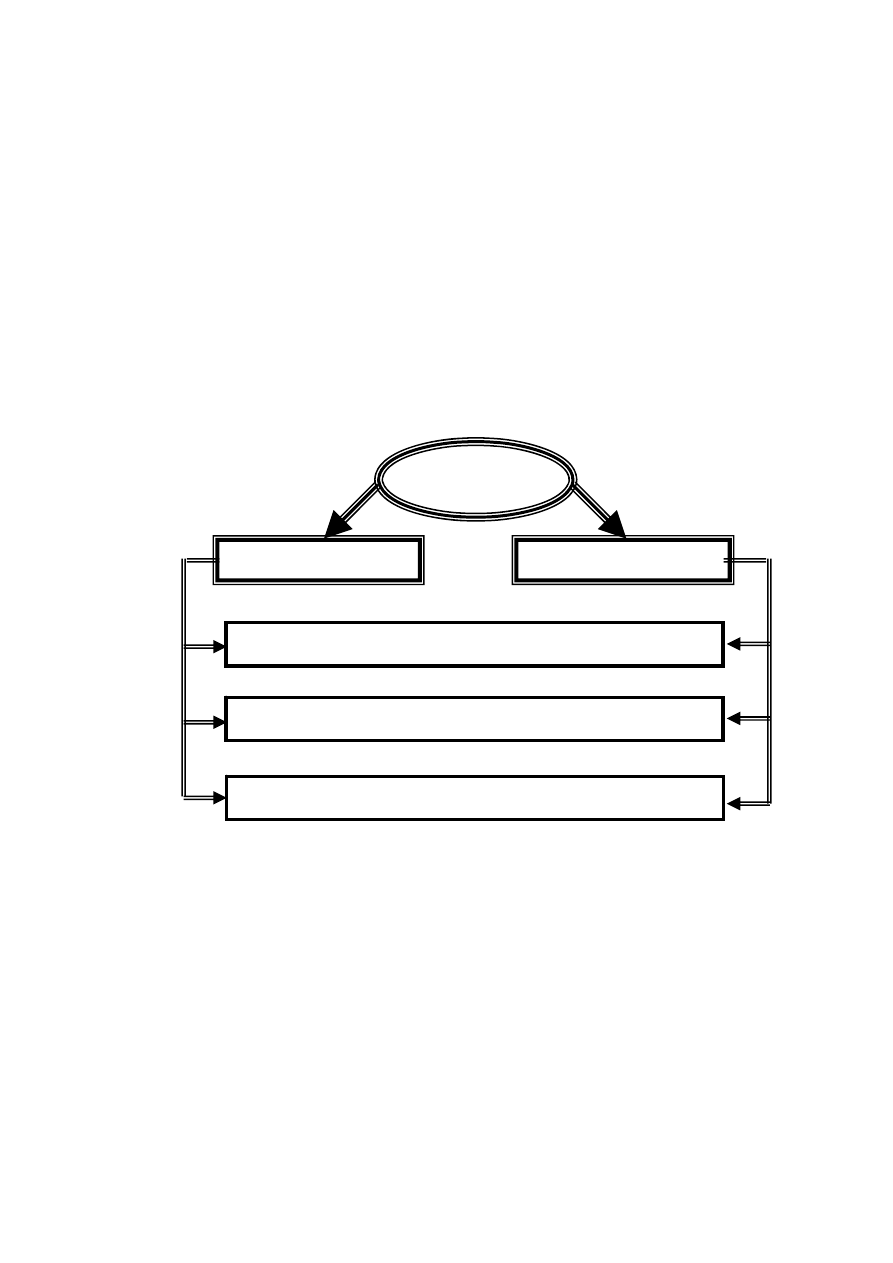
СМО могут быть классифицированы по признаку организации обслужи-

вания следующим образом: 

С М О 

Системы с отказами не имеют очередей. 
Системы с ожиданием имеют очереди. 
Заявка, поступившая в момент, когда все каналы обслуживания заняты: 
-  покидает систему с отказами; 
-  становится  в  очередь  на  обслуживание  в  системах  с  ожиданием  при 

неограниченной очереди или на свободное место при ограниченной очереди; 

-  покидает систему с ожиданием при ограниченной очереди, если в этой 

очереди нет свободного места. 

В  качестве  меры  эффективности  экономической  СМО  рассматривают 

сумму потерь времени:  

-  на ожидание в очереди; 
-  на простои каналов обслуживания. 

многоканальные

с отказами 

с ожиданием при ограниченной очереди 

одноканальные

с ожиданием при неограниченной очереди 

74

Для всех видов СМО используются следующие показатели эффектив-

ности: 

-  относительная  пропускная  способность - это  средняя  доля  посту-

пающих заявок, обслуживаемых системой; 

-  абсолютная пропускная способность - это среднее число заявок, об-

служиваемых системой в единицу времени;  

-  вероятность отказа - это вероятность того, что заявка покинет сис-

тему без обслуживания; 

-  среднее число занятых каналов - для многоканальных СМО. 
Показатели  эффективности  СМО  рассчитываются  по  формулам  из  спе-

циальных  справочников  (таблиц).  Исходными  данными  для  таких  расчетов 
являются результаты моделирования СМО. 

4.2. Моделирование системы массового обслуживания:  

основные параметры, граф состояний 

 
При всем многообразии СМО они имеют общие черты, которые позво-

ляют  унифицировать  их  моделирование  для  нахождения  наиболее  эффек-
тивных вариантов организации таких систем. 

Для моделирования СМО необходимо иметь следующие исходные дан-

ные: 

-  основные параметры; 
-  граф состояний. 
Результатами моделирования СМО являются вероятности ее состояний, 

через которые выражаются все показатели ее эффективности. 

 
Основные параметры для моделирования СМО включают: 
-  характеристики входящего потока заявок на обслуживание; 
-  характеристики механизма обслуживания.   
Рассмотрим характеристики потока заявок. 
Поток  заявок - последовательность  заявок,  поступающих  на  обслужи-

вание. 

Интенсивность потока заявок 

λ  - среднее число заявок, поступающих 

в СМО в единицу времени. 

Потоки заявок бывают простейшими и отличными от простейших. 
Для простейших потоков заявок используются модели СМО. 
Простейшим, или пуассоновским называется поток, являющийся ста-

ционарным, одинарным и в нем отсутствуют последействия. 

Стационарность  означает  неизменность  интенсивности  поступления 

заявок с течением времени. 

75

Одинарным поток заявок является в том случае, когда за малый проме-

жуток  времени  вероятность  поступления  более  чем  одной  заявки  близка  к 
нулю. 

Отсутствие  последействия  заключается  в  том,  что  число  заявок,  по-

ступивших  в  СМО  за  один  интервал  времени,  не  влияет  на  количество  зая-
вок, полученных за другой интервал времени. 

Для отличных от простейших потоков заявок используются имитацион-

ные модели. 

Рассмотрим характеристики механизма обслуживания. 
Механизм обслуживания характеризуется: 
- 

числом n каналов обслуживания; 

-  производительностью канала, или 

интенсивностью обслуживания  μ  

- средним числом заявок, обслуживаемых одним каналом в единицу времени; 

-  дисциплиной  очереди  (например, 

объемом  очереди  m ,  порядком  от-

бора из очереди в механизм обслуживания и т.п.). 

 
Граф состояний описывает функционирование системы обслуживания 

как переходы из одного состояния в другое под действием потока заявок и их 
обслуживания. 

Для построения графа состояний СМО необходимо: 
-  составить перечень всех возможных состояний СМО; 
-  представить  перечисленные  состояния  графически  и  отобразить  воз-

можные переходы между ними стрелками; 

-  взвесить отображенные стрелки, т.е. приписать им числовые значения 

интенсивностей  переходов,  определяемые  интенсивностью  потока  заявок  и 
интенсивностью их обслуживания. 
 
 

4.3. Вычисление вероятностей состояний  

системы массового обслуживания 

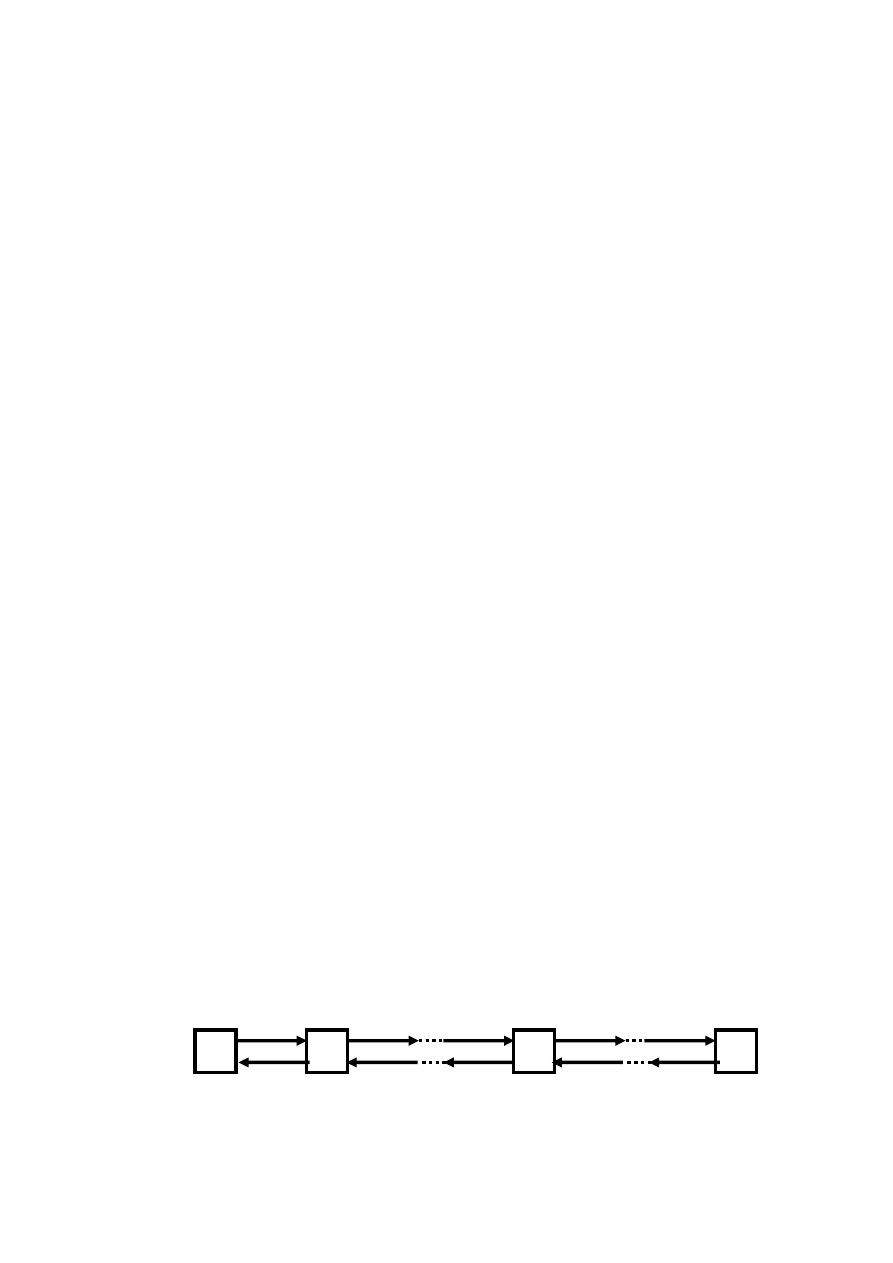
Граф состояний СМО со 

схемой "гибели и рождения" представляет со-

бой  линейную  цепочку,  где  каждое  из  средних  состояний  имеет  прямую  и 
обратную связь с каждым из соседних состояний, а крайние состояния только 
с одним соседним: 

( )

i

1

i

λ

−

1

S

i

S

k

S

1

0

λ

2

1

λ

( )

1

i

i

λ

+

( )

1

i

i

λ

−

( )

i

1

i

λ

+

0

1

λ

1

2

λ

(

)

k

1

k

λ

−

(

)

1

k

k

λ

−

0

S

76

Число состояний

 в графе на единицу больше, чем суммарное число ка-

налов обслуживания и мест в очереди. 

СМО  может  быть  в  любом  из  своих  возможных  состояний,  поэтому 

ожидаемая  интенсивность  выхода  из  какого-либо  состояния  равна  ожидае-
мой интенсивности входа системы в это состояние. Отсюда система уравне-
ний для определения вероятностей состояний при простейших потоках будет 
иметь вид: 

(

)

( )

( )

(

)

( )

( )

(

)(

)

(

)

(

)

(

)(

)

(

)

(

)

(

)

⎪

⎪

⎪

⎪

⎪

⎩

⎪⎪

⎪

⎪

⎪

⎨

⎧

⋅

=

⋅

⋅

+

⋅

=

⋅

+

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

+

⋅

=

⋅

+

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

+

⋅

=

⋅

+

⋅

=

⋅

−

−

−

−

−

−

−

−

−

−

−

+

+

−

−

+

−

;

P

λ

P

λ

,

P

λ

P

λ

P

λ

λ

,

,

P

λ

P

λ

P

λ

λ

,

,

P

λ

P

λ

P

λ

λ

,

P

λ

P

λ

1

k

k

1

k

k

1

k

k

k

1

k

k

2

k

1

k

2

k

1

k

k

1

k

2

k

1

k

1

i

i

1

i

1

i

i

1

i

i

1

i

i

1

i

i

2

1

2

0

1

0

1

2

1

0

1

1

0

1

0

1

0

где 

    -  вероятность  того,  что  система  находится  в  состоянии 

i

P

,

S

i

;

k

,

0

( )

(

i

=

)

(

)

1

i

i

1

i

i

λ

λ

−

+

i

S

 - интенсивность  перехода,  или  среднее  число  переходов 

системы в единицу времени из состояния 

 в состояние 

( )

1

i

1

S

−

∑

=

=

k

0

i

i

1

P

i

P

i

S

+

. 

Используя эту систему уравнений, а также уравнение  

, 

(

вероятность 

  любого 

i

-ого  состояния 

)

k

,

0

i

=

  можно  вычислить  по  сле-

дующему 

общему правилу

: 

вероятность нулевого состояния рассчитывается как  

(

( )

( )

( )

(

)

(

)

( )

)

,

λ

λ

λ

λ

λ

λ

...

λ

λ

λ

λ

λ

...

λ

λ

λ

λ

λ

1

P

1

0

1

1

i

i

1

k

k

k

1

k

i

1

i

1

0

0

1

1

i

i

2

1

1

0

0

1

1

2

2

1

1

0

1

0

0

−

−

−

−

−

−

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

+

+

λ

1

2

i

1

i

−

⋅

λ

λ

2

1

0

1

⋅

λ

1

2

⋅

+ +

⋅

⋅ ⋅ ⋅

⋅ ⋅ ⋅

+

⋅

⋅

+

=

0

P

( )

( )

+

,

S

i

а  затем  берется  дробь,  в  числителе  которой  стоит  произведение  всех  ин-
тенсивностей  потоков  по  стрелкам,  ведущим  слева  направо  от  состояния 

 до состояния 

  а в знаменателе - произведение всех интенсивностей 

по  стрелкам,  идущим  справа  налево  от  состояния 

  до  состояния 

,  и 

эта дробь умножается на рассчитанную вероятность 

0

S

i

S

0

S

(

)

.

P

λ

λ

λ

λ

λ

λ

P

0

0

1

1

2

1

i

i

i

1

i

2

1

1

0

i

⋅

⋅

⋅

⋅

=

−

−

⋅ ⋅ ⋅

⋅

⋅

Выводы по четвертому разделу 

77

Системы  массового  обслуживания  имеют  один  или  несколько  каналов 

обслуживания  и  могут  иметь  ограниченную  или  неограниченную  очередь 
(системы с ожиданием) заявок на обслуживание, не иметь очереди (системы 
с  отказами).  Заявки  на  обслуживание  возникают  в  случайные  моменты  вре-
мени.  Системы  массового  обслуживания  характеризуются  следующими  по-
казателями  эффективности:  относительная  пропускная  способность,  абсо-
лютная пропускная способность, вероятность отказа, среднее число занятых 
каналов. 

Моделирование  систем  массового  обслуживания  осуществляется  для 

нахождения наиболее эффективных вариантов их организации и предполага-
ет  следующие  исходные  данные  для  этого:  основные  параметры,  граф  со-
стояний.  К  таким  данным  относятся  следующие:  интенсивность  потока  зая-
вок, количество каналов обслуживания, интенсивность обслуживания и объ-
ем  очереди.  Число  состояний  в  графе  на  единицу  больше,  чем  сумма  числа 
каналов обслуживания и мест в очереди. 

Вычисление  вероятностей  состояний  системы  массового  обслуживания 

со схемой «гибели и рождения» осуществляется по общему правилу. 

Вопросы для самопроверки 

 
- Какие системы называются системами массового обслуживания? 
- Как классифицируются системы массового обслуживания по признаку 

их организации? 

- Какие системы массового обслуживания называются системами с отка-

зами, а какие – с ожиданием? 

- Что происходит с заявкой, поступившей в момент времени, когда все 

каналы обслуживания заняты? 

- Что рассматривают в качестве меры эффективности экономической 

системы массового обслуживания? 

- Какие используются показатели эффективности системы массового об-

служивания? 

- Что служит исходными данными для расчетов показателей эффектив-

ности систем массового обслуживания? 

- Какие исходные данные необходимы для моделирования систем мас-

сового обслуживания? 

- Через какие результаты моделирования системы массового обслужива-

ния выражают все показатели ее эффективности? 

- Что включают основные параметры для моделирования систем массо-

вого обслуживания? 

- Чем характеризуются потоки заявок на обслуживание? 
- Чем характеризуются механизмы обслуживания? 
- Что описывает граф состояний системы массового обслуживания