Файл: Практикум по измерению электрических и неэлектрических величин.pdf
Добавлен: 28.11.2018
Просмотров: 5330
Скачиваний: 77
21
1.12
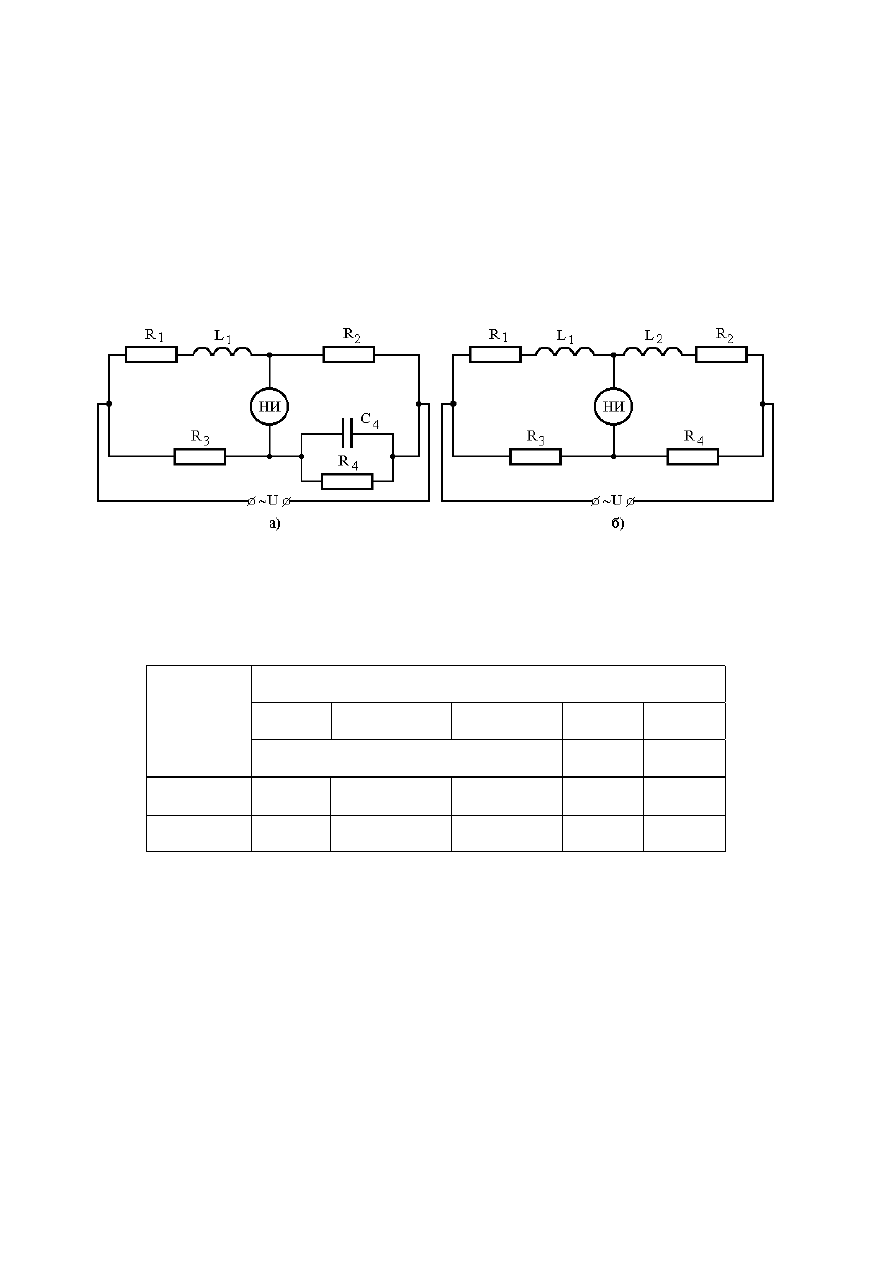
. Мостовые схемы, показанные на рис. 1.11(а, б) и предназначен-
ные для измерения индуктивностей катушек L
1
(их активные сопротивления
R
1
), уравновешены. Запишите условия равновесия и определите индуктивно-
сти катушек L
1
и сопротивления резисторов R
1
для исходных данных, приве-
денных в табл. 1.12.
Рис. 1.11. Мостовые схемы для измерения индуктивностей и активных
сопротивлений катушек
Таблица 1.12
Схема
рис. 1.11
П а р а м е т р
R
2
R
3
R
4
C
4
L
2
Ом
мкФ
мГн
а)
100
10(20 + N) 10(50 – N)
0,5
–
б)
12
10 – 0,2N
20 – 0,5N
–
100
Для выполнения задания необходимо составить уравнения равновесия
моста переменного тока и решить их относительно искомых параметров.
Теория расчёта мостовых схем изложена в литературе по электрическим
измерениям, например в [14–18].
Ответы по 30 вариантам задачи для схемы рис. 1.11(а) приведены в
табл. 1.13. Ответы по этим же вариантам задачи для схемы рис. 1.11(б) даны
в табл. 1.14.

22
Таблица 1.13
N R
1
, Ом L
1
, мГн N R
1
, Ом
L
1
, мГн
N R
1
, Ом
L
1
, мГн
1 42,9 10,5 11 79,5 15,5 21 141,4 20,5
2 45,8 11,0 12 84,2 16,0 22 150,0 21,0
3 48,9 11,5 13 89,2 16,5 23 159,3 21,5
4 52,2 12,0 14 94,6 17,0 24 169,2 22,0
5 55,6 12,5 15 100,0 17,5 25 180,0 22,5
6 59,1 13,0 16 105,9 18,0 26 191,7 23,0
7 62,8 13,5 17 112,1 18,5 27 204,3 23,5
8 66,7 14,0 18 118,8 19,0 28 218,2 24,0
9 70,6 14,5 19 125,8 19,5 29 233,3 24,5
10 75,0 15,0 20 133,0 20,0 30 250,0 25,0
Таблица 1.14
N R
1
, Ом L
1
, мГн N R
1
, Ом
L
1
, мГн N R
1
, Ом
L
1
, мГн
1 6,03 50,3
11 6,46 53,8 21 7,33 61,1
2 6,06 50,5
12 6,51 54,3 22 7,47 62,2
3 6,10 50,8
13 6,58 54,8 23 7,62 63,5
4 6,13 51,1
14 6,65 55,4 24 7,80 65,0
5 6,17 51,4
15 6,72 56,0 25 8,00 66,7
6 6,21 51,8
16 6,80 56,7 26 8,23 68,6
7 6,25 52,1
17 6,89 57,4 27 8,49 70,8
8 6,30 52,5
18 6,98 58,2 28 8,80 73,3
9 6,35 52,9
19 7,09 59,0 29 9,16 76,4
10
6,40 53,3
20 7,20 60,0 30 9,60 80,0
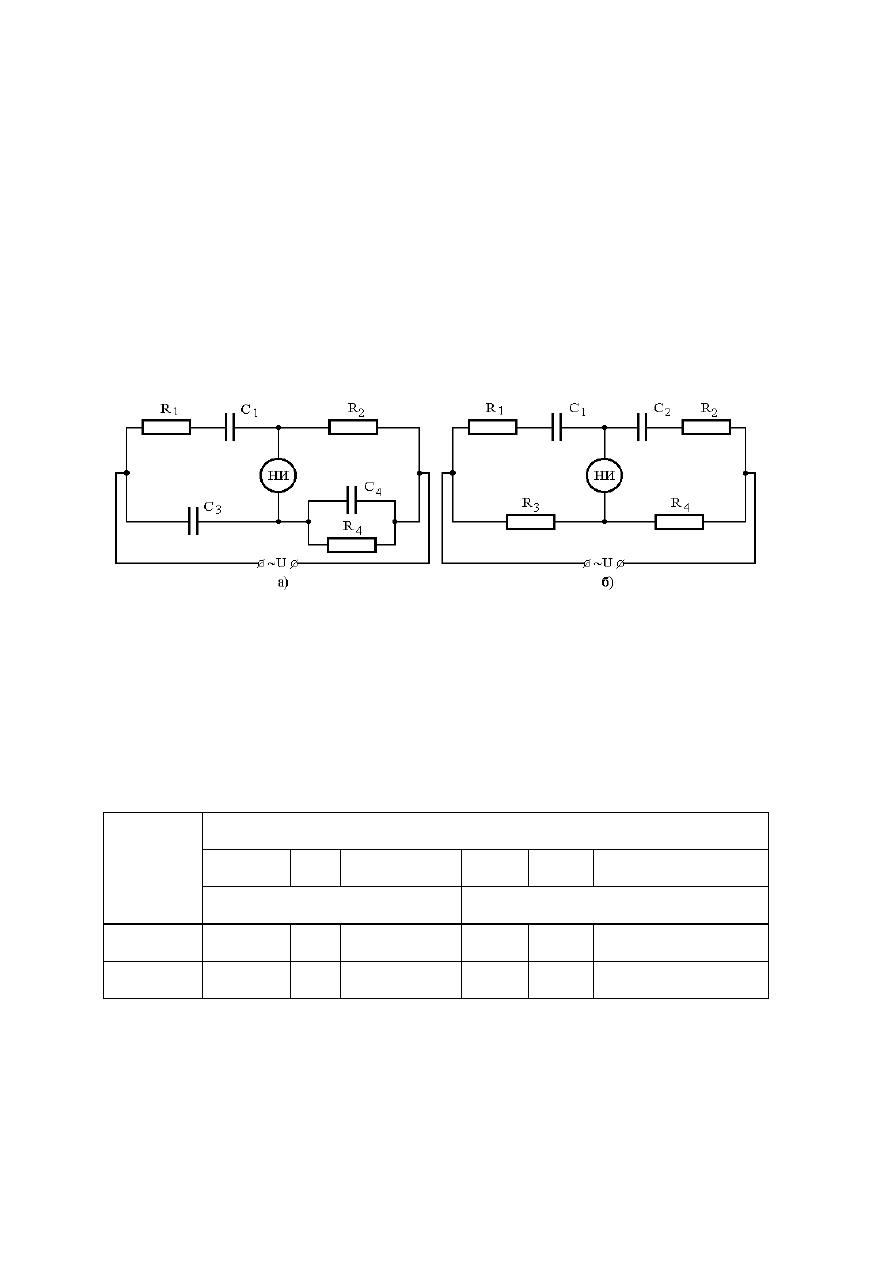
1.13.
Мостовые схемы, показанные на рис. 1.12(а, б) и предназначен-
ные для измерения ёмкостей С
1
конденсаторов с потерями (потери учитыва-
23
ются сопротивлениями R
1
), уравновешены. Запишите условия равновесия и
определите параметры R
1
, C
1
и tg
δ
1
, где
δ
1
– угол диэлектрических потерь
конденсаторов С
1
. Данные, необходимые для расчёта, сведены в табл. 1.15.
Расчёты выполните при условии, что: конденсаторы С
2
, С
3
и С
4
не
имеют потерь; мостовая схема рис. 1.12(а) питается переменным напряжени-
ем с частотой 100 Гц (для чётных вариантов) и 50 Гц (для нечётных вариан-
тов); мостовая схема, показанная на рис. 1.12(б), питается переменным на-
пряжением с частотой 0,5 кГц.
Рис. 1.12. Мостовые схемы для измерения ёмкостей конденсаторов с потерями
Как и при решении предыдущей задачи, из уравнений равновесия мосто-
вой схемы следует выразить неизвестные параметры и рассчитать их чи-
словые значения.
Таблица 1.15
Схема
рис. 1.12
П а р а м е т р
R
2
R
3
R
4
C
2
C
3
C
4
Ом
мкФ
а)
50 + N
–
10(80 + N)
–
0,1
0,01(5 + N)
б)
100 + N 100
200 + 5N
0,05
–
–
Ответы для 30 вариантов задачи по схеме, показанной на рис. 1.12(а),
приведены в табл. 1.16. Ответы к задаче по схеме, показанной на рис. 1.12(б),
даны в табл. 1.17.
24
Таблица 1.16
N
R
1
,
Ом
C
1
,
мкФ
tg
δ
1
10
3
N
R
1
,
Ом
C
1
,
мкФ
tg
δ
1
10
3
1 30,6 1,59
31 16
138,6 1,45
63
2 36,4 1,58
18 17
147,4 1,45 134
3 42,4 1,57
42 18
156,4 1,44
71
4 48,6 1,56
24 19
165,6 1,43
149
5 55,0 1,55
54 20
175,0 1,43
79
6 61,6 1,54
30 21
184,6 1,42
165
7 68,4 1,53
66 22
194,4 1,42
87
8 75,
4 1,52
36 23
204,4 1,41
181
9 82,6 1,51
78 24
214,6 1,41
95
10 90,0 1,50
42 25
225,0 1,40
198
11 97,6 1,49
91 26
235,6 1,39
103
12
105,4 1,48 49 27
246,4 1,39 215
13
113,4 1,48 105
28
257,4 1,38 112
14
121,6 1,47 56 29
268,6 1,38 233
15
130,0 1,46 119
30
280,6 1,38 121
Таблица 1.17
N
R
1
, Ом
C
1
,
мкФ
tg
δ
1
10
3
N
R
1
,
Ом
C
1
,
мкФ
tg
δ
1
10
3
1 49,3 0,103 16,0 16
41,4 0,140 18,2
2 48,6 0,105 16,0 1
7
41,1 0,143 18,5
3 47,9 0,108 16,3 18
40,7 0,145 18,5
4 47,3 0,110 16,4 19
40,3 0,148 18,7
5 46,7 0,113 16,6 20
40,0 0,150 18,9
6 46,1 0,115 16,7 21
39,7 0,153 19,1
7 45,5 0,118 16,9 22
39,4 0,155 19,2
8 45,0 0,120 17,0 23
39,1 0,158 19,4
9 44,5 0,123 17,2 24
38,8 0,160 19,5
10 44,0 0,125 17,3 25
38,5 0,163 19,7
11 43,5 0,128 17,5 26
38,2 0,165 19,8
12 43,1 0,130 17,6 27
37,9 0,168 20,0
13 42,6 0,133 17,8 28
37,7 0,170 20,1

25
14 42,2 0,135 17,9 29
37,4 0,173 20,3
15 41,8 0,138 18,1 30
37,1 0,175 20,4
1.14.
Амперметр класса точности 1,5 со шкалой 0…50 А показал 3N А
(варианты 1–15), а вольтметр класса точности 1,0 со шкалой 0…100 В пока-
зал N В (варианты 16–30). Определите относительную погрешность измере-
ния
δ указанных электрических величин и запишите результат измерения для
каждого прибора.
Зная класс точности прибора и номинальное значение измеряемой ве-
личины (в данном случае – верхний предел измерения), определите допускае-
мую максимальную абсолютную погрешность. Относительная погрешность
измерения находится как отношение абсолютной погрешности к измерен-
ному значению.
Ответы даны в табл. 1.18.
Таблица 1.18
N
δ,%
N
δ,%
N
δ,%
N
δ,%
N
δ,%
1 25,0 7 3,6 13 1,9 19 5,3 25 4,0
2 12,5 8 3,1 14 1,8 20 5,0 26 3,8
3 8,3 9 2,8 15 1,7 21 4,8 27 3,7
4 6,3 10 2,5 16 6,3 22 4,5 28 3,6
5 5,0 11 2,3 17 5,9 23 4,3 29 3,4
6 4,2 12 2,1 18 5,6 24 4,2 30 3,3
1.15.
При поверке электродинамического ваттметра со шкалой
0…500 Вт в одной из её оцифрованных точек получена максимальная абсо-
лютная погрешность 0,2(1+2N) Вт. Определите класс точности и чувстви-
тельность прибора (его шкала имеет 100 делений). Какой будет относитель-
ная погрешность измерения мощности, равной 10N Вт?