Файл: Практикум по измерению электрических и неэлектрических величин.pdf
Добавлен: 28.11.2018
Просмотров: 5334
Скачиваний: 77
31
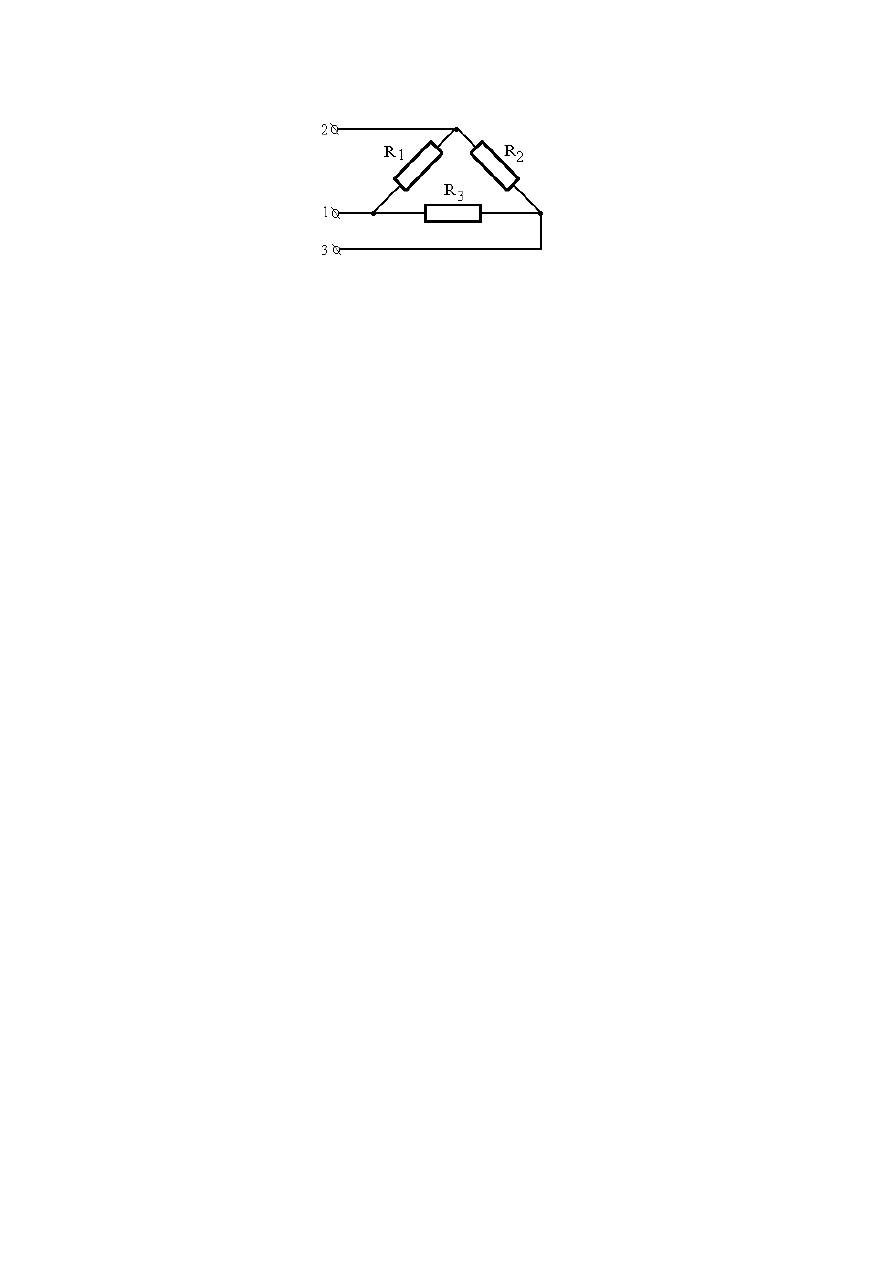
Рис. 1.14. Схема соединения резисторов
Существует несколько путей решения задачи, один из которых – ме-
тод подстановки. Составим систему уравнений:
R
12
=R
1
(R
2
+R
3
)/(R
1
+R
2
+R
3
);
(1.1)
R
23
=R
2
(R
1
+R
3
)/(R
1
+R
2
+R
3
);
(1.2)
R
13
=R
3
(R
1
+R
2
)/(R
1
+R
2
+R
3
).
(1.3)
Вычитая (1.2) из (1.1) и подставляя результат в (1.3), находим
R
2
=К
1
R
1
,
(1.4)
а затем, вычитая (1.3) из (1.1) и подставляя результат в (1.2), находим
R
3
=К
2
R
1
,
(1.5)
где К
1
и К
2
вычисляются по соотношениям:
К
1
=(R
13
–R
12
+R
23
)/(R
13
+R
12
–R
23
);
К
2
=(R
23
–R
12
+R
13
)/(R
23
+R
12
–R
13
).
Подставляя (1.4) и (1.5) в уравнение (1.1), получаем
R
1
=R
12
[1+(К
1
+К
2
)
–1
],
а далее по (1.4) и (1.5) определяем сопротивления R
2
и R
3
.
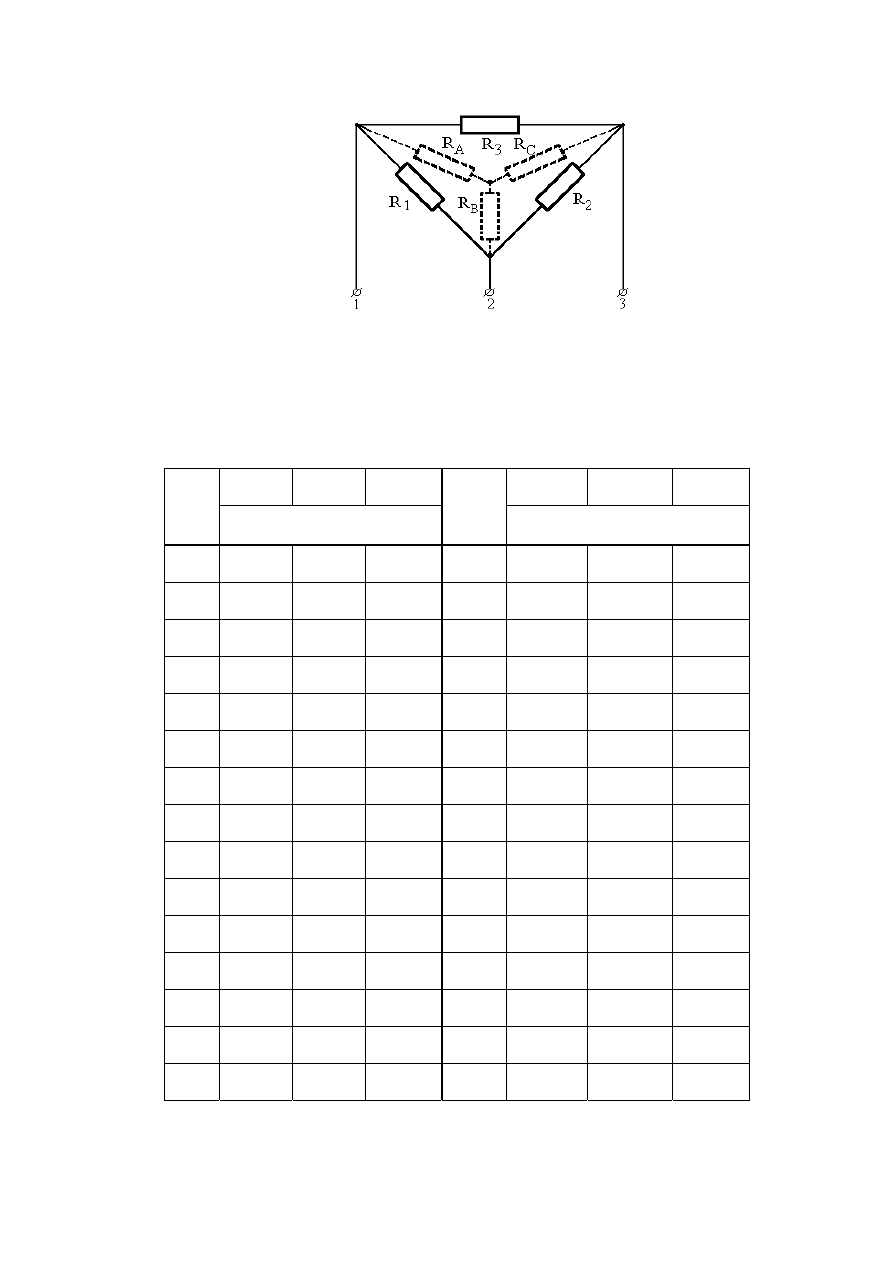
Задачу можно решить и методом эквивалентных преобразований,
заменив «треугольник» «звездой», как показано на рис. 1.15. В этом случае
для определения сопротивлений можно использовать формулы Крамера.
32
Рис. 1.15. Преобразование «треугольника» в эквивалентную «звезду»
Ответы по 30 вариантам задачи сведены в табл. 1.25.
Таблица 1.25
N R
1
R
2
R
3
N R
1
R
2
R
3
Ом
Ом
1 62,80 67,29 104,7 16 80,52 87,16 72,26
2 63.98 68,60 101,5 17 81,69 88,50 70,80
3 65,18 69,92 98,60 18 82,86 89,84 69,38
4 66,36 71,24 95,86 19 84,03 91,18 68,02
5 67,55 72,56 93,29 20 85,19 92,52 66,70
6 68,74 73,88 90,86 21 86,36 93,87 65,42
7 69,92 75,19 88,57 22 87,52 95,22 64,18
8 71,10 76,52 86,39 23 88,68 96,57 62,98
9 72,29 77,85 84,33 24 89,84 97,92 61,80
10 73,47 79,17 82,37 25 91,00 99,27 60,67
11 74,64 80,50 80,50 26 92,15 100,6 59,56
12 75,82 81,83 78,71 27 93,31 102,0 58,47
13 77,00 83,16 77,00 28 94,46 103,4 57,42
14 78,17 84,50 75,36 29 95,61 104,7 56,38
15 79,35 85,83 73,78 30 96,75 106,1 55,37

33
2. ЗАДАЧИ ПО ИЗМЕРЕНИЮ НЕЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
2.1.
При контроле температуры объекта с помощью термоэлектриче-
ского термометра свободные концы преобразователя имели температуру
θ
0
, а
его термо-ЭДС, измеряемая лабораторным потенциометром, оказалась рав-
ной E (табл. 2.1). Определите температуру контролируемого объекта
θ.
Какую термо-ЭДС покажет потенциометр, если температура ОК
уменьшится на 20
°
С, а температура свободных концов ТЭП возрастёт на 8
°
С
относительно соответствующих значений, указанных в табл. 2.1 для каждого
варианта? Определите средние чувствительности (коэффициенты преобразо-
вания) преобразователей ТХК, ТХА, ТПП и ТВР в диапазоне температур
θ
1
…
θ
2
(табл. 2.2).
Таблица 2.1
N
Тип ТЭП
θ
0
,
°
С
E, мВ N Тип ТЭП
θ
0
,
°
С
E, мВ
1
ТХК
15 11,81
13
ТПП
30 13,03
2 20
13,63
14 35
14,13
3 25
16,90
15 40
15,38
4 30
21,89
16 45
15,41
5 35
24,39
17 50
16,13
6 40
28.78
18 55
16,44
7
20 8,66
19
20 4,35
8 25
14,72
20 25
19,75

34
9
ТХА 30 17.35
21
ТВР 30
27,43
10 35
32,24
22 35
30,66
11 40
37,15
23 40
31,19
12 45
41,69
24 45
31,52
Так как по условию задачи термо-ЭДС, измеренная потенциометром,
уменьшена на величину E(
θ
0
, 0), то необходимо найти (например, по табли-
цам [19]) это значение (поправку). Затем определяется термо-ЭДС термо-
метра с учётом поправки E(
θ
, 0)= E(
θ
,
θ
0
)+ E(
θ
0
, 0), а, зная E(
θ
, 0), по тем
же таблицам можно найти температуру
θ
, соответствующую этой тер-
мо-ЭДС. Ответы приведены в табл. 2.3.
Таблица 2.2
N
θ
1
,
°
С
θ
2
,
°
С N
θ
1
, К
θ
2
, К N
θ
1
,
°
F
θ
2
,
°
F N
θ
1
,
°
R
θ
2
,
°
R
1 50 100 7 333 383 13 167 347 19 32 112
2 50 150 8 333 433 14 347 527 20 64 144
3 100 200 9 393 493 15 527 707 21 176 256
4 200 300 10 523 623 16 707 887 22 256 336
5 300 400 11 673 773 17 932 1112 23 336 416
6 400 500 12 773 873 18 1112 1292 24 416 496
Таблица 2.3
N
θ,
°
С
N
θ,
°
С
N
θ,
°
С
N
θ,
°
С
1 178 7 233 13 1304 19 305
2 205 8 384 14 1397 20 1263
3 249 9 451 15 1503 21 1872
4 312 10 809 16 1508 22 2195
5 345 11 936 17 1571 23 2262

35
6 399 12 1058 18 1600 24 2308
Согласно условию задачи далее температура горячего спая преобра-
зователя уменьшилась на
∆θ
и стала равной
θ
–
∆θ
, а температура свобод-
ных концов ТЭП возросла на
∆θ
0
и стала равной
θ
0
+
∆θ
0
. Соответствующие
этим температурам термо-ЭДС находятся по вышеуказанным таблицам
[19]. Показание потенциометра в этом случае будет равно
E(
θ
–
θ
,
θ
0
+
∆θ
0
)=E(
θ
–
∆θ
,0)–E(
θ
0
+
∆θ
0
,0).
Ответы сведены в табл. 2.4.
Средняя чувствительность ТЭП в диапазоне температур
θ
1
…
θ
2
рас-
считывается по формуле:
S=[E(
θ
2
,0)–E(
θ
1
,0)]/(
θ
2
–
θ
1
).
При расчёте S по вариантам 7–24 необходимо учесть, что соотноше-
ния между температурами, выраженными в
о
С, К,
о
F и
о
R, имеют вид:
θ(
о
С)=
θ(К)–273; θ(
о
С)=5[
θ(
о
F)–32]/9;
θ(
о
С)=1,25
θ(
о
R). Ответы приведены в
табл. 2.5.
Таблица 2.4
N E,
мВ N E,
мВ N E,
мВ N E,
мВ
1 9,72 7 7,54 13 12,74 19 3,91
2 11,51 8 13,55 14 13,84 20 19,36
3 14,72 9 16,18 15 15,09 21 26,73
4 19,64 10 31,09 16 15,11 22 29,32
5 22,13 11 36,02 17 15,84 23 30,91
6 26,48 12 40,59 18 16,15 24 31,24
Таблица 2.5
N S
⋅10
2
, мВ/
°
С N S
⋅10
2
, мВ/К N S
⋅10
3
, мВ/
°
F
N
S
⋅10
2
, мВ/
°
R