3. Лабораторная работа № 2
   Решение уравнения вида: F1(x) = F2(x)

Цель работы: получение навыков табуляции функции (нахождение нескольких значений функции для нескольких значений аргумента) и построение диаграмм, графического и точного решения уравнений.

1. Задание

1. Получить 15 значений функций для значений х в диапазоне -2<=х=<2.

2. На графиках найти корни уравнения.

3. Найти точное значение корней, используя инструмент «Поиск решения».

4. Создать лист с лабораторной работой в режиме формул.

2. Методические указания по выполнению работы

Оформить лист в соответствии с представлением в ПРИЛОЖЕНИЕ 3.

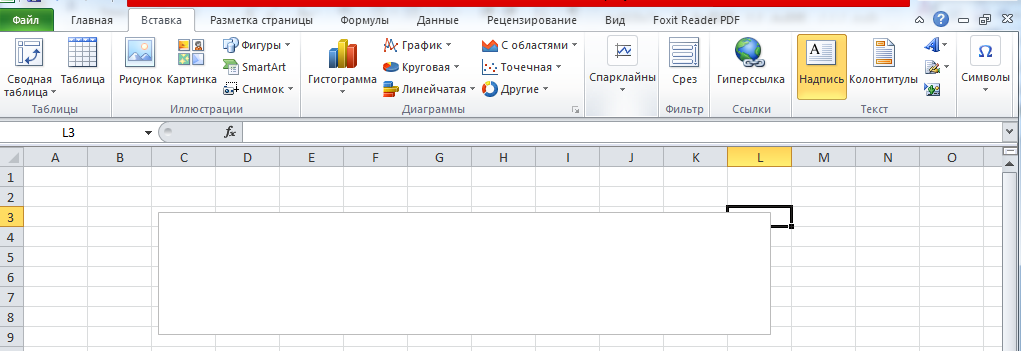
Для вставки текста на лист Excel использовать группу «Вставка» кнопку «Надпись»

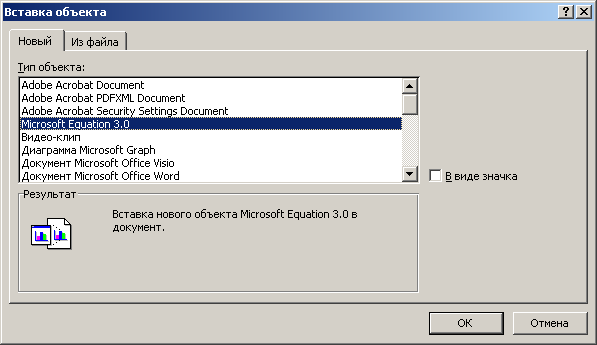
Для вставки формул использовать редактор формул, который находится в группе «Вставка», «Объект». И выбираем редактор формул «Microsoft Equation»

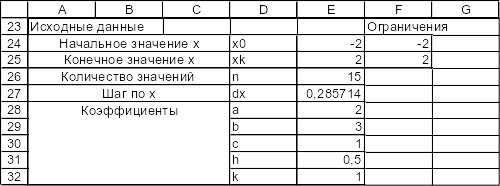
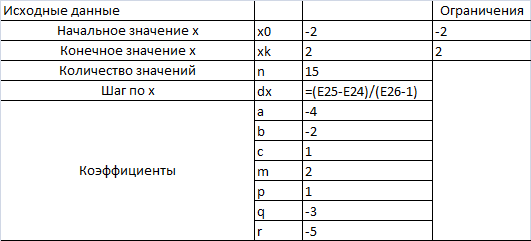
1. Исходные данные.

Решаем уравнение, т.е. находим его корни на отрезке от х0 до хк, всего значений берём n =15, с шагом dx. Исходные данные x0, xk, n, dx - для всех вариантов одинаковы, вид уравнения и коэффициенты а,b,с, h, k ...– берутся из ПРИЛОЖЕНИЯ 2, в соответствии с вариантом задания. Величина шага рассчитывается по формуле: dx=(xk‑x0)/(n-1). В Excel в формулах используются не значения, а адреса ячеек в которых хранятся эти значения. Поэтому, для расчета величины шага в EXCEL в ячейку «E27» (величины коэффициентов и адреса ячеек соответствуют только данному примеру) вместо числового значения подставляется формула: =(Е25‑E24)/(Е26-1).

Исходные данные представляются в отдельной таблице:

2. Графическое решение уравнений

Решением уравнения будут значения «x», при которых графики левой и правой части уравнения пересекаются друг с другом.

Для графического решения уравнения

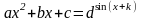
представим левую и правую части уравнения в виде отдельных функций

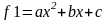
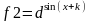
и будем искать решение уравнения

.

В этом случае решением уравнения будут точки пересечения графика функции F с осью «X».

Для построения графика функции в EXCEL функция представляется в табличном виде, т.е. табулируется. Табуляция выполняется в следующей последовательности:

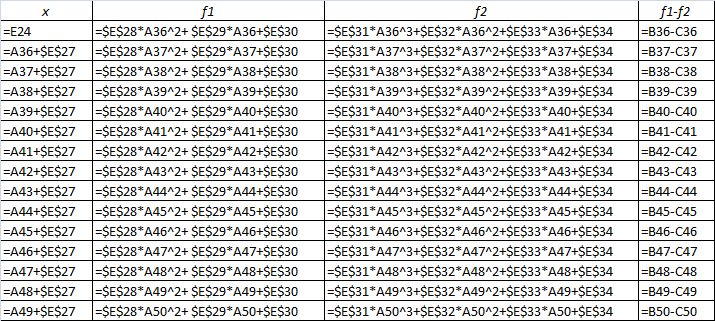
1. Рассчитать значения «х». Первым значение «х» является нижний предел диапазона значений (ячейка «А36»). Вторым значение «х» будет сумма первого значения «х» и шага по «х» (ячейка «А37»). Ссылка на ячейку «А36» - относительная, на ячейку «Е27» - абсолютная. Ячейка «А35» - имя столбца.

Остальные значения «х» получаются путем распространения формулы в ячейке «А37» на нижерасположенные ячейки до значения «xk». Курсор устанавливаем на правый нижний угол ячейки с формулой, нажимаем левую кнопку мыши, курсор принимает вид «+» и не отпуская левую кнопку мыши, растягиваем формулу до тех пор, пока не получим значение конечного х = 2.

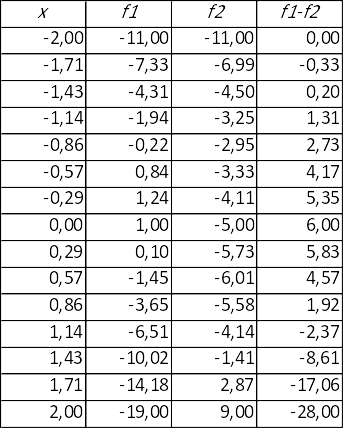
2. Рассчитать значения функции f1, f2 и f1-f2 для полученных значений «х». Расчеты производятся в столбцах «B», «C» и «D».

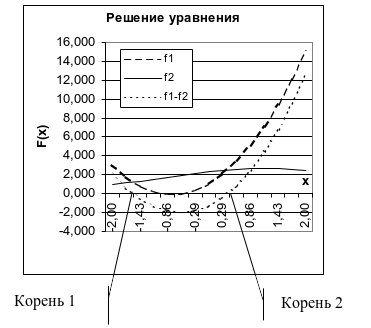
По таблице табуляции построить графики функций f1, f2, f1-f2 (Error: Reference source not found) и по ним найти графическое решения уравнения.

Режим значений

A B C D

Режим формул

B D E F

A B C D

ПРИМЕЧАНИЕ. В примере функция f1 – квадратичная, f2 – кубическая. Математическая функция 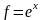в EXCEL имеет вид =EXP(x).

3. Точное решение уравнения. Сервис «Поиск решения».
   
   
   

Не всегда по графику удаётся определить точное решение уравнения. Напоминаю, что мы ищем те значения аргумента «x», при которых разность f1(x)-f2(x) принимает значение равное «0». Проанализируем полученный столбец этих значений в Excel и увидим, что есть только близкие к нулю значения. Наша задача найти точное решение. Для этого продолжая анализировать полученные результаты в столбце «f1-f2», замечаем, что есть интервалы, в которых значения меняют знак с плюса на минус или наоборот (см. выше таблицу «Режим значений»). Очевидно, что именно на этом интервале находится нулевое значение, для его нахождения можно разбить этот интервал на более мелкие интервалы и определить при каких же значениях «х», разность f1(x)-f2(x)=0. Для этого будем использовать сервис «Поиск решения».

Для точного решения уравнения используется инструмент «Поиск решения». «Поиск решения» в Microsoft Office 2010 можно разместить на ленте через группу «Файл» –> «Настройка ленты» – > «Разработчик».

Для Microsoft Office 2007 кнопка «Office» –> «Параметры Excel» –> «Надстройки» –> устанавливаем курсор на «Поиск решения» –> «Перейти». Устанавливаем галочку напротив «Поиск решения» – «OK»

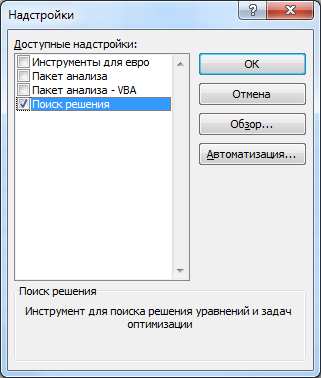
• «Поиск решения» размещается на ленте в группе «Данные»
  
  
  
  

• В окне «Поиск решения» выполнить следующие установки:

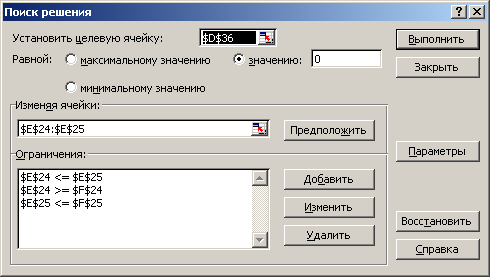
1. «Установить целевую ячейку» - это адрес ячейки верхней границы интервала, в столбце значений функции «f1(x)-f2(x)», в котором значение функции меняет свой знак с плюса на минус либо наоборот, именно на этом интервале функция принимает значение равным «0». Наша задача определить это значение аргумента, которое и будет являться корнем уравнения.

2. Настройка «Равной» - указывается значение, которое должно быть в целевой ячейке. В нашем случае устанавливается «значение» и величина целевой ячейки равняется «0».

3. «Изменяя ячейки» - это диапазон адресов ячеек, внутри которого будет подбираться значение, чтобы целевая функция приняла требуемое значение. В нашем случае это адреса ячеек с начальным и конечным значением «х» («х0» и «хk»).

4. «Ограничения» - устанавливаются требуемые ограничения на значения переменной. Для решения уравнения эти ограничения будут:

x0>=ограничение снизу;

x0<=xk;

x0<=ограничение сверху;

xk<=ограничение сверху.

Для установки ограничений надо нажать кнопку «Добавить».

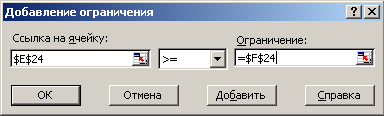
5. После выполнения всех установок нажать кнопку «Выполнить». Если уравнение имеет решение, появится сообщение:

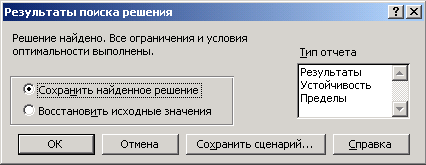
6. После нажатия кнопки «ОК» в целевой ячейке будет значение =0, а ячейке «х» - корень уравнения.

Поместить копию строки с найденным решение под таблицей, выполнив сначала команду «Копировать», а затем «ПравкаСпециальная вставка значения».

Остальные корни находятся аналогично с другой целевой ячейкой.

2. Лабораторная работа № 2
   Аппроксимация функции линиями тренда.

Цель работы: приобретение навыков использования имен ячеек, аппроксимации функции линиями тренда и построение прогноза.

1. Задание

1. Присвоить ячейкам с исходными данными имена

2. Построить таблицу функции f(x) для 15 значений х в диапазоне -2<=х=<2.

3. Построить график исходной функции, выполнить аппроксимацию линиями тренда двух типов.

4. С помощью линий тренда построить прогноз на 2 периода вперед.

5. Создать лист с лабораторной работой в режиме формул.

2. Методические указания по выполнению работы

Сделать копию листа с первой лабораторной работы (Error: Reference source not found) и переименовать его. Доработать лист в соответствии с ПРИЛОЖЕНИЕ 3.

1. Присвоение имен ячейкам

Присвоение имен ячейкам позволяет использовать в формулах не ссылки (адреса), а имена ячеек. В этом случае имена ячеек являются абсолютными ссылками. В конкретном случае это исходные данные: x0, xk, n…

1. Выделить ячейки с исходными данными и обозначениями этих данных.

2. Выбрать группу «Формулы» вкладку «Создать из выделенного». Ячейкам правого столбца будут присвоены имена, которые стоят в левом столбце.

3. Чтобы поместить на лист имена ячеек и их адреса надо поставить курсор на свободное место и выбрать группу «Формулы» вкладку «Использовать в формуле» «Вставить имена», в открывшемся окне нажать кнопку «Все имена»;

4. Для применения имен ячеек в формулах надо выбрать группу «Формулы» «Вставка» «Присвоить имя» «Применить имена»; в открывшемся окне выделить все имена (если они не выделены) и нажать кнопку «ОК».

2. Построение линий тренда

Линии тренда позволяют проводить регрессионный анализ, т.е. продлить линию тренда в диаграмме за пределы реальных данных для построения прогноза.

Линия тренда строится для одной из функций предыдущей работы.

Построение линии тренда.

1. Выделить график.

2. Выбрать группу «Макет» кнопка «Линия тренда» «Дополнительные параметры линии тренда»

3. В открывшемся окне выбрать тип линии тренда

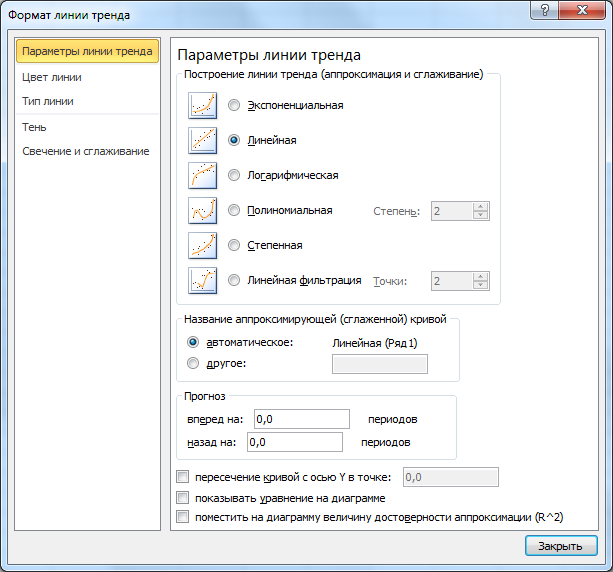
4. Установить число периодов прогноза и поставить флажок в строке «Показывать уравнения на диаграмме».

3. Лабораторная работа № 3
   Аппроксимация функции

Цель работы: - получение навыков аппроксимация функции линейной и логарифмической функциями, использование мастера функций.

1. Задание

1. Найти коэффициенты аппроксимирующих функций, используя мастер функций.

2. Протабулировать аппроксимирующие функции в тех же пределах х, что и исходная функция.

3. Найти отклонения между функцией и аппроксимирующей функциями.

4. Найти среднее отклонение и дисперсию отклонения.

5. Построить графики функции и аппроксимирующих функций.

6. Создать лист с лабораторной работой в режиме формул.

2. Методические указания по выполнению работы

Сделать копию листа со второй лабораторной работой (Error: Reference source not found) и оформить ее в соответствии с ПРИЛОЖЕНИЕ 3.