Добавлен: 28.11.2018
Просмотров: 3562
Скачиваний: 53

В соответствии с учебным графиком для студентов, обучающихся
по направлению 15.03.04 «Автоматизация технологических процессов
и производств», предусмотрено выполнение одного индивидуального
домашнего задания (ИДЗ), которое заключается в решении всех задач
по четырем указанным темам. Выполнение этого ИДЗ необходимо
для закрепления теоретических знаний и приобретения практических
навыков вычислений надёжности системы и её резервирования.
Курс «Диагностика и надёжность автоматизированных систем» яв-
ляется основным в теоретической подготовке бакалавра по направле-
нию 15.03.04 «Автоматизация технологических процессов и произ-
водств». Элементы данного курса применяются при выполнении вы-
пускной квалификационной работы. Отсюда следует требование к серь-
езному усвоению и осмыслению основных положений данного курса.
Требования к оформлению ИДЗ
При оформлении индивидуального домашнего задания необходимо
соблюдать следующие требования:
1. Индивидуальное задание должно иметь титульный лист, оформ-
ленный в соответствии со стандартами ТПУ. На титульном листе ука-
зываются номер индивидуального задания, номер варианта, название
дисциплины; фамилия, имя, отчество студента; номер группы, шифр.
2. Текст индивидуального задания набирается в текстовом процес-
соре Microsoft Word. Шрифт –Times New Roman, размер – 12–14 pt, для
набора формул рекомендуется использовать редактор формул Microsoft
Equation или MathType.
3. Решения задач следует располагать в той же последовательно-
сти, что и задания.
4. Каждая задача должна начинаться с условия задачи, ниже крат-
кая запись задачи, если необходимо – рисунок с условными обозначе-
ниями, которые в дальнейшем будут использованы при решении задач.
5. Решение должно быть подробным, с включением промежуточ-
ных расчётов и указанием использованных формул.

2
Варианты ИДЗ и методические указания
Для решения задач ИДЗ необходимо воспользоваться учебным по-
собием:
Шкляр В.Н. Надежность систем управления: учебное пособие /
В.Н. Шкляр; Томский политехнический университет. – Томск: Изд-во
Томского политехнического университета, 2011. – 126 с.
Тема 1. Расчет надёжности систем [1, с. 17–34].
Тема 2. Обеспечение заданного уровня надёжности технических
систем [1, с. 35–54, 60–61].
Тема 3. Основные вопросы эксплуатационной надёжности тех-
нических систем [1, с. 89–103].
Тема 4. Диагностика автоматизированных систем [1, с. 55–85].
Номер варианта ИДЗ определяется по последней цифре номера
зачетной книжки. Например, если номер зачетной книжки Д-11Г10/12,
то номер варианта задания равен 2. Если номер зачетной книжки оканчи-
вается на 0 (например, З-3Б10/30), то номер варианта задания равен 10.

3
Вариант 1
Тема 1. Расчет надёжности систем
1. Интенсивность отказов автоматизированной системы определя-
ется зависимостью
t
b t
ч
–1
. Определите частоту отказов a(t) авто-
матизированной системы.
2. Интенсивность отказов системы
t
b
t
ч
–1
, b = 10
–6
ч
–2
. Опреде-
лите вероятность безотказной работы системы P(t
1
, t
2
) в течение нара-
ботки от t
1
до t
2
, если t
1
= 1000 ч, t
2
= 2000 ч.
3. По результатам испытания 300 приводов исполнительных меха-
низмов, проводившихся без замен и отказавших в течение 1 000 часов,
были получены данные о наработках до отказа, приведённые в табл. 1.1.
Таблица 1.1
Интервалы наработки
, ч
i
t
0–100 100–200 200–400 400–600 600–800 800–1000
Число отказов
i
n t
70
90
60
35
25
20
Вычислить значения и построить графики вероятности безотказной
работы, интенсивности отказов, частоты отказов приводов исполни-
тельных механизмов.
4. На насосной станции магистрального трубопровода установле-
ны 3 насоса, наработка до отказа которых определяется нормальным за-
коном распределения с параметрами:
насос 1: m
1
= 2800 ч, σ
1
= 1600 ч;
насос 2: m
2
= 3200 ч, σ
2
= 1000 ч;
насос 3: m
3
= 4200 ч, σ
3
= 2000 ч.
Время безотказной работы системы управления насосами опреде-
ляется законом Рэлея с параметром λ
С
= 0,0002 ч
–1
. Определите, какова
будет вероятность безотказной работы манипулятора через неделю не-
прерывной работы в три смены?
5. Установлено, что наработка до отказа привода задвижки имеет
распределение Вейбулла с параметром
8
,
1
. Вероятность безотказной
работы привода в течение наработки (0, 100) часов равна 0,95. Требует-
ся определить интенсивность отказов в момент времени t = 100 ч,
и среднюю наработку до отказа привода.
4
Тема 2. Обеспечение заданного уровня надёжности технических
систем
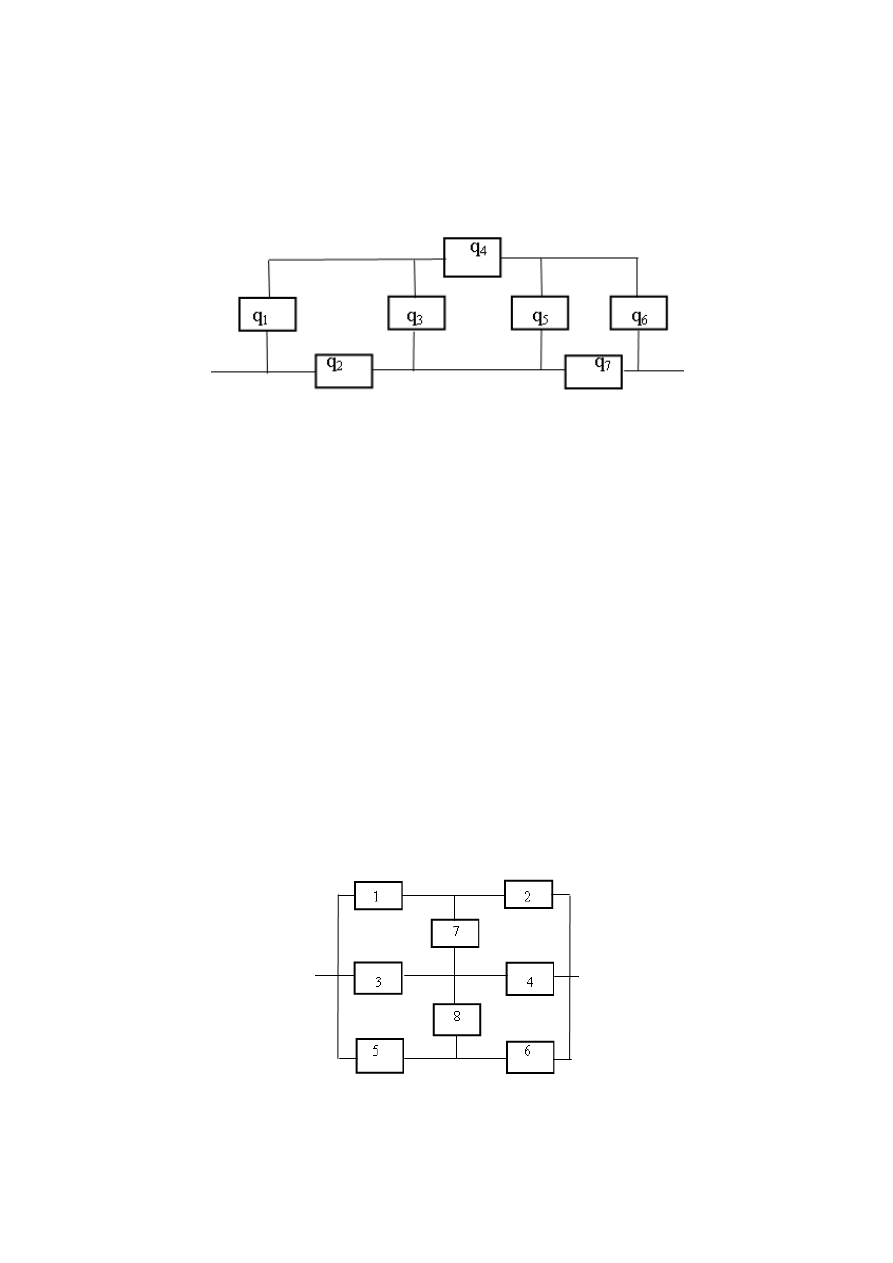
6. Структурная схема надёжности системы имеет вид «сложного
мостика», показанного на рис. 1.1.
Рис. 1.1. Структурная схема надёжности системы
Для элементов 1, 5:
4
1
,
10
ч ,
0,8;
t
P t
e
3, 6:
2
4
1
,
4 10
ч
t
P t
e
.
Элемент 4 имеет нормальное распределение времени безотказной
работы с параметрами
2000 ч,
200 ч;
t
t
m
элементы 2 и 7 имеют
экспоненциальное распределение с интенсивностью
4
1
2
3,5 10 ч ,
5
1
7
8 10
ч .
Определите вероятность безотказной работы системы в момент
времени t = 1 500 часов.
7. Найти вероятность безотказной работы за время наработки
в 100 часов системы, имеющей структурную схему надежности
(рис. 1.2), если для звеньев 1, 2, 3, 4, 5, 6
95
,
0
P
. Для звена 7 веро-
ятность безотказной работы определяется по закону Вейбулла с пара-
метрами
0,5
;
1
0,0015 ч ;
для звена 8 – по закону Рэлея с пара-
метром
3
1
2,5 10
ч
.
Рис. 1.2. Структурная схема надёжности системы
5
Тема 3. Основные вопросы эксплуатационной надёжности тех-
нических систем
8. Система состоит из 10 равнонадежных элементов, вреднее время
безотказной работы элемента равна T = 1000 ч. Предполагается, что
справедлив экспоненциальный закон надежности для элементов систе-
мы и основная и резервная системы равнонадежны. Необходимо найти
среднее время безотказной работы системы T
S
, частоту отказов a
S
(t)
и интенсивность отказов
( )
S
t
в момент времени t = 50 ч в следующих
случаях:
а) нерезервированной системы;
б) дублированной системы при постоянно включенном резерве.
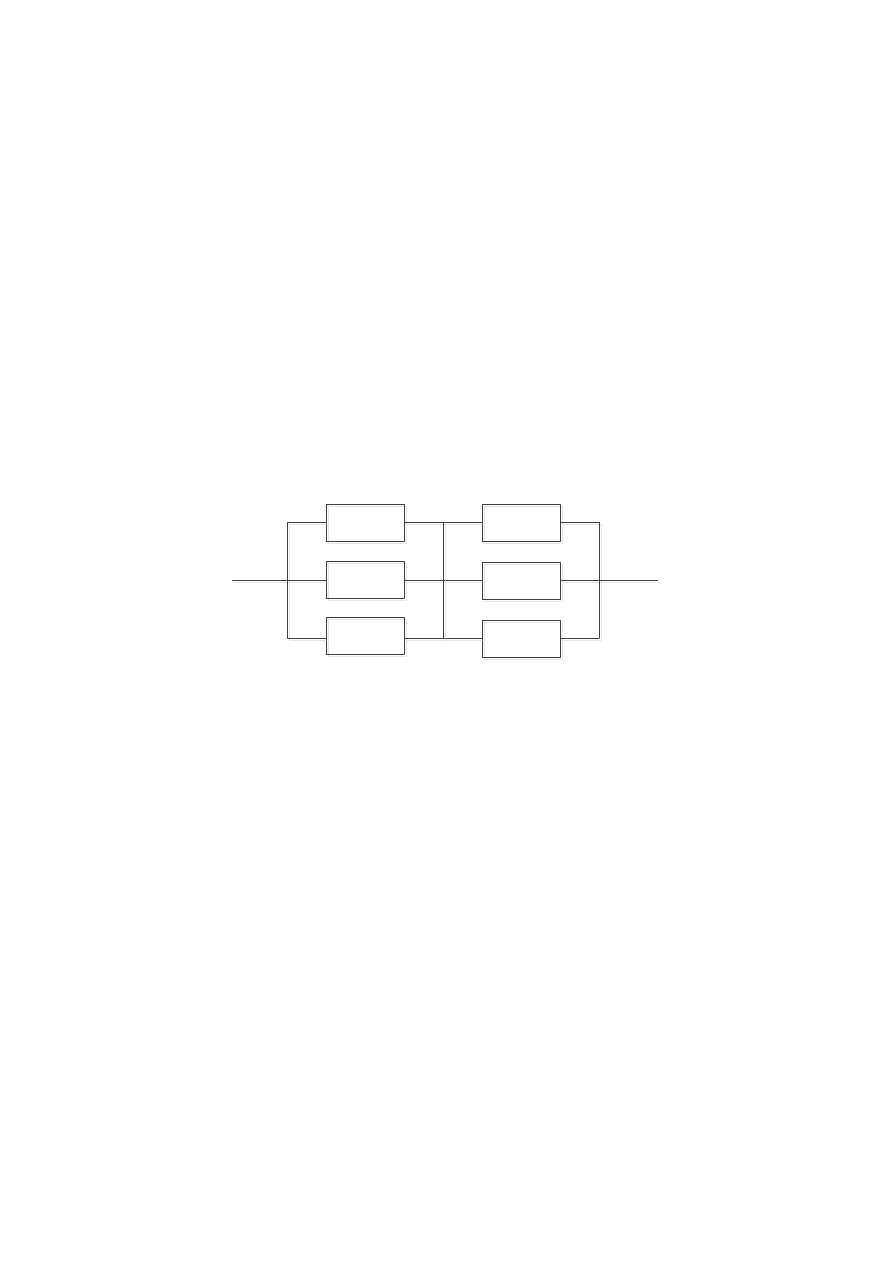
9. Схема расчета надежности изделия приведена на рис. 1.3. Найти
вероятность безотказной работы изделия, если известны вероятности
безотказной работы элементов:
1
0,9
P
,
2
0,8
P
.
P
1
P
1
P
1
P
2
P
2
P
2
Рис. 1.3. Структурная схема надёжности системы
10. Не резервированное устройство управления состоит из 400 рав-
но надёжных элементов. Для повышения надёжности системы предпо-
лагается провести пассивное раздельное дублирование всех элементов.
Рассчитайте интенсивность отказов одного элемента, чтобы система
имела вероятность безотказной работы
0,95,
10 ч
P
, если функ-
цией распределения времени безотказной работы элемента является
распределение Рэлея.
Тема 4. Диагностика автоматизированных систем
11. При испытаниях партии исполнительных механизмов (ИМ) из
6 штук было установлено, что погрешность позиционирования со време-
нем увеличивается. Данные о погрешностях, полученные для моментов
времени эксплуатации t
1
= 0 ч, t
2
= 50 + 12·N ч приведены в табл. 1.2.