Файл: Лабораторный практикум по информатике. Работа в WORD.docx
Добавлен: 28.11.2018
Просмотров: 1855
Скачиваний: 17
-
Аппроксимация функции.
Исходная функция аппроксимируется в соответствии с заданием функциями:
- y=mx+b - линейная;
- y=bmx - логарифмическая.
Задача сводится к нахождению коэффициентов «m» и «b». Для нахождения этих коэффициентов в зависимости от вида аппроксимации используются функции: «ЛИНЕЙН» и «ЛГРФПРИБЛ». Результатом этих функций является массив коэффициентов «m» и «b». Для выбора из массива требуемого коэффициента используется функция «ИНДЕКС», которая позволяет по номеру строки и столбца выбрать из массива требуемую величину.
Функция «ИНДЕКС» имеет две синтаксические формы, в данном случае выбирается форма: «массив; номер строки; номер столбца»).
В окне функции «ИНДЕКС» в поле «Номер строки» поставить цифру 1 для нахождения коэффициента «m» и 2 - для нахождения «b». В поле «Массив» помещается функция «ЛИНЕЙН» или «ЛГРФПРИБЛ».
В окне функции «ЛИНЕЙН» или «ЛГРФПРИБЛ». в полях «Изв_знач_у» и «Изв_знач_х» указать соответствующие области таблицы табуляции исходной функции. Поля «Константа» и «Стат» не заполняются.
ПРИМЕЧАНИЕ. Логарифмическая функция не имеет отрицательного значения. Если исходная функция имеет отрицательные, то при нахождении коэффициентов логарифмического приближения вместо числового значения будет выводиться «ЧИСЛО». В этом случае исходную функцию надо взять по абсолютной величине (=ABS(f)).
Отклонения аппроксимирующих функций находится как разность между исходной функцией и аппроксимирующей.
-
Среднее отклонение и дисперсия отклонения.
Среднее отклонение находится как среднее арифметическое всех отклонений. Для расчета используется функция «СРЗНАЧ».
Дисперсия D случайной величины определяется формулой:
D = M( – M)2
Дисперсия случайной величины — это математическое ожидание квадрата отклонения случайной величины от её математического ожидания.
Для расчета дисперсии отклонения в EXCEL использовать функции и «ДИСП».
ПРИЛОЖЕНИЕ 1
НЕФОРМАТИРОВАННЫЙ МАКЕТ ОТЧЕТА
ЗАДАНИЕ К ЛАБОРАТОРНОМУ ПРАКТИКУМУ
Решение уравнений и аппроксимация функций
Обработка таблицы
Лабораторная работа № 1. РЕШЕНИЕ УРАВНЕНИЯ
Графическое решение уравнения
Точное решение
Режим формул
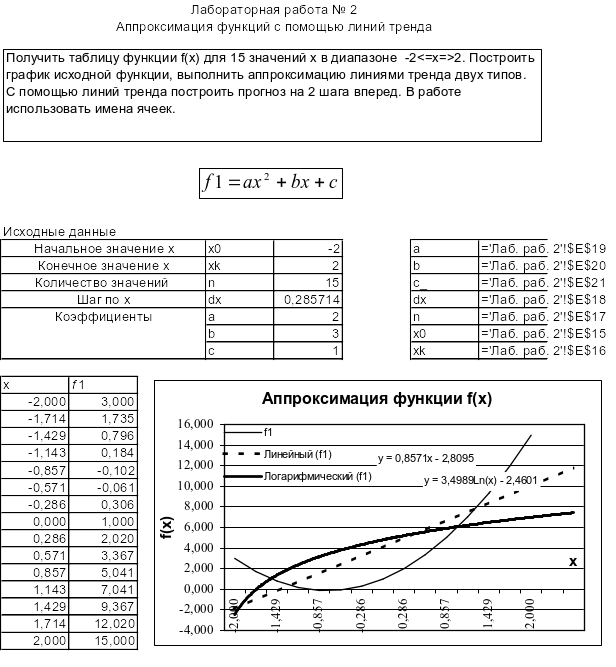
Лабораторная работа № 2. АППРОКСИМАЦИЯ ФУНКЦИЙ С ПОМОЩЬЮ ЛИНИИ ТРЕНДА
Режим значений
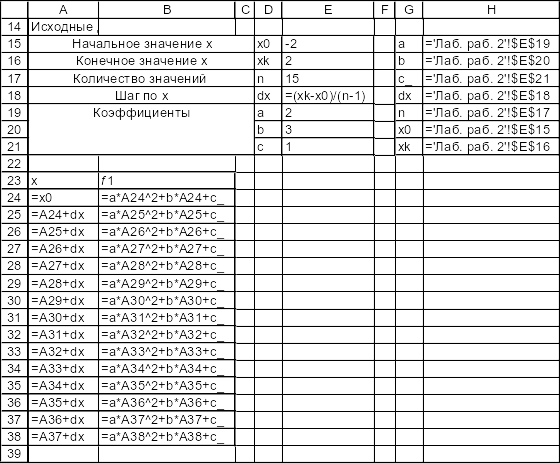
Режим формул
Лабораторная работа № 3. АППРОКСИМАЦИЯ ФУНКЦИИ
Режим значений
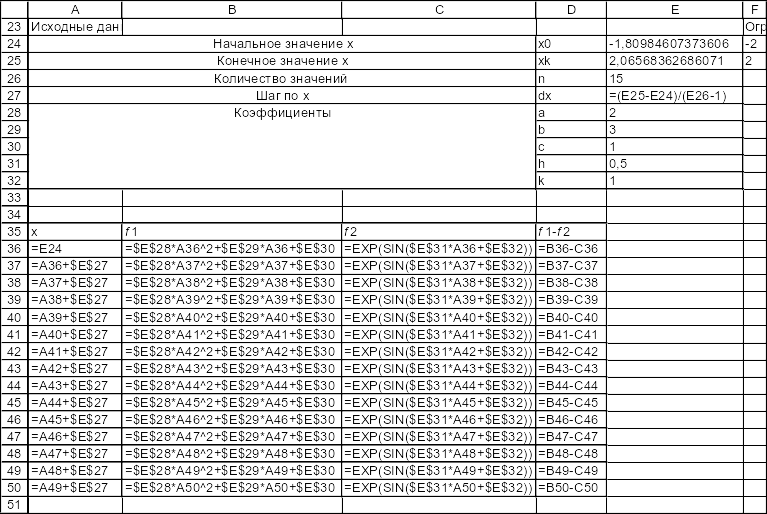
Режим формул
Лабораторная работа № 4. ОБРАБОТКА ТАБЛИЦ
Режим значений
Диаграммы
Режим формул
Лабораторная работа № 5. ФИЛЬТРАЦИЯ ДАННЫХ. АВТОФИЛЬТР
Исходная таблица
Фильтрация по точному значению
Фильтрация по шаблону
Фильтрация по диапазону значений
Лабораторная работа № 6. ФИЛЬТРАЦИЯ ДАННЫХ. РАСШИРЕННЫЙ ФИЛЬТР
Исходная таблица
Фильтрация по числовому условию
Критерий «или»
Критерий «и»
Вычисляемый критерий
Вычисляемый критерий в режиме формул
Лабораторная работа № 7. СОРТИРОВКА ТАБЛИЦ
Исходная таблица
Сортировка по текстовому столбцу
Сортировка по числовому столбцу
Сортировка по двум столбцам
Сортировка по пользовательскому списку
Лабораторная работа № 8. ПОДВЕДЕНИЕ ИТОГОВ В ТАБЛИЦЕ
Исходная таблица
Суммарные показатели
Максимальные показатели
Лабораторная работа № 9. НЕСВЯЗАННАЯ КОНСОЛИДАЦИЯ ТАБЛИЦ
Исходные таблицы
Несвязанная консолидация
Лабораторная работа № 10. СВЯЗАННАЯ КОНСОЛИДАЦИЯ ТАБЛИЦ
Режим значений
Режим формул
Лабораторная работа № 11. СВОДНЫЕ ТАБЛИЦЫ
Исходные таблицы
Сводная таблица по одной таблице
Консолидация таблиц
Лабораторная работа № 12. ИСПОЛЬЗОВАНИЕ ЭЛЕМЕНТОВ УПРАВЛЕНИЯ И МАКРОСОВ
Режим значений
Режим формул
ЛИТЕРАТУРА
ЗАДАНИЯ К ЛАБОРАТОРНОМУ ПРАКТИКУМУ
Решение уравнений
и аппроксимация
(лабораторные работы
1-3)
Варианты 1-16
|
Вариант |
f(x)=ax2+bx+c |
f2(x)=esin(gx+k) |
||||
|
а |
b |
с |
g |
k |
||
|
1 |
2 |
3 |
1 |
0,5 |
1 |
|
|
2 |
1 |
-3 |
0,1 |
0,5 |
2 |
|
|
3 |
2 |
2 |
-1 |
1 |
5 |
|
|
4 |
2 |
-0,5 |
-1 |
2 |
4 |
|
|
5 |
-4 |
1 |
1 |
3 |
3 |
|
|
6 |
-4 |
-2 |
1 |
4 |
2 |
|
|
7 |
-5 |
-3 |
5 |
5 |
1 |
|
|
8 |
-4 |
2 |
4 |
1 |
1 |
|
|
9 |
2 |
3 |
1 |
2 |
2 |
|
|
10 |
1 |
-3 |
0,1 |
3 |
3 |
|
|
11 |
2 |
2 |
-1 |
4 |
4 |
|
|
12 |
2 |
-0,5 |
-1 |
5 |
5 |
|
|
13 |
-4 |
1 |
2 |
-2 |
-2 |
|
|
14 |
-4 |
-2 |
1 |
-3 |
2 |
|
|
15 |
-5 |
-3 |
1 |
-4 |
3 |
|
|
16 |
7 |
2 |
-1 |
-5 |
4 |
|
Варианты 17-30
|
Вариант |
f(x)=ax2+bx+c |
f3(x)=mx3 +px2+qx+r |
|||||
|
а |
b |
с |
m |
p |
q |
r |
|
|
17 |
2 |
3 |
1 |
-1 |
1 |
-2 |
-5 |
|
18 |
1 |
-3 |
0,1 |
-1 |
1 |
-2 |
-5 |
|
19 |
2 |
2 |
-1 |
-1 |
1 |
-2 |
-5 |
|
20 |
2 |
-0,5 |
-1 |
-1 |
1 |
-2 |
-5 |
|
21 |
-4 |
1 |
1 |
-1 |
1 |
-2 |
-5 |
|
22 |
-4 |
-2 |
1 |
-1 |
1 |
-2 |
-5 |
|
23 |
-5 |
-3 |
-1 |
-1 |
1 |
-2 |
-5 |
|
24 |
-4 |
2 |
-1 |
-1 |
1 |
-2 |
-5 |
|
25 |
2 |
3 |
1 |
2 |
1 |
-3 |
1 |
|
26 |
1 |
-3 |
0,1 |
2 |
1 |
-3 |
-5 |
|
27 |
2 |
2 |
-5 |
2 |
1 |
-3 |
-5 |
|
28 |
2 |
-0.5 |
-7 |
2 |
1 |
-3 |
-5 |
|
29 |
-4 |
1 |
1 |
2 |
1 |
-3 |
-5 |
|
30 |
-4 |
-2 |
1 |
2 |
1 |
-3 |
-5 |
ПРИЛОЖЕНИЕ
3
Международный
институт рынка
Факультет экономики
и менеджмента
Кафедра информационных
систем и компьютерных технологий
Отчет
о лабораторном практикуме
по
табличному процессору EXCEL
Выполнил
Сидоров В.А.
группа
М-11
Проверил
оценка
дата
Самара
2015
ЗАДАНИЕ К ЛАБОРАТОРНОМУ ПРАКТИКУМУ
1. Лабораторная работа № 1. РЕШЕНИЕ УРАВНЕНИЯ

2. Лабораторная работа № 2. АППРОКСИМАЦИЯ ФУНКЦИЙ С ПОМОЩЬЮ ЛИНИИ ТРЕНДА