ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 6264
Скачиваний: 13

76
Пример 7. 12-значное двоичное число разделили на две
равные части: левая часть a, правая — b. Сколько существует
12-значных двоичных чисел, для которых выполняется условие:
b
a
+ = 111111, т.е. арифметическая сумма чисел a и b есть шес-
тизначное двоичное число без нулей?
Решение. Равенство вида
b
a
+ = 111111 выполняется толь-
ко в том случае, когда числа a и b являются взаимно инверсны-
ми, т.е. переходят одно в другое заменой всех единиц нулями и
всех нулей единицами. Следовательно, если выбрано число a, то
ему может быть поставлено в соответствие только одно число b.
Всего существует 64 числа, которые могут быть записаны в ле-
вой части. Столько же существует и искомых 12-значных чисел.
Ответ: 64.
Пример 8. 11-значное двоичное число c разделили на две
части a и b так, что в левой части точно пять знаков. Сколько
всего существует 11-значных чисел, для которых выполняется
условие: a > b.
Решение. Рассуждаем следующим образом. Если a = 0, то
неравенство a > b невозможно. При a = 1 существует одно зна-
чение c: 00001 000000. При a = 2 существует два значения c:
00010 000000 и 00010 000001. При a = 3 существует три значе-
ния c и так далее до a = 31, что дает 31 значение c. Всего:
1 + 2 + 3 + … + 31 = 496.
Ответ: 496.
Найденный ответ можно проверить, если решить еще две
задачи: найти количество 11-значных чисел, для которых вы-
полняется условие: a = b и a < b.
Если a = b, то существует 32 искомых числа.
Если a < b, то рассуждаем по аналогии с исходной задачей:
при a = 0 количество искомых чисел равно 63; при a = 1 их ко-
личество равно 62 и так далее до a = 31, которое дает 32 иско-
мых числа. Всего:
63 + 62 + 61 + … + 32 = 1520.
Сложим результаты вычислений для a > b, a = b и a < b:
496 + 32 + 1520 = 2048,
т.е. столько, сколько существует 11-значных двоичных чисел.
77
óÄëíú 5
íÖéêàü ÉêÄîéÇ
1 Ç‚Ó‰Ì˚ Á‡Ï˜‡ÌËfl
По теории графов предусмотрено два тестовых задания и
одна задача из письменной контрольной работы.
Темы тестов: «Кодирование деревьев» и «Эйлеровы графы».
Чтобы успешно пройти первый тест, студент должен иметь
представление о таких понятиях, как инцидентность, деревья и
леса, связность графа, достижимость в графе, циклы, висячие
вершины, помеченные графы.
Второй тест охватывает дополнительный круг понятий. Это
эйлеровы и полуэйлеровы графы, обход графа, четность и не-
четность степени вершины, уникурсальная линия, замкнутые и
разомкнутые простые цепи.
Задача из контрольной работы предусматривает умение на-
ходить:
а) все простые цепи, соединяющие две вершины неориен-
тированного графа;
б) все простые циклы, начинающиеся и оканчивающиеся в
заданной вершине неориентированного графа;
в) все простые цепи, соединяющие две вершины орграфа
(ориентированного графа).
2 íÂÒÚ˚ ÔÓ ÚÂÓðËË „ð‡ÙÓ‚
2.1 Тесты по теме № 9 «Кодирование деревьев»
Последовательность действий при ко-
дировании деревьев (методом Пруфера)
поясним на примерах.
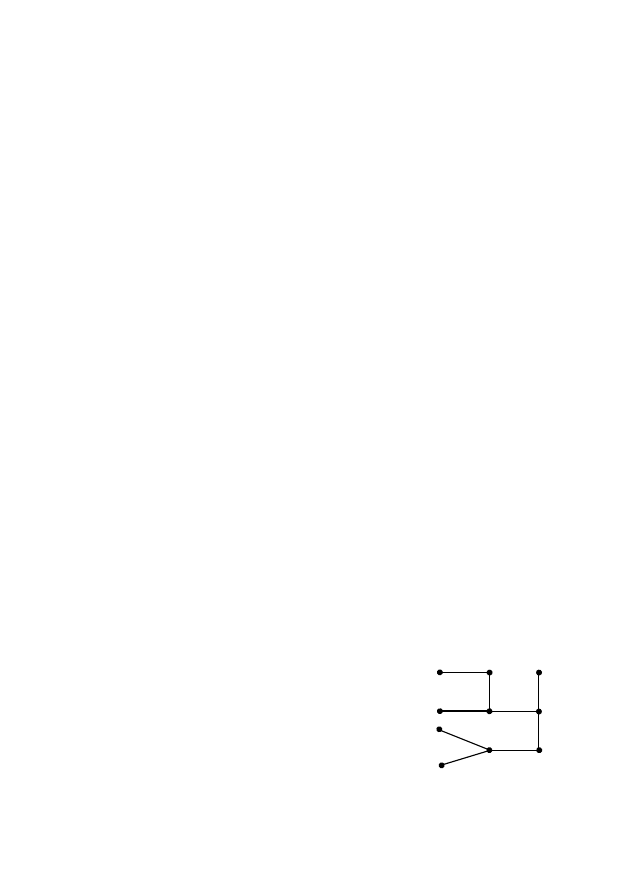
Пример 1. Найти код дерева, пред-
ставленного на рис. 1.
Решение. Находим висячую вершину с
наименьшим номером. Это вершина 3.
Удаляем вершину 3 вместе с ребром. Но-
5
6
7
8
9
4
3
2
1
Рис. 1
10
78
мер вершины, инцидентной удаленному ребру, есть первая циф-
ра искомого кода. Это цифра 2.
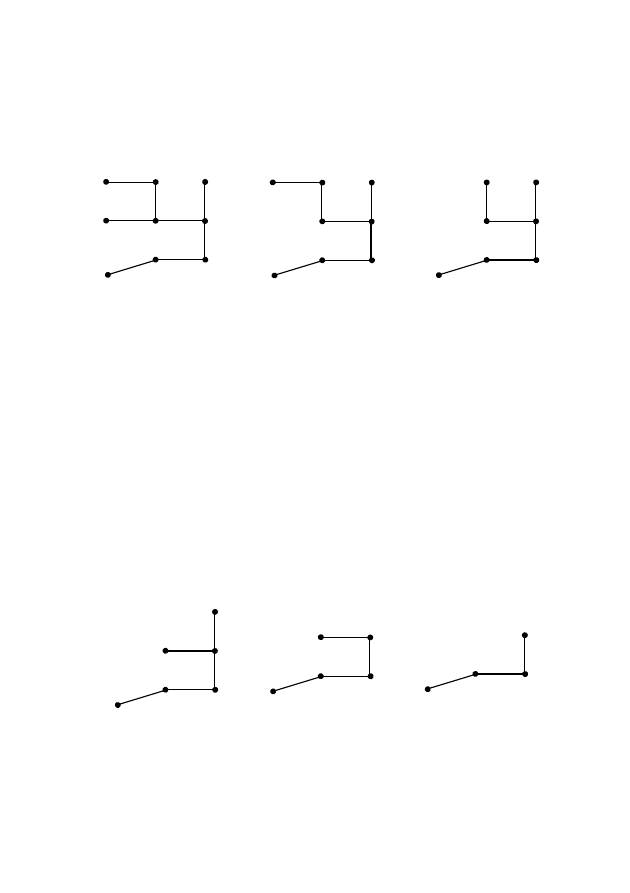
Получился новый граф, изображенный на рис. 2.
5
6
7
8
9
4
2
1
Рис. 2
10
5
6
7
8
9
2
1
Рис. 3
10
6
7
8
9
2
1
Рис. 4
10
В новом графе (рис. 2) содержится четыре висячих верши-
ны: 4, 5, 7 и 10. Вершину с наименьшим номером, т.е. вершину
4, удаляем ее вместе с ребром. Вершина, инцидентная удален-
ному ребру, имеет номер 9. Следовательно, цифра 9 — это вто-
рой знак искомого кода.
В результате удаления ребра 4–9 получился очередной
граф, приведенный на рис. 3. В этом графе три висячие вершины
с номерами: 5, 7 и 10. Наименьшим из них является номер 5.
Удаляем вершину 5 вместе с ребром и получаем третий знак ко-
да — цифру 6.
Новый граф приведен на рис. 4. В этом графе три висячие
вершины. Наименьший номер — 6. Четвертый знак искомого
кода — цифра 9.
7
8
9
2
1
Рис. 5
10
8
9
2
1
Рис. 6
10
8
2
1
Рис. 7
10
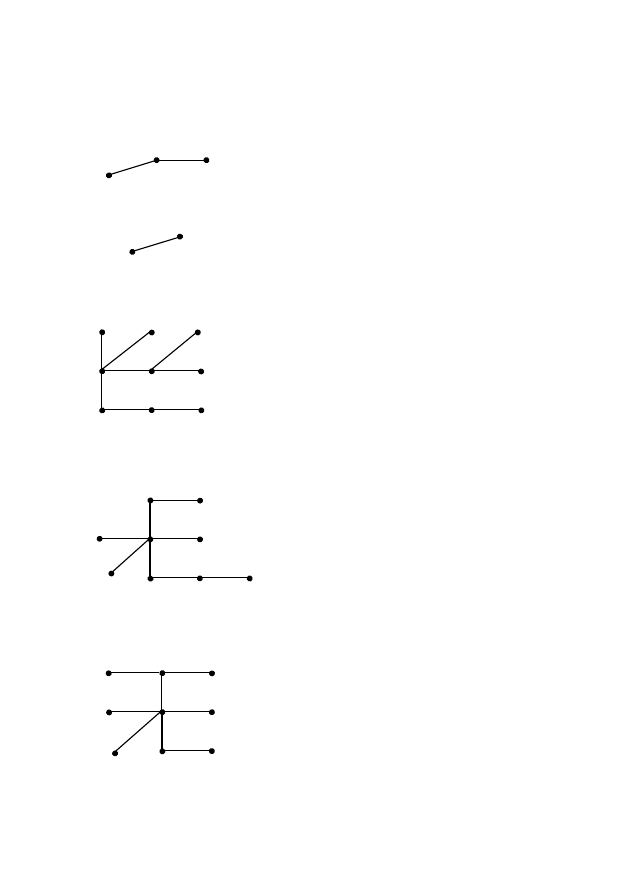
На рис. 5 удаляем вершину 7 и получаем пятый знак кода.
Это цифра 8.
79
На рис. 6 удаляем вершину 9. Цифра 8 — это шестой знак кода.
На рис. 7 удаляем вершину 8. Цифра 1 — это седьмой знак
кода.
На рис. 8 удаляем вершину 1
вместе с ребром 1–2. Цифра 2 — это
восьмой знак искомого кода. После
удаления вершины 1 получился граф,
состоящий из двух вершин и одного
ребра (рис. 9). Когда получается такой
граф, кодирование заканчивается.
Таким образом, искомый код
имеет вид: 29698812.
Ответ: 29698812.
Пример 2. Найти код дерева,
изображенного на рис. 10.
Решение. В этом графе искомый
код начинается с цифры 2. Действуя
точно так же, как и в предыдущем
примере, получаем: 2344499.
Ответ: 2344499.
Пример 3. Найти код дерева,
приведенного на рис. 11.
Решение. В графах на рис. 10 и
11 содержится цепь 1–2–3–4, окан-
чивающаяся висячей вершиной с
наименьшим номером, равным 1. В
связи с этим первые три знака кодов
обоих графов совпадают. Но затем
равенство знаков в кодах нарушает-
ся, и код дерева, приведенного на
рис. 11, принимает вид 2345444.
Ответ: 2345444.
Пример 4. Найти код дерева,
изображенного на рис. 12.
Решение. Действуя как и в пре-
дыдущих случаях, начиная с наи-
меньшего номера висячей вершины,
получаем искомый код: 4345544.
5
6
7
8
9
4
3
2
1
Рис. 10
5
6
7
8
9
4
3
2
1
Рис. 11
5
6
7
8
9
4
3
2
1
Рис. 12
2
1
Рис. 8
10
2
Рис. 9
10
80
2.2 Тест по теме № 10 «Эйлеровы графы»
Признак, при помощи которого выявляются эйлеровы гра-
фы, прост: граф называется эйлеровым, если в нем нет нечетных
вершин. Кроме того, существует понятие полуэйлерового графа:
граф называется полуэйлеровым, если в нем точно две нечетные
вершины.
Тест состоит в выборе из заданного набора графов сначала
всех эйлеровых, а затем — всех полуэйлеровых графов.
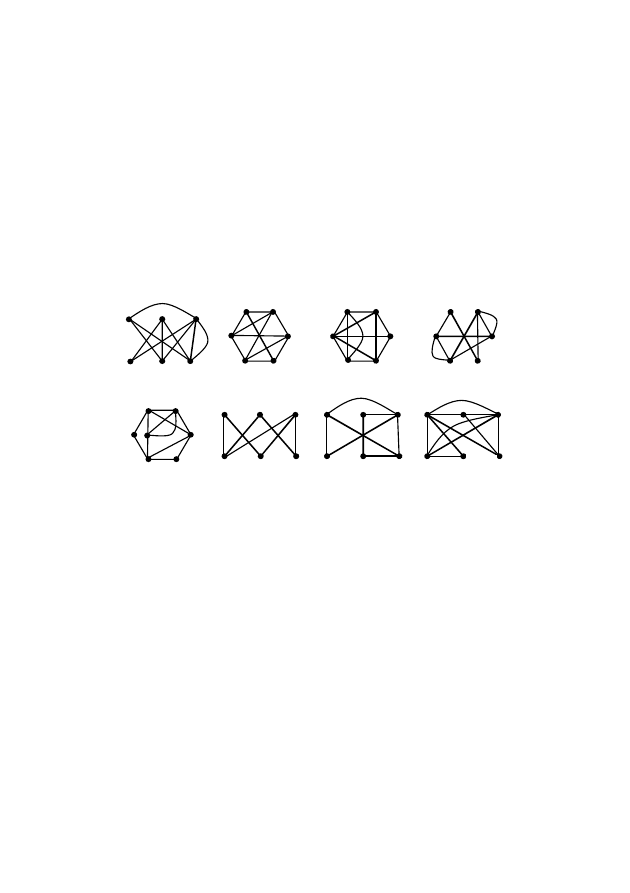
Пример. Укажите сначала номера всех эйлеровых графов, а
затем — всех полуэйлеровых (рис. 13).
1
2
3
4
5
6
7
8
Рис. 13
Решение. В графе 1 четыре нечетные вершины, следова-
тельно, он не является эйлеровым и не является полуэйлеровым.
В графе 2 две нечетные вершины. Это полуэйлеров граф. Третий
граф содержит две нечетные вершины: степень одной из них
равна 3, другой — 5. Граф является полуэйлеровым. В четвер-
том графе все вершины являются четными, следовательно, это
эйлеров граф. В графе 5 также нет нечетных вершин, поэтому
граф 5 является эйлеровым. Граф 6 — полуэйлеров, так как в
нем только две нечетные вершины. Две нечетные вершины со-
держится и в графе 7. Следовательно, граф 7 — полуэйлеров. В
графе 8 четыре нечетные вершины. Этот граф не относится ни к
эйлеровым, ни к полуэйлеровым.
Ответ:
Номера эйлеровых графов: 4, 5;
Номера полуэйлеровых графов: 2, 3, 6, 7.