ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 6259
Скачиваний: 13

81
3 ᇉ‡˜Ë ËÁ письменной ÍÓÌÚðÓθÌÓÈ ð‡·ÓÚ˚.
íÂχ 10: «ç‡ıÓʉÂÌË ÔðÓÒÚ˚ı ˆÂÔÂÈ
‚ „ð‡Ù»
3.1 Содержание работы
Задача по теории графов, входящая во вторую контрольную
работу, состоит из трех пунктов.
По первому из них требуется найти все простые цепи, со-
единяющие две заданные вершины неориентированного графа.
В разных вариантах контрольной работы заданными могут быть
различные вершины, например 1 и 6 либо 2 и 4 и т.д. В данном
же случае для определенности заданными будем считать вер-
шины 1 и 5. Тогда тему контрольной работы можно сформули-
ровать следующим образом: найти все простые цепи, соеди-
няющие вершины 1 и 5 неориентированного графа, заданного
множеством ребер:
G = {{1,2}, {1,3}, {1,4}, {1,5},
{2,3}, {2,4}, {3,4}, {3,5}, {4,5}}.
Для решения задачи сначала следует построить граф. Для
этого в выражении G имеется полная информация. Из записи G
видно, что в графе пять вершин:
V = {1, 2, 3, 4, 5},
где V — множество вершин графа.
Элементами множества G являются
ребра графа, заданные подмножествами
множества V, содержащими по два эле-
мента. Например, первое подмножество
имеет вид {1,2}. Эта запись обозначает:
вершины 1 и 2 соединены ребром. Точно
так же интерпретируются все остальные
элементы множества G.
Граф изображен на рис. 14.
По второму пункту задачи для того
же неориентированного графа требуется найти все простые цик-
лы, которые начинаются в вершине 1 и в ней же оканчиваются.
По третьему пункту задача формулируется как и первая, но
при условии, что граф является ориентированным (орграфом),
3
1
4
5
2
Рис. 14

82
т.е. теперь надо считать, что в множестве G перечислены не
ребра графа, а дуги, где первая цифра — начало дуги. Например,
запись {1,2} обозначает: дуга соединяет вершины 1 и 2, при
этом стрелка направлена от вершины 1 к вершине 2.
В следующих трех подразделах приведены образцы реше-
ния всех трех пунктов задачи о поиске всех простых цепей.
3.2 Простые цепи в неориентированном графе
Применение алгоритма нахождения всех простых цепей,
соединяющих две заданные вершины графа, проиллюстрируем
на примере графа, изображенного на рис. 14. При этом будем
полагать, что заданными являются вершины 1 и 5 и что началь-
ной является вершина 1, а конечной — вершина 5. В общем же
случае, так как граф является неориентированным, начальной
можно объявить и пятую вершину, а конечной — первую. Ре-
зультаты от этого не изменятся.
•
На первом этапе найдем все варианты выхода из первой
вершины, т.е. найдем все простые цепи, выходящие из вершины
1 и содержащие точно по одному ребру:
1 – 2, 1 – 3, 1 – 4, 1 – 5.
Одна простая цепь, соединяющая вершины 1 и 5, найдена
(она подчеркнута).
•
На втором этапе найдем все простые цепи, содержащие
точно по два ребра и выходящие из вершины 1. Для этого вос-
пользуемся результатами предыдущего этапа:
1 – 2 – 3,
1 – 3 – 2,
1 – 4 – 2,
1 – 2 – 4,
1 – 3 – 4,
1 – 4 – 3,
1 – 3 – 5,
1 – 4 – 5.
Получены еще две искомые цепи (подчеркнуты).
•
На третьем этапе находим все простые цепи, ведущие из
вершины 1 и содержащие точно по три ребра. Для этого вос-
пользуемся результатами второго этапа:
1 – 2 – 3 – 4,
1 – 3 – 2 – 4,
1 – 4 – 2 – 3,
1 – 2 – 3 – 5,
1 – 3 – 4 – 2,
1 – 4 – 3 – 2,
1 – 2 – 4 – 3,
1 – 3 – 4 – 5,
1 – 4 – 3 – 5,
1 – 2 – 4 – 5.

83
На третьем этапе получено еще четыре искомых цепи. Все
они подчеркнуты.
•
Четвертый этап в случае данного графа является послед-
ним:
1 – 2 – 3 – 4 – 5,
1 – 3 – 2 – 4 – 5,
1 – 4 – 2 – 3 – 5,
1 – 2 – 4 – 3 – 5,
1 – 3 – 4 – 2 – ?
1 – 4 – 3 – 2 – ?
На последнем этапе получено четыре простые цепи из ис-
комых. Это самые длинные простые цепи. Они проходят через
все вершины графа.
Две последние цепи оканчиваются вопросительным знаком.
Это значит, что они являются тупиковыми, так как любое дви-
жение из вершины 2 приводит к повтору номеров вершин, в ре-
зультате чего появляется цикл. Все подобные цепи удаляем.
3.3 Простые циклы в неориентированном графе
Эта задача решается точно так же, как и предыдущая. Ре-
шение ее проиллюстрируем на примере графа, изображенного
на рис. 14.
На первом этапе найдем все простые цепи, выходящие из
вершины 1 и содержащие точно по одному ребру:
1 – 2, 1 – 3, 1 – 4, 1 – 5.
На втором этапе найдем все простые цепи, выходящие из
вершины 1 и содержащие точно по два ребра:
1 – 2 – 1,
1 – 3 – 1,
1 – 4 – 1,
1 – 5 – 1,
1 – 2 – 3,
1 – 3 – 2,
1 – 4 – 2,
1 – 5 – 3,
1 – 2 – 4,
1 – 3 – 4,
1 – 4 – 3,
1 – 5 – 4,
1 – 3 – 5,
1 – 4 – 5.
Найдено четыре простых цикла, правда, содержащих по два
ребра (подчеркнуты). Но формально и они удовлетворяют опре-
делению простого цикла: если в простой цепи при вершинном
ее представлении (т.е. в виде последовательности номеров вер-
шин) первая и последняя вершины совпадают, то цепь называ-
ется простым циклом.
Третий этап:

84
1 – 2 – 3 – 1,
1 – 3 – 2 – 1,
1 – 4 – 2 – 1, 1 – 5 – 3 – 1,
1 – 2 – 3 – 4,
1 – 3 – 2 – 4,
1 – 4 – 2 – 3, 1 – 5 – 3 – 2,
1 – 2 – 3 – 5,
1 – 3 – 4 – 1,
1 – 4 – 3 – 1,
1 – 5 – 3 – 4,
1 – 2 – 4 – 1,
1 – 3 – 4 – 2,
1 – 4 – 3 – 2,
1 – 5 – 4 – 1,
1 – 2 – 4 – 3,
1 – 3 – 4 – 5,
1 – 4 – 3 – 5, 1 – 5 – 4 – 2,
1 – 2 – 4 – 5,
1 – 3 – 5 – 1,
1 – 4 – 5 – 1,
1 – 5 – 4 – 3,
1 – 3 – 5 – 4,
1 – 4 – 5 – 3.
На третьем этапе получено десять искомых простых цик-
лов, содержащих по три ребра.
Четвертый этап дает 16 новых простых циклов:
1 – 2 – 3 – 4 – 1,
1 – 3 – 2 – 4 – 1,
1 – 4 – 2 – 3 – 1,
1 – 2 – 3 – 4 – 5,
1 – 3 – 2 – 4 – 5,
1 – 4 – 2 – 3 – 5,
1 – 2 – 3 – 5 – 1,
1 – 3 – 4 – 2 – 1,
1 – 4 – 3 – 2 – 1,
1 – 2 – 3 – 5 – 4,
1 – 3 – 4 – 5 – 1,
1 – 4 – 3 – 5 – 1,
1 – 2 – 4 – 3 – 1,
1 – 3 – 5 – 4 – 1,
1 – 4 – 5 – 3 – 1,
1 – 2 – 4 – 3 – 5,
1 – 3 – 5 – 4 – 2,
1 – 4 – 5 – 3 – 2,
1 – 2 – 4 – 5 – 1,
1 – 5 – 3 – 2 – 1,
1 – 5 – 4 – 2 – 1,
1 – 2 – 4 – 5 – 3,
1 – 5 – 3 – 2 – 4,
1 – 5 – 4 – 2 – 3,
1 – 5 – 3 – 4 – 1,
1 – 5 – 4 – 3 – 1,
1 – 5 – 3 – 4 – 2,
1 – 5 – 4 – 3 – 2.
На заключительном (пятом) этапе получаем еще двенадцать
простых циклов. Особенность этих двенадцати циклов в том,
что они проходят через все вершины графа:
1 – 2 – 3 – 4 – 5 – 1,
1 – 3 – 2 – 4 – 5 – 1,
1 – 2 – 3 – 5 – 4 – 1,
1 – 3 – 5 – 4 – 2 – 1,
1 – 2 – 4 – 3 – 5 – 1,
1 – 4 – 5 – 3 – 2 – 1,
1 – 2 – 4 – 5 – 3 – 1,
1 – 5 – 4 – 2 – 3 – 1,
1 – 4 – 2 – 3 – 5 – 1,
1 – 5 – 4 – 3 – 2 – 1.
1 – 5 – 3 – 2 – 4 – 1,
1 – 5 – 3 – 4 – 2 – 1,
Таким образом, всего в графе, приведенном на рис. 1, суще-
ствует 42 простых цикла, начинающихся и оканчивающихся в
вершине 1. Из них 4 цикла содержат по два ребра (например, 1 –
2 – 1), 10 циклов – по три ребра (например, 1 – 2 – 3 – 1), 16
циклов — по четыре ребра (например, 1 – 2 – 3 – 4 – 1) и 12
циклов — по пять ребер (например, 1 – 2 – 3 – 4 – 5 – 1).
85
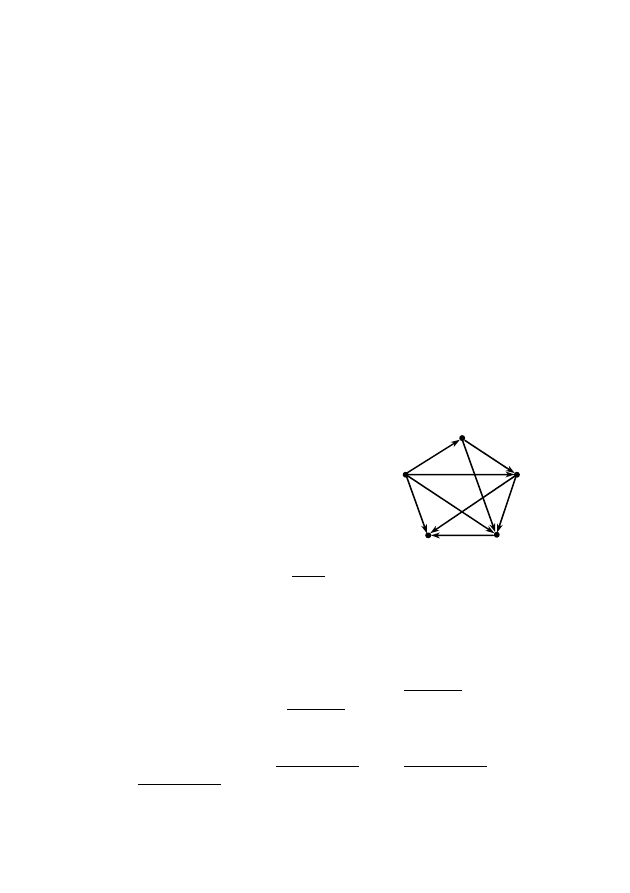
3.4 Простые цепи в ориентированном графе
В двух предыдущих случаях заданный граф считался не-
ориентированным. Теперь же будем считать, что он является
ориентированным и что каждая пара номеров вершин обознача-
ет не ребро, а дугу. При этом первая цифра в обозначении дуги
является ее началам, а вторая — концом.
Чтобы записать аналитическое выражение ориентированно-
го графа, вместо фигурных скобок, где указаны пары вершин,
следует поставить круглые скобки для обозначения того, что
записанные в них пары чисел являются упорядоченными. На-
пример:
G = {(1,2), (1,3), (1,4), (1,5),
(2,3), (2,4), (3,4), (3,5), (4,5)}.
Построим для этого выражения граф (рис. 15). Согласно за-
писи (1,2) проводим дугу от вершины 1 к вершине 2. Согласно
паре (1,3) проводим дугу от вершины 1 к вершине 3 и т.д.
В соответствии с заданием найдем
все простые цепи, соединяющие вер-
шины 1 и 5 этого орграфа. При их оты-
скании действуем точно так же, как и в
случае первой задачи, но с учетом ори-
ентации дуг.
Первый этап. Из вершины 1 выхо-
дит четыре дуги
1 – 2, 1 – 3, 1 – 4, 1 – 5.
Последняя из этих однореберных цепей оканчивается циф-
рой 5. Следовательно, одна из искомых простая цепь получена
(подчеркнута).
Второй этап. Находим все простые цепи, выходящие из
вершины 1 и состоящие из двух дуг:
1 – 2 – 3,
1 – 3 – 4,
1 – 4 – 5,
1 – 2 – 4,
1 – 3 – 5.
Получены еще две искомые цепи (обе подчеркнуты).
Третий этап:
1 – 2 – 3 – 4,
1 – 3 – 4 – 5,
1 – 2 – 4 – 5,
1 – 2 – 3 – 5.
3
1
4
5
2
Рис. 15