ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 6257
Скачиваний: 13

21
2.4 Тесты по теме № 5: «Алгебра Жегалкина»
Задание на тему «Алгебра Жегалкина» состоит в представ-
лении полинома Жегалкина в СДНФ. Ответом к тесту является
упорядоченный набор десятичных номеров минтермов, дизъ-
юнкция которых есть найденная СДНФ.
Для перевода полинома Жегалкина в СДНФ можно пользо-
ваться формулами вида:
P
Q
PQ
PQ
⊕ =
+
;
0.
P
P
⊕ =
Пример 1. Представить в СДНФ полином Жегалкина
.
f
AC
B
A
=
⊕ ⊕ (1)
Обозначим:
.
K
B
A
AB
AB
= ⊕ =
+
Тогда получим:
(
)
.
f
AC
K
ACK
ACK
A
C K
ACK
AK
CK
ACK
=
⊕ =
=
+
=
=
+
+
=
=
+
+
По теореме де Моргана находим :
K
.
K
AB
AB
=
+
Подставим это выражение в предыдущее:
(
)
(
)
(
)
.
f
A AB
AB
C AB
AB
AC AB
AB
AB
ABC
ABC
ABC
=
+
+
+
+
+
=
=
+
+
+
Заметим, что
.
AB
ABC
ABC
=
+
Подставив это выражение в предыдущее, получим искомую
СДНФ:
f
ABC
ABC
ABC
ABC
=
+
+
+
= (2, 3, 4, 7).
Полином Жегалкина можно найти и более простым путем.
Для этого достаточно каждую конъюнкцию представить в виде
дизъюнкции минтермов, объединив их знаками сложения по
модулю 2. В случае рассмотренного примера
AC = (5, 7); B = (2, 3, 6, 7); A = (4, 5, 6, 7).

22
Подставим эти выражения в (1) и удалим все пары одинако-
вых минтермов:
f = (5, 7)
⊕ (2, 3, 6, 7) ⊕ (4, 5, 6, 7) =
= (m
5
+ m
7
)
⊕ (m
2
+ m
3
+ m
6
+ m
7
)
⊕ (m
4
+ m
5
+ m
6
+ m
7
) =
= m
5
⊕ m
7
⊕ m
2
⊕ m
3
⊕ m
6
⊕ m
7
⊕ m
4
⊕ m
5
⊕ m
6
⊕ m
7
=
= m
2
⊕ m
3
⊕ m
4
⊕ m
7
= (2, 3, 4, 7).
Ответ: 2, 3, 4, 7.
Нахождение СДНФ на основе полинома Жегалкина можно
еще упростить, если воспользоваться картой Вейча. Напомним, что
при нанесении на карту Вейча полинома Жегалкина каждая конъ-
юнкция наносится на нее полностью, независимо одна от другой.
При этом в некоторых клетках может оказаться более чем по одной
единице. Нанесем на карту функцию (1). Получим рис. 1.
11
111
1
1
11
Рис. 1
1
1
1
Рис. 2
1
1
Строим новую карту (рис. 2), поставив в ней единицы в тех
клетках, где на рис. 1 находится нечетное число единиц. Из рис.
2 видно, что искомая СДНФ имеет вид:
f = (2, 3, 4, 7).
Ответ: 2, 3, 4, 7. (В компьютер вводим 2347.)
Пример 2. Представить в СДНФ полином Жегалкина:
.
AB
B
C
f
⊕
⊕
=
Решение. Наносим полином на карту Вейча (рис. 3).
11
111 11
1
1
Рис. 3
1
1
Рис. 4
1
1
1
На рис. 4 приведена искомая СДНФ.
Ответ: 1, 2, 5, 7. (В компьютер вводим 1257.)

23
Пример 3. Представить в СДНФ полином Жегалкина:
.
f
A
C
AB
= ⊕ ⊕
Решение. Наносим полином на карту Вейча (рис. 5).
11
111
1
1
Рис. 5
1
1
Рис. 6
1
1
1
11
На рис. 6 приведена искомая СДНФ.
Ответ: 1, 4, 5, 6. (В компьютер вводим 2456.)
Пример 4. Представить в СДНФ полином Жегалкина:
.
f
A
B
ВС
AB
= ⊕ ⊕
⊕
Решение. Наносим полином на карту Вейча (рис. 7).
Рис. 7
1
1
Рис. 8
1
1
111 1111
11
1
1
1
На рис. 8 приведена искомая СДНФ.
Ответ: 2, 4, 5, 6. (В компьютер вводим 2456).
3 Задачи из письменной кÓÌÚðÓθÌой ð‡·ÓÚ˚
3.1 Тема 2: «Минимизация нормальных форм»
Минимизировать булевы функции из данной контрольной
работы можно любым методом, но проще всего для этих целей
применить карту Вейча, так как упрощаемые функции зависят
только от четырех аргументов. Минимизацию дизъюнктивных и
конъюктивных нормативных форм с применением карт Вейча
проиллюстрируем несколькими примерами.

24
Пример 1. Найти минимальные ДНФ и КНФ следующей
функции, заданной в СДНФ:
f = (4, 5, 6, 7, 8, 10, 11, 12, 13, 14, 15).
Решение. Наносим функцию на карту Вейча (рис. 9). Ми-
нимальная ДНФ имеет вид:
.
f
B
AC
AD
= +
+
Чтобы найти КНФ, сначала минимизируем инверсию за-
данной функции. СДНФ ее инверсии приведена на рис 10. Ми-
нимальная ДНФ инверсии имеет вид:
.
f
AB
BCD
=
+
Рис. 9
1
1
1
1
1
1
1
1
1
1
1
Рис. 10
1
1
1
1
1
По теореме де Моргана инвертируем это выражение и по-
лучаем минимальную КНФ:
(
)(
).
f
A
B B
C
D
=
+
+ +
Ответ:
Минимальная ДНФ:
.
f
B
AC
AD
= +
+
Минимальная КНФ:
(
)(
).
f
A
B B
C
D
=
+
+ +
Пример 2. Найти минимальные ДНФ и КНФ следующей
функции, заданной в СДНФ:
f = (1, 2, 6, 7, 8, 10, 11, 12, 15).
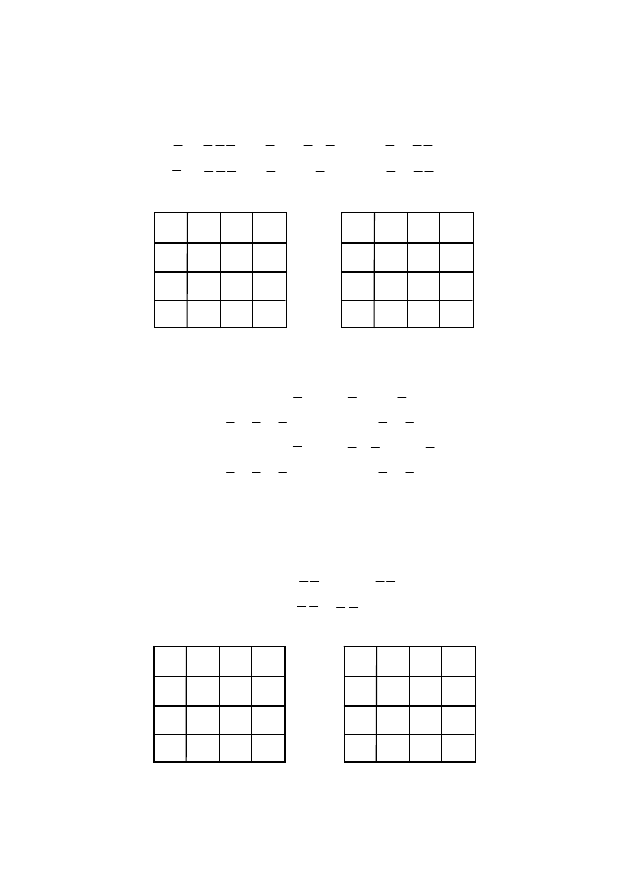
Решение. Наносим функцию на карту Вейча (рис. 11). Эта
функция имеет две минимальные ДНФ:
1
.
f
AC D
ABC
ACD
BCD
ABCD
=
+
+
+
+
2
.
f
ACD
ACD
BCD
ABC
ABCD
=
+
+
+
+
25
Для нахождения КНФ строим карту Вейча для инверсии за-
данной функции (рис. 12). Инверсия заданной функции также
имеет две минимальные ДНФ:
1
.
f
ACD
ACD
ABC
ABCD
ABCD
=
+
+
+
+
2
.
f
ACD
ACD
BCD
ABCD
ABCD
=
+
+
+
+
Рис. 12
1
1
1
1
Рис. 11
1
1
1
1
1
1
1
1
1
1
1
1
Соответственно получаем и две минимальные КНФ:
1
(
)(
)(
)
f
A C
D A
C
D A
B
C
=
+ +
+ +
+ +
&
&
(
)(
).
A
B
C
D A
B
C
D
+ + +
+ + +
2
(
)(
)(
)
f
A C
D A
C
D B
C
D
=
+ +
+ +
+ +
&
&
(
)(
).
A
B
C
D A
B
C
D
+ + +
+ + +
Пример 3. Найти минимальные ДНФ и КНФ:
f = (0, 1, 2, 3, 4, 5, 7, 8, 10, 11, 12, 13, 14, 15).
Решение. У данной функции (рис. 13) также не единствен-
ный вариант минимальной ДНФ. Приведем два из них:
.
f
AC
AB
BD
CD
=
+
+
+
.
f
AB
AC
B D
CD
=
+
+
+
Рис. 14
1
1
Рис. 13
1
1
1
1
1
1
1
1
1
1
1
1
1
1