ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 6258
Скачиваний: 13
26
Инверсия функции в минимальной ДНФ представима един-
ственным способом (рис. 14):
.
f
ABCD
ABCD
=
+
В соответствии с этим для заданной функции существует и
единственная минимальная КНФ:
(
)(
).
f
A
B
C
D A
B
C
D
=
+ + +
+ + +
Пример 4. Найти минимальные ДНФ и КНФ:
f = (0, 2, 3, 4, 5, 7, 8, 9, 10, 11, 13, 14, 15).
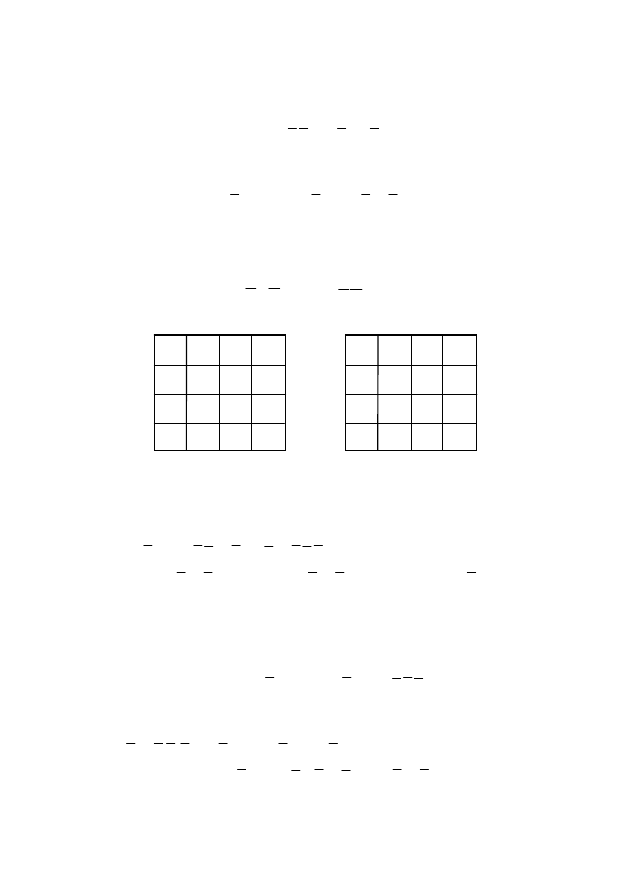
Решение. Одна из минимальных ДНФ имеет вид (рис. 15):
.
CD
AD
D
B
AC
C
B
A
f
+
+
+
+
=
Рис. 15
1
1
1
1
1
1
1
1
1
1
1
1
1
Рис. 16
1
1
1
Минимальная КНФ этой функции существует только одна
(рис. 16):
.
f
ABCD
ABCD
ABCD
=
+
+
(
)(
)(
).
f
A
B
C
D A
B
C
D A
B
C
D
=
+ + +
+ + +
+ + +
Пример 5. Найти минимальные ДНФ и КНФ:
f = (1, 2, 3, 5, 6, 7, 8, 13, 15).
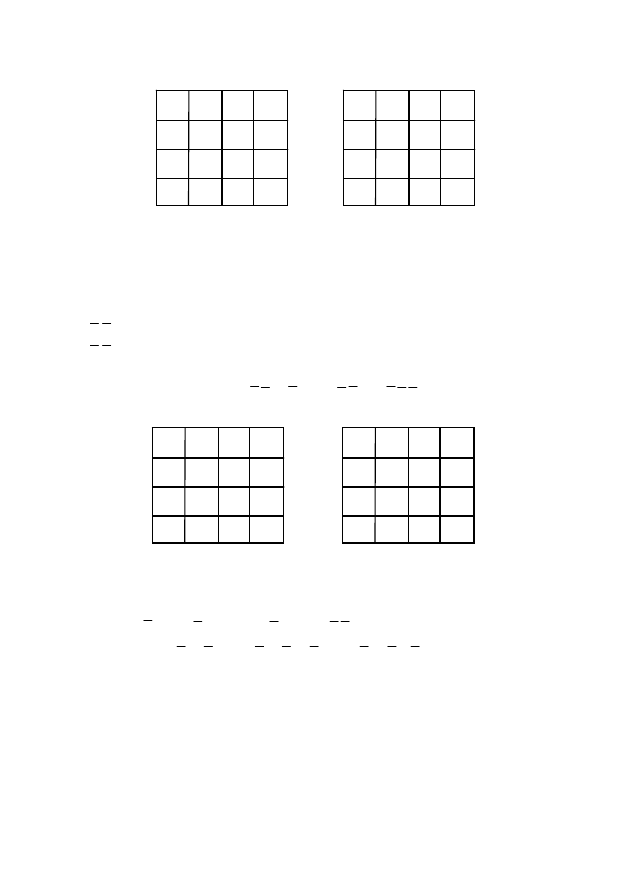
Решение. Существует единственная минимальная ДНФ
этой функции (рис. 17):
.
f
AC
BD
AD
ABCD
=
+
+
+
Минимальная КНФ представима не единственным спосо-
бом (рис. 18). Один из вариантов имеет вид:
.
f
AC D
ABD
ABD
ACD
=
+
+
+
(
)(
)(
)(
).
f
A C
D A
B
D A
B
D A
C
D
=
+ +
+ +
+ +
+ +
27
Рис. 17
1
1
1
1
1
1
1
1
1
Рис. 18
1
1
1
1
1
1
1
Пример 6. Найти минимальные ДНФ и КНФ:
f = (0, 1, 2, 4, 5, 7, 9, 12).
Решение. Если начать минимизацию с простой импликанты
AC
, то минимальную форму не получим, так как конъюнкция
AC
в минимальную ДНФ не входит (рис. 19). Для данной
функции существуют только одна минимальная ДНФ:
.
f
BCD
ABD
BCD
ABD
=
+
+
+
Рис. 19
1
1
1
1
1
1
1
1
Рис. 20
1
1
1
1
1
1
1
1
Ее КНФ существует также только одна (рис. 20):
.
f
BCD
ABD
BCD
ABD
=
+
+
+
(
)(
)(
)(
).
f
B
C
D A
B
D B
C
D A
B
D
=
+ +
+ +
+ +
+ +
3.2 Тема 3: «Минимизация ДНФ с учетом
доопределения»
Эта работа выполняется так же, как и предыдущая. Особен-
ность ее состоит только в выборе такого доопределения задан-
ной функции, при котором получается выражение, содержащее
28
наименьшее число вхождений переменных по сравнению с лю-
быми другими способами доопределения. В данном подразделе
представлено несколько примеров минимизации булевых функ-
ций в классе дизъюнктивных нормальных форм.
Пример 1. Найти минимальную ДНФ с учетом неопреде-
ленных состояний:
f = (2, 7, 10, 13, 15).
[0, 5, 8, 11, 14].
Решение. В круглых скобках перечислены номера минтермов,
образующих заданную функцию четырех переменных. В квадрат-
ных скобках указаны неопределенные состояния. Нанесем функ-
цию на карту Вейча. На ней же отметим крестиками неопределен-
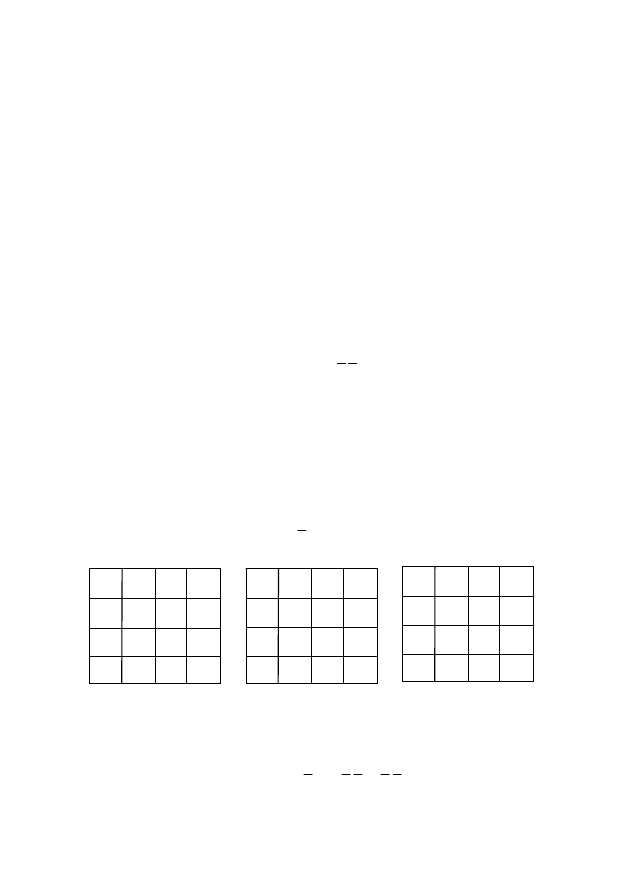
ные состояния (рис. 21). Если на этой карте на неопределенных
состояниях 11 и 14 поставить нули, а остальные крестики заменить
единицами, то получим искомую минимальную ДНФ:
.
f
BD
BD
=
+
Пример 2. Найти минимальную ДНФ с учетом неопреде-
ленных состояний:
f = (1, 2, 6, 7, 10, 13, 15). [0, 3, 4, 5, 8, 11, 12, 14].
Решение. Нанесем функцию на карту Вейча (рис. 22). Если
на неопределенном состоянии 8 принять значение функции,
равное нулю, а на всех остальных — единице, то минимальная
ДНФ примет вид:
.
f
A
B
C
= + +
×
Рис. 22
1
1
1
1
1
1
1
Рис. 21
1
1
1
1
1
×
×
×
×
×
Рис. 23
1
1
1
1
1
1
×
×
×
×
×
×
×
×
×
×
×
×
×
Пример 3. Карта Вейча приведена на рис. 23.
f = (1, 2, 6, 10, 13, 15). [0, 3, 4, 5,11, 12].
.
f
ABD
BC
AD
AC
=
+
+
+
29
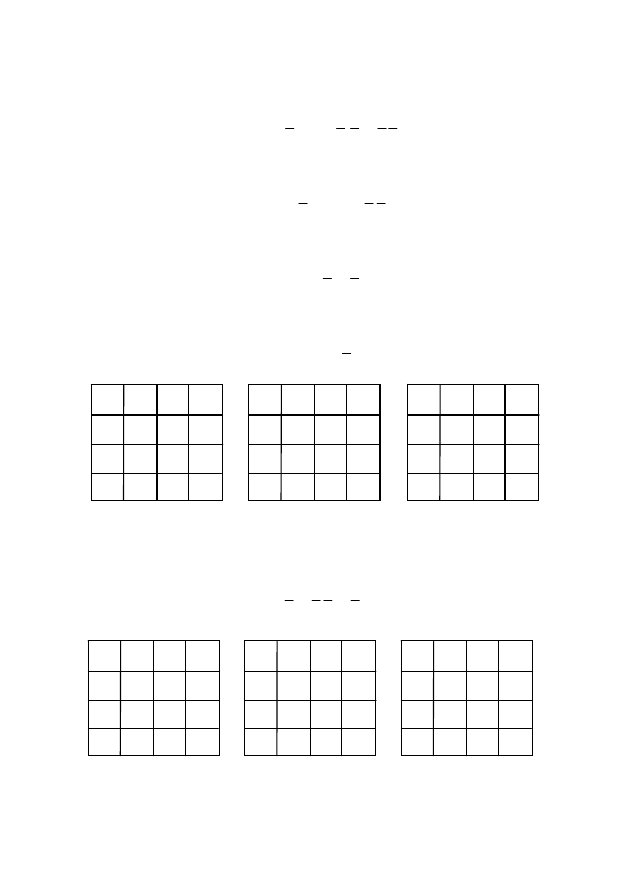
Пример 4. Карта Вейча приведена на рис. 24.
f = (1, 2, 4, 10, 11, 13, 15). [3, 7, 12, 14].
.
f
AB
BC
BC D
ABD
=
+
+
+
Пример 5. (Рис. 25).
f = (1, 2, 4, 6, 7, 8, 11, 14, 15).
[0, 5, 10, 12, 13].
.
f
B
D
AC
AC
= + +
+
Пример 6. (Рис. 26).
f = (1, 2, 4, 5, 6, 7, 10, 13, 15).
[3, 8, 12, 14].
.
f
B
CD
AD
= +
+
Пример 7. (Рис. 27).
f = (4, 5, 6, 7, 10, 12, 15).
[3, 8, 13, 14].
.
f
B
AD
= +
Рис. 24
1
1
1
1
1
1
1
Рис. 25
1
1
1
1
1
1
1
1
1
Рис. 26
1
1
1
1
1
1
1
1
1
×
×
×
×
×
×
×
×
×
×
×
×
×
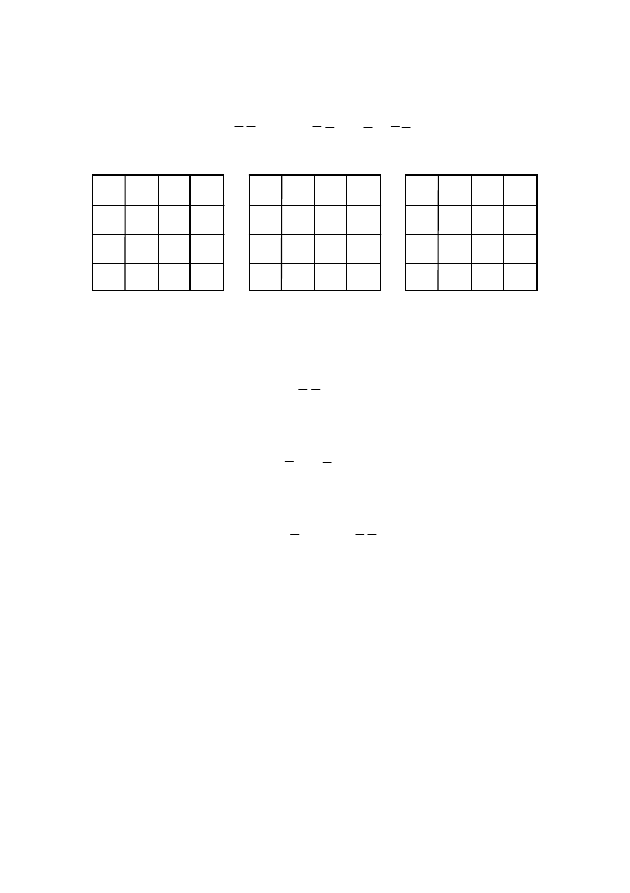
Пример 8. (Рис. 28).
f = (1, 2, 5, 6, 8, 9, 11, 12). [0, 3, 4, 13, 14].
.
f
C
AD
BD
= +
+
Рис. 27
1
1
1
1
1
1
1
Рис. 29
1
1
1
1
1
1
1
1
1
Рис. 28
1
1
1
1
1
1
1
1
×
×
×
×
×
×
×
×
×
×
×
×
30
Пример 9. (Рис. 29).
f = (0, 1, 3, 4, 5, 6, 8, 10, 15).
[11, 12, 14].
.
f
AC
AC
C D
BD
ABD
=
+
+
+
+
Рис. 30
1
1
1
1
1
Рис. 32
1
1
1
1
1
1
1
1
1
Рис. 31
1
1
1
1
1
1
1
1
×
×
×
×
×
×
×
×
×
×
×
×
1
×
Пример 10. (Рис. 30).
f = (0, 4, 5, 7, 12, 15).
[3, 8, 13, 14].
.
f
C D
BD
=
+
Пример 11. (Рис. 31).
f = (1, 5, 6, 8, 9, 11, 12, 15).
[0, 3, 4, 13, 14].
.
f
C
BD
AD
= +
+
Пример 12. (Рис. 32).
f = (0, 1, 3, 4, 5, 8, 9, 10, 15). [7, 11, 12, 14].
.
f
AB
CD
AC
=
+
+
3.3 Тема 4: «Минимизация КНФ с учетом
доопределения»
Нахождение минимальных КНФ с учетом неопределенных
состояний осуществляется следующим образом:
1) наносим заданную функцию на карту Вейча;
2) на ней же отмечаем неопределенные состояния. Если в
какой-либо клетке встретятся крестик и единица, то ставим кре-
стик;
3) строим карту для инверсии заданной функции. Заметим,
что инвертируются только нули и единицы, а все крестики (т.е.
неопределенные состояния) остаются на прежних местах;