ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 5652
Скачиваний: 10

86
4.2.1 Базы вершин. Ядра
Множество
X
Z
∈ называется базой вершин орграфа
L=(X,U,P), если
{
}
z Z
Д Z
X
u
z z
Z z
z
z
Д Z
Д Z
Y Y
Д Z Y
∈
∪
=
∨
∈
+ → ∉
=
⊂
( )
[
( )]
( )
/
( , )
1 2
1
2
1
т.е. множество L вершин, достижимых из вершины Z. Иными
словами, всякая из вершин достижима хотя бы из одной вершины
Z множества X, но различные вершины множества Z недостижи-
мы друг из друга.
Бикомпоненту L
i
=(X
i
,U
i
,P) орграфа L=(X,U,P) назовём базо-
вой, если в неё не заходит извне ни одна дуга.
Базовые бикомпоненты можно найти по «установившейся»
матрице (E+R)
lo
: её столбец отвечает вершине из базовой компо-
ненты тогда и только тогда, когда он не поглощает (при сложе-
нии) никакой другой столбец с меньшим числом единиц; иначе
−
если строка не поглощается никакой строкой с большим числом
единиц.
Лемма. Всякий орграф имеет по крайней мере одну базовую
компоненту.
Теорема. Множество
X
Z
∈ является базой вершин орграфа
тогда и только тогда, когда оно образовано вершинами, взятыми
по одной из каждой базовой бикомпоненты этого графа.
Следствие 1. Все базы вершин одного и того же орграфа
обладают одинаковым числом вершин.
Следствие 2. Для единственности базы вершин орграфа не-
обходимо и достаточно, чтобы каждая его базовая бикомпонента
была одновершинной.
Алгоритм нахождения баз вершин включает в себя выявле-
ние базовых бикомпонент графа.
Обозначим
Ξ отображение, относящее каждому не пустому
подмножеству
X
Y
∈ некоторое подмножество Ξ
X
Y
∈ , т.е.
X
Y
y
x
∈
∪
=
Ξ
.
,
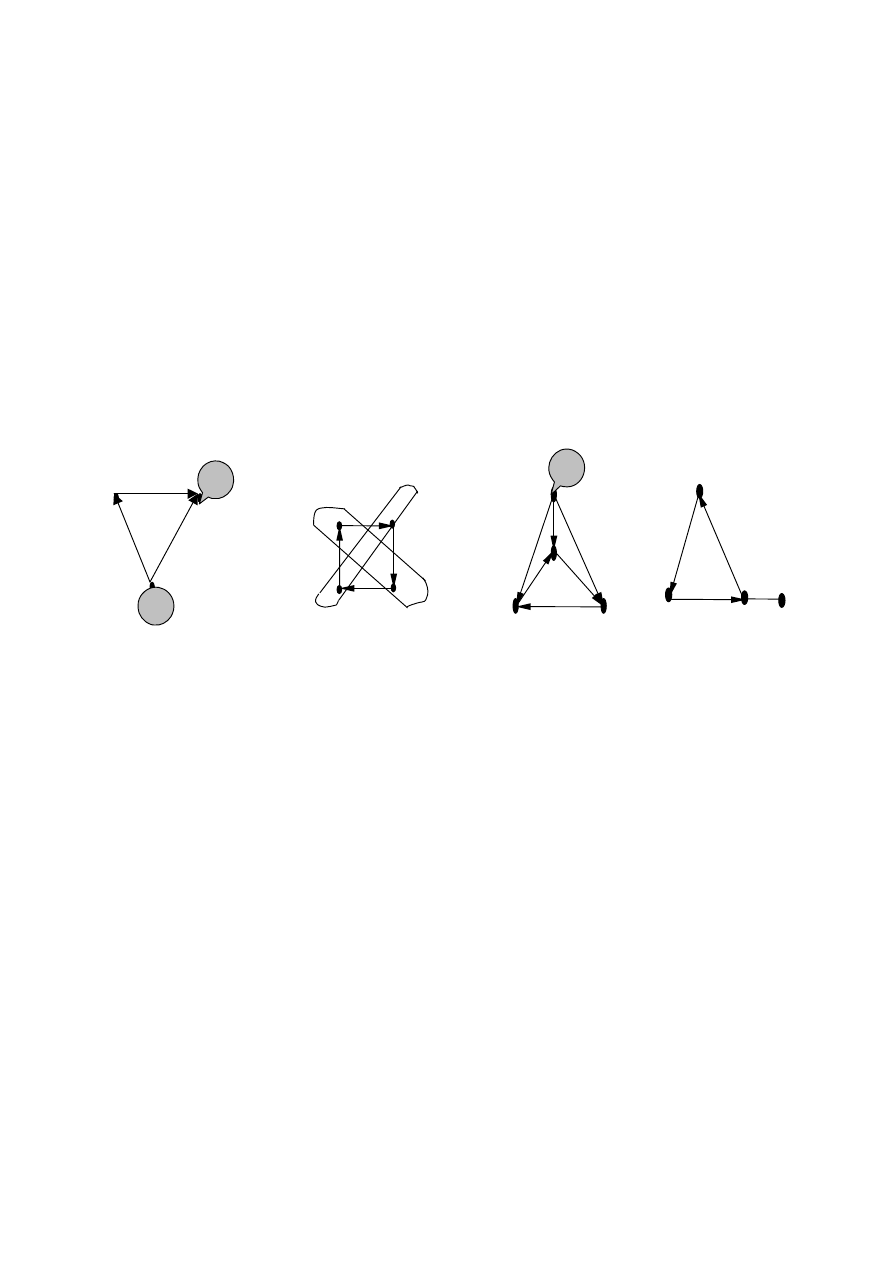
87
Множество
X
N
∈
+
называется положительным ядром орг-
рафа L, если
+
+
=
Ξ
N
X
N
\
; аналогично множество
X
N
∈
−
есть
отрицательное ядро, если
−
−
=
Ξ
N
X
N
\
.
Иначе, определения для N
+
и N
–
имеют вид:
)
(
\
&
)
(
1
∅
≠
∩
Γ
∈
∀
∅
=
∩
Γ
∈
∀
+
−
+
+
+
N
y
N
x
y
N
x
N
x
и
)
(
\
&
)
(
1
∅
=
Γ
∈
∀
∅
=
∩
Γ
∈
∀
−
−
−
−
−
N
y
N
x
y
N
x
N
x
Пример 4.2.3. Граф L
1
на рисунке 4.2.2 обладает как положи-
тельным, так и отрицательным ядром, граф L
2
− двумя ядрами, каж-
дое из которых одновременно и положительное, и отрицательное,
граф L
3
− положительным ядром, а граф L
4
не имеет ядер.
--
+
+
L
1
L
2
L
3
L
4
Рис. 4.2.2
Изменение ориентации всех дуг орграфа на противополож-
ную превращает все положительные ядра в отрицательные и на-
оборот.
Пример 4.2.4. Пусть Х множество решений, каждое из кото-
рых может быть принято в некоторой ситуации. Выбор одного из
этих решений поручен группе экспертов, каждый из которых
имеет своё мнение о взаимной предпочтительной в отношении
каждой пары решений. Считаем, что решение Х эффективно, но
предпочитается решению Y, если часть экспертов, считая Х лучше
Y, имеет возможность добиться того, чтобы угодная им точка
зрения одержала верх. Однако если другая часть экспертов (мо-
жет быть и частично совпадающая с первой) считает, что Y лучше
Z и может добиться принятия решения Y (т.е. Y эффективно пред-
почитается Z), то может быть, что Х эффективно не предпочита-
ется Z: отношение эффективного предпочтения не транзитивно.

88
Введём в рассмотрение граф Бержа с множеством вершин Х,
считая за Гх множество решений, эффективно предпочитаемых
решению Х.
Пусть N
–
− отрицательное ядро графа (если оно существует);
Он Нейман и Моргенштерн предполагают ограничиться рассмот-
рением решений, соответствующих вершинам из N
–.
В обоснова-
ние этого предложения заметим, что никакое решение из N
–
не
может эффективно предпочитаться какому-либо решению из N
–
,
а это обеспечивает известную сплочённость; с другой стороны,
любое решение
−
∈
N
X
x
\
− эффективно предпочитается некото-
рое решение из N
–
, в силу чего Х сразу отвергается.
4.2.2 Алгоритм Рудяну нахождения ядер графа
Алгоритм основан на следующей теореме.
Теорема.
Подмножество
X
N
∈
+
вершин
орграфа
L=(X,U,P) является его положительным ядром тогда и только то-
гда, когда выполняются следующие три условия:
1.
+
−
+
+
⊆
⊆
∉
N
E
N
E
2.
∅
=
Ξ
∩
+
E
N
3. множество N\E
+
есть положительное ядро подграфа
L’=(X’,U,P), где
)
(
\
©
+
+
Ξ
∪
=
E
E
X
X
.
Для отрицательных ядер справедлива двойственная теорема.
Здесь
{
}
∅
=
Γ
∈
=
−
x
X
x
X
E
&
\
− множество всех тупиков
графа L.
{
}
∅
=
Γ
∈
=
−
−
1
&
\
X
x
X
E
− множество всех анти-тупиков
L.
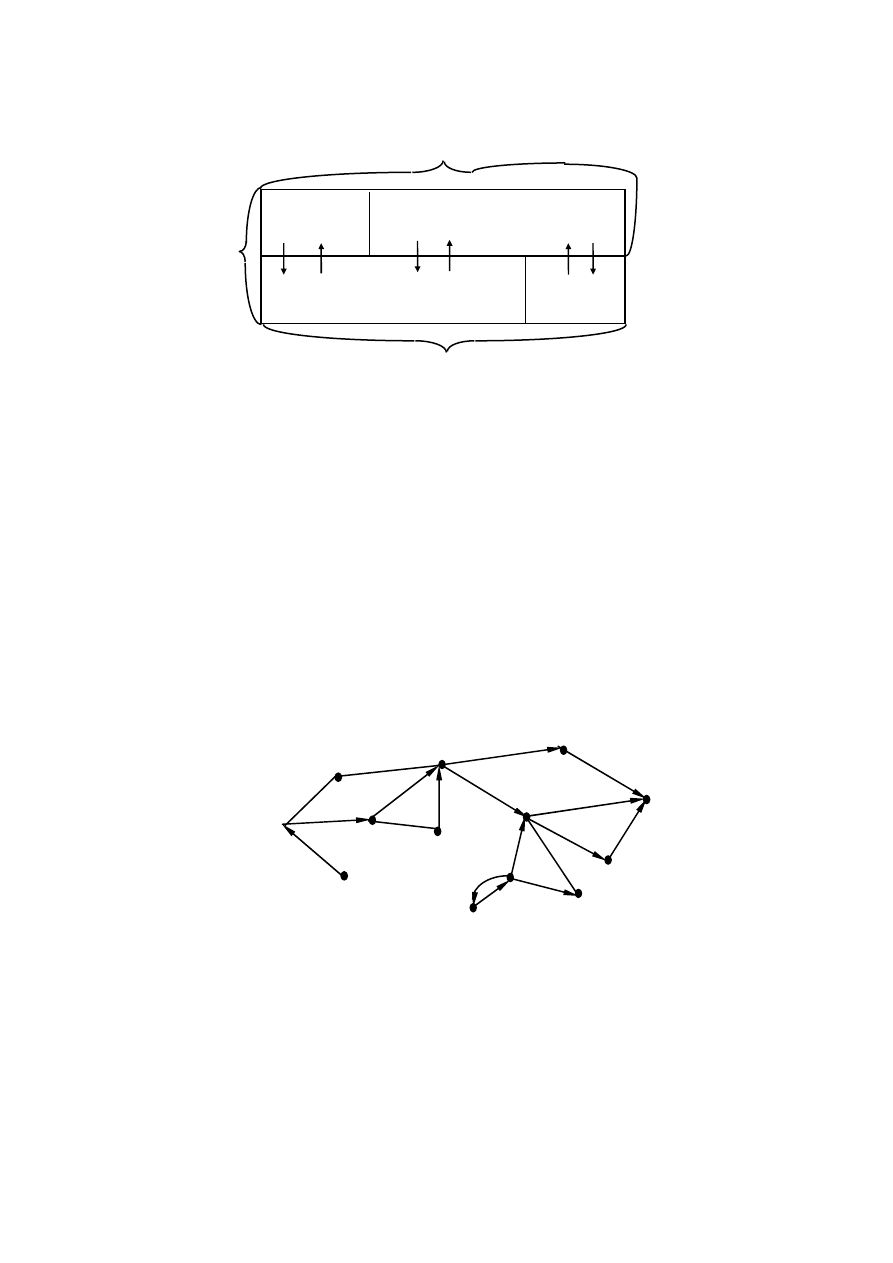
Доказательство. Пусть N-произвольное подмножество YX,
удовлетворяющее условиям 1 и 2, а N’=N\E
+
Ясно, что (рис. 4.2.3)
+
Ξ
∨
Ξ
=
Ξ
E
N
N
L
L
'
+
Ξ
Ξ
=
Ξ
E
N
N
L
L
\
'
'
89
Если N удовлетворяет, кроме 1 и 2, также условию 3, т.е.
N
X
N
L
′
′
=
′
Ξ
′
\
, то
N
X
E
N
X
E
N
N
L
L
L
\
)
\
(
=
Ξ
∨
′
′
=
Ξ
∨
′
Ξ
=
Ξ
+
+
′
,
а это означает, что N является положительным ядром графа L.
Наоборот, если N положительное ядро L, т.е.
L
X
N
\
=
Ξ
, то
условие
1
и
2,
очевидно
,
выполнены
,
поэтому
N
X
E
N
X
E
N
L
L
L
′
′
=
Ξ
=
Ξ
=
′
′
Ξ
+
+
\
\
)
\
(
,
иначе
N
−
положительное
ядро
L. При
∅
=
+
E
теорема
вырождается
в
тавтологию
.
Пример 4.2.5.
Найти
ядро
графа
,
изображённого
на
рисунке
4.2.4.
Рис. 4.2.4
Начнём
с
положительных
ядер
.
Прежде
всего
{ }
=
Ξ
Ξ
=
+
+
L
L
L
E
,
1
,
1
В
подграфе L’
,
полученном
из L
пополнением
вершин
4
и
11,
имеем
x'/N'
X'
Е'
N'
'
E
L
Ξ
N
Рис. 4.2.3
x/N
9
5
1
3
8
4
11
7
6
10
12
90
{ }
{ }
6
,
2
,
5
,
1
=
Ξ
=
+
′
′
+
′
L
L
L
E
E
.
Удаляя
из
L’
вершины
1,5,2
и
6,
получим
L’’
,
у
которого
{ }
{ }
8
,
3
=
Ξ
=
+
′′
′′
+
+
′′
L
L
L
E
E
.
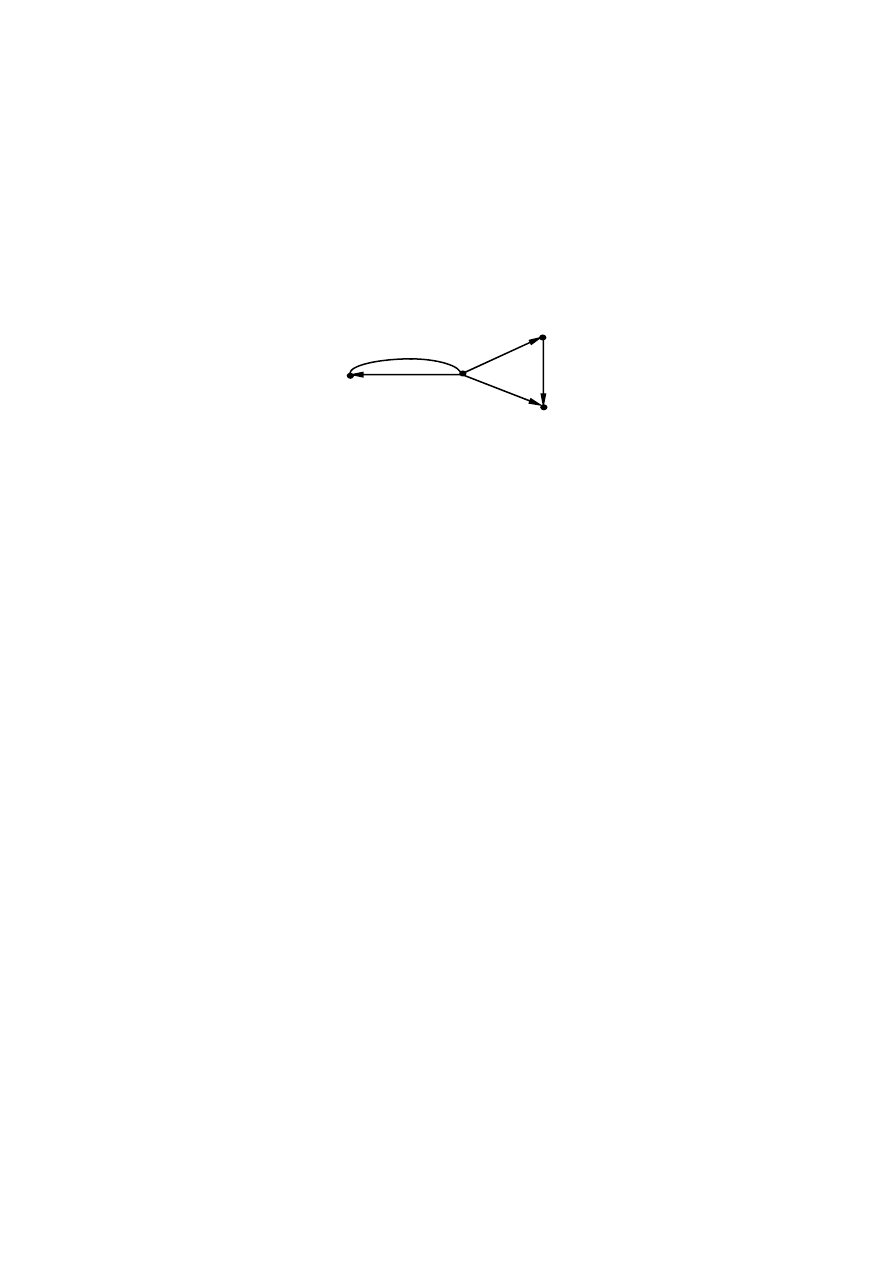
Наконец
,
удаление
из
L’’
вершин
3
и
8
даёт
граф
L’’
без
ан
-
титупиков
(
рис
. 4.2.5).
Рис. 4.2.5
Визуально
находим
в
L’’
два
положительных
ядра
: {9}
и
{7,12}.
Согласно
теореме
в L’’
положительными
ядрами
являются
{3,9}
и
{3,7,12},
в
L
− {1,3,5,9}
и
{1,3,5,7,12},
а
в
исходном
графе
L N
1
+
={1,3,5,9,11}
и
N
2
+
={1,3,5,7,11,12}.
Для
отрицательных
ядер
аналогично
имеем
}
10
,
7
,
3
{
};
8
{
=
Ξ
=
−
−
L
L
L
E
E
.
В
подграфе
L’
,
после
удаления
вершин
8,3,7,10:
}
6
,
5
,
1
{
},
2
{
1
=
Ξ
=
−
−
′
−
′
L
L
L
E
E
и
т
.
д
.
Окончательно
получим N
–
={2,4,8,12}.
7
12
10
9