ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 5656
Скачиваний: 10

76
вые рёбра; удалив любое из них, получим
L
’
с
( )
( ) ( )
=
′
=
′
L
L
L
λ
χ
χ
,
. Согласно предположению индукции мож-
но удалить рёбер так, чтобы остался граф
T
без циклов с
( )
( )
L
T
χ
χ
=
. Тот же
T
получен из исходного графа
L
удалением
1
+ ребра, причём
( )
( )
L
T
χ
χ
=
, что и требовалось доказать.
Второе утверждение справедливо потому, что при удалении
любого ребра
( )
L
λ
не может уменьшиться более чем на единицу.
Всякий суграф
T
графа
L
, удовлетворяющий условиям
( )
( ) ( )
L
L
m
T
m
λ
−
=
,
( )
( )
L
T
χ
χ
=
,
( )
0
=
T
λ
, называется каркасом
графа. Рёбра графа
L
, не принадлежащие его каркасу
T
, называ-
ются хордами каркаса
T
и
L
. Число рёбер каждого из каркасов
графа
L
называется рангом
( )
L
ρ
этого графа и обозначается че-
рез
( )
( ) ( ) ( ) ( )
L
L
n
L
L
m
L
χ
λ
ρ
−
=
−
=
.
Если граф связан, то всякий его каркас является деревом.
Теорема. Каковы бы ни были каркас
T
графа
(
)
ρ
,
,
u
x
L
=
и
хорда
U
этого каркаса, в
L
существует цикл, содержащий и не
содержащий других хорд каркаса
T
; причём этот цикл простой и
только один
.
Доказательство. Пусть
X
и
Y
вершины графа
L
, соединён-
ные ребром
U
, а
T
‘
− та компонента каркаса
T
, что содержит эти
вершины. Так как
T
‘
− дерево, то в нём имеется одна и только
одна простая цепь, соединяющая
X
с
Y,
и эта цепь вместе с реб-
ром
U
образует искомый цикл, который называется простым и
единственным.
Эта теорема позволяет получать одни каркасы из других.
Пусть
T
− искомый каркас
L
, а
U
− какая-то хорда этого каркаса
(не петля). Добавив в
T
ребро
U
, выявим цикл, содержащий
U
, и
исключим из него какое-то другое ребро (не
U
).
Таким образом можно получить все каркасы графа.
3.5.1 Алгоритм Степанеца, Влэдуца нахождения каркаса
графа
Алгоритм основан на использовании разметки вершин, при-
меняемой при нахождении кратчайшей цепи.
77
Произвольную вершину графа метим меткой 0, далее при-
сваиваем метку 1 всем вершинам, смежным с помеченными, и
т.д., пока все вершины не будут помечены. Если с, то повторяем
этот процесс для всех компонент.
Окончив разметку, просматриваем вершины графа и удаля-
ем рёбра по следующему правилу. Если мы находимся в вершине
X
с меткой
μ
, то удаляем рёбра, которые соединяют
X
с верши-
нами, имеющими метку
μ
, а из рёбер, соединяющих
X
с верши-
нами с меткой
μ
–1, сохраняем одно, удаляя все остальные.
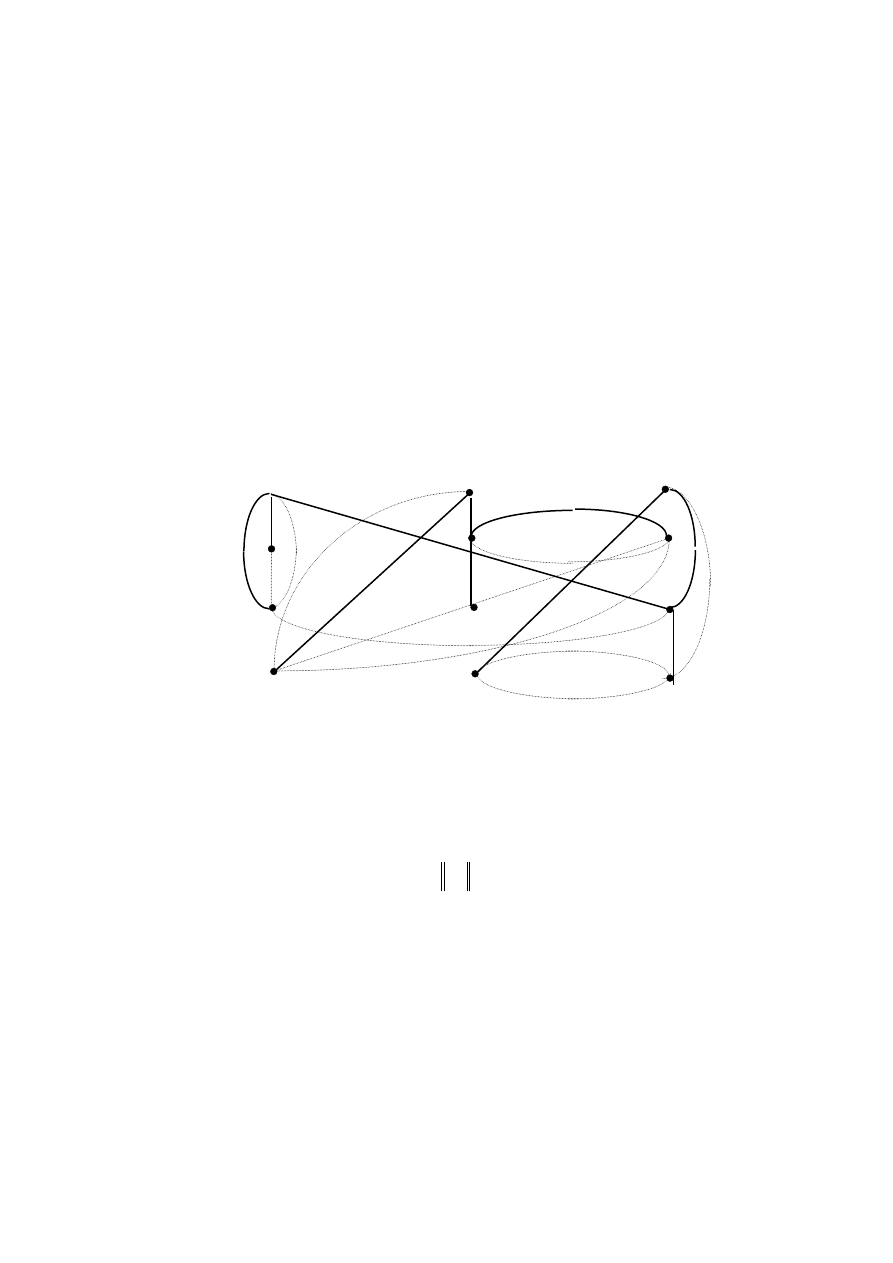
Пример 3.5.1. На примере графа на рисунке 3.4.1 рёбра кар-
каса
T
изображены жирными линиями; вершины просматрива-
лись в алфавитном порядке.
3.5.2 Анализ цикломатических свойств графа по матрице
инциденций
В матрице инциденций А=
ij
a
над свободным полукольцом,
где a
ij
– некоторые слова, построенные из элементов
,
,
,
,
θ
ς
η
ζ
со-
держится исчерпывающая информация о графе
(
)
ρ
,
,
u
x
L
=
. Од-
нако, так как нас при анализе цикломатических свойств графа не
интересуют ни ориентация, ни индивидуальность звеньев графа,
можно наложить следующие определяющие отношения:
0
,
0
,
1
=
=
η
ς
θ
η
ζ
.
d
(1)
q
(1)
a
(0)
b
(0)
c
(2)
e
(1)
f
(2)
i
(1)
h
(2)
j
(1)
k
(3)
l
(2)
Рис. 3.5.1
78
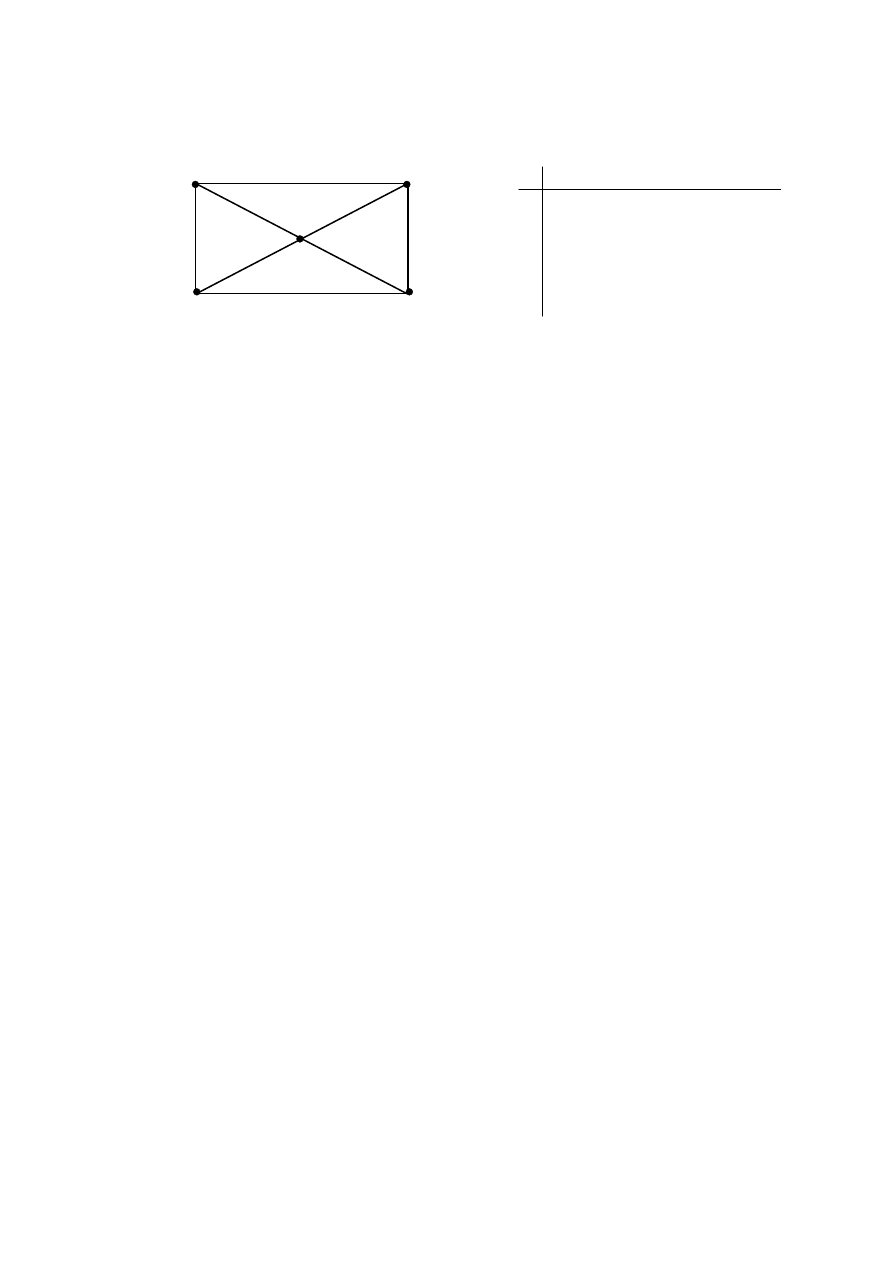
Пример 3.5.2.
a 2 b
5 6
1 3
8 7
4
d c
Теорема. Система
S
некоторых столбцов матрицы инциден-
ций A
L
графа
L
линейно независима тогда и только тогда, когда
суграф
T
S
, порождённый множеством тех рёбер графа
L
, которые
соответствуют столбцам
S
, не содержит циклов.
Следствие 1. Ранг
( )
L
A
ρ
матрицы инциденций A
L
равен
рангу графа
L.
Действительно, из графа
L
всегда можно удалить
( )
L
m
ρ
−
рёбер, чтобы оставшемуся суграфу
L’
отвечали линейно незави-
симые столбцы матрицы A
L
, поэтому
( )
( )
L
A
l
ρ
ρ
≥
. С другой сто-
роны, всякий суграф, получаемый из
L
удалением менее чем
( )
L
m
ρ
−
рёбер, обладает циклами, поэтому система более чем из
( )
L
ρ
столбцов матрицы A
L
всегда линейно зависима, откуда
( )
( )
L
A
ρ
ρ
≤
.
Следствие.
Система S из
( )
L
ρ
столбцов матрицы A
L
ли-
нейно независима тогда и только тогда, когда соответствующий
суграф
T
S
является каркасом графа
L
.
Действительно, высказывание о линейной независимости в
данном случае равносильно высказыванию
( )
( )
L
T
L
ρ
ρ
=
, т.е. вме-
сте с
( )
( )
L
T
m
S
ρ
=
, высказыванию
( ) ( ) ( )
( )
0
&
=
−
=
S
S
T
L
L
m
T
m
λ
λ
,
означающему, что
T
S
− каркас графа
L
.
3.5.3 Определение числа каркасов
Пусть дан граф
( )
L
x u
= , ,
ρ
, где
{
}
.
,
,
,
2
1
n
X
X
X
X
…
=
Образуем квадратную матрицу
1
1
1
1
0
0
0
0
1
0
0
0
1
0
0
1
0
1
0
0
1
1
0
0
0
0
1
0
0
1
1
0
0
0
0
1
0
0
1
1
8
7
6
5
4
3
2
1
e
d
c
b
a
A
L
=

79
2S(X
1
)-V(X
1
)-S(X
1
X
2
)- ....-S(X
1
X
n
)
Sn=
S
ij
= -S(X
1
X
2
)+2S(X
2
)-V(X
2
) - .... - S(X
2
X
n
) ,
........ ......... ........
-S(X
n
X
2
)-S(X
n
X
2
) - .... - 2S(X
n
)-V(X
n
)
в которой каждый диагональный элемент S
ij
выражает количество
петель графа
L
, инцидентных вершине
X
i
, а элемент S
ij
при
j
i
≠
равен взятому со знаком минус числу рёбер, соединяющих вер-
шины
X
i
и
X
j
.
Теорема Лантьера
−
Трента. Пусть
Δ − некоторый глав-
ный минор порядка
( )
L
ρ
ρ
=
матрицы S
L
, полученный вычёрки-
ванием
( )
L
χ
строк и такого же количества одноимённых столб-
цов. Если вычеркнутые ряды соответствуют вершинам графа
L
,
взятым по одной из каждой его компоненты связности, то
Δ ра-
вен числу различных каркасов графа
L
; в остальных случаях
Δ =0.
Если граф
L
связан, то
( )
1
−
=
n
L
ρ
и искомое число каркасов
равно любому из главных миноров n–1-го порядка матрицы S
L
(т.е. вычеркнуты можгут быть любая строка и столбец матрицы
S
L
).
80
4
ОРИЕНТИРОВАННЫЕ
ГРАФЫ
4.1
Маршруты
на
ориентированном
графе
Если в определении маршрута
X
0
U
1
X
1
U
2
X
2
...X
l–1
U
l
X
l
графа
(
)
ρ
,
,
u
x
L
=
заменить требование истинности высказывания
)
,
,
(
~
&
&
)
,
,
(
~
&
)
,
,
(
~
1
2
2
1
1
1
0
l
l
l
X
U
X
P
X
U
X
P
X
U
X
т
−
…
более жёст-
ким требованием истинности
…
&
)
,
,
(
&
)
,
,
(
2
2
1
1
1
0
X
U
X
P
X
U
X
т
)
,
,
(
&
1
l
l
l
X
U
X
P
−
, то получится определение
частично ориенти-
рованного маршрута из вершины Х
0
в вершину Х
L
; понятия час-
тично ориентируемого цикла возникают автоматически.
Требуя, чтобы все рёбра частично ориентированного мар-
шрута были дугами, приходим к понятиям ормаршрута
,
орцепи
и орцикла
.
Путём называется частично ориентированная цепь, не
содержащая звеньев.
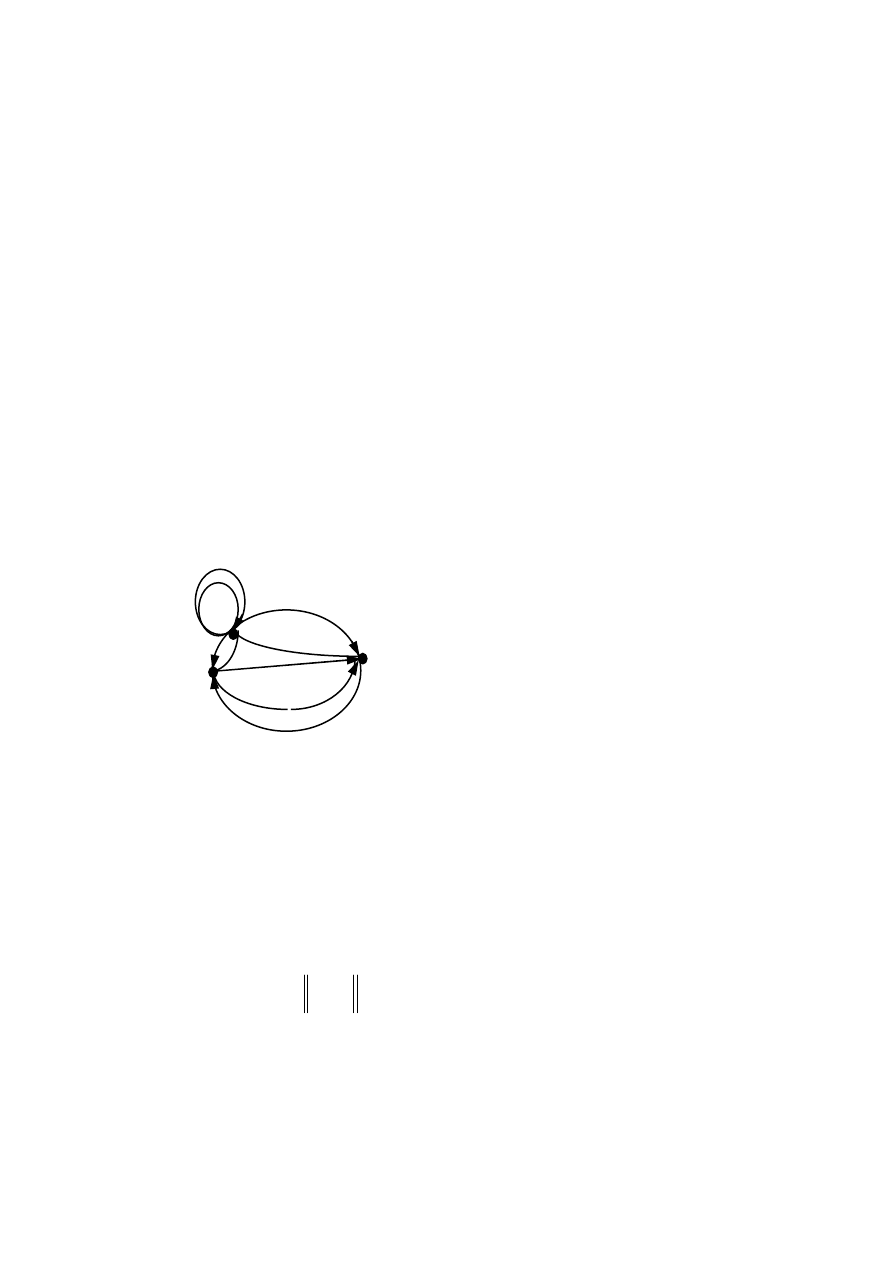
Пример 4.1.1. В графе на рисунке.4.1.1 маршруты а
1
а
4
в
9
с
1
а
3
в
9
с
6
а
(циклический) являются
частично ориентированными, но
не маршрутами, а в
9
с
8
в
9
с
(цик-
лический) суть ормаршрут; мар-
шрут
а
3
в
9
с
8
в есть
орцепь (не про-
стая), а
а
3
в
9
с
6
–простая орцепь;
маршрут в
9
с
8
в
–
простой орцикл.
Рис. 4.1.1
Для нахождения количества частично ориентированных
маршрутов заданной длины
l
из i-ой в j-ую вершину графа
L
по
его матрице смежности
R
достаточно на образующие полукольца
K
наложить соотношения
1
;
0
2
2
=
Θ
=
=
=
η
ξη
ηξ
,
тогда искомое количество маршрутов будет равно элементу
)
(
ij
r
матрицы
)
(e
ij
e
r
R
=
.
Аналогично подсчитываются маршруты, если К
подчинить
условиям
1
;
0
2
=
=
Θ
=
=
ξη
η
ηξ
,
6
8
4
2
3
1
a
b
5
1