Файл: Дискретная_мат._пос.pdf

 116 
 

Вариант 10 

1. Построить таблицу истинности для формулы:

.

)

(

&

B

B

A

A

F

→

→

=

2.  В  формуле 

)

~

(

)

~

(

1

Z

X

Z

Y

X

F

¬

∨

→

=

  избавиться  от  знаков  им-

пликации  и  эквиваленции.  С  помощью  равносильных  преобразований  убе-
диться,  что  она  равносильна  формуле 

Z

Y

X

F

¬

∨

∨

¬

=

2

.  Перечислить  ис-

пользуемые законы. 

3. Проверить правильность логического рассуждения сокращенным  спо-

собом. Какими другими способами можно решить эту задачу? 

“Если студент много занимается, то он успешно сдает экзамены. Студент 

не сдал экзамены. Следовательно, он занимался мало”. 

4. Используя два предиката, запишите предложение в виде формулы ло-

гики предикатов: “Некоторые певицы умеют танцевать”. Поставьте знак отри-
цания перед полученной формулой и приведите ее к предваренной нормальной 
форме.  

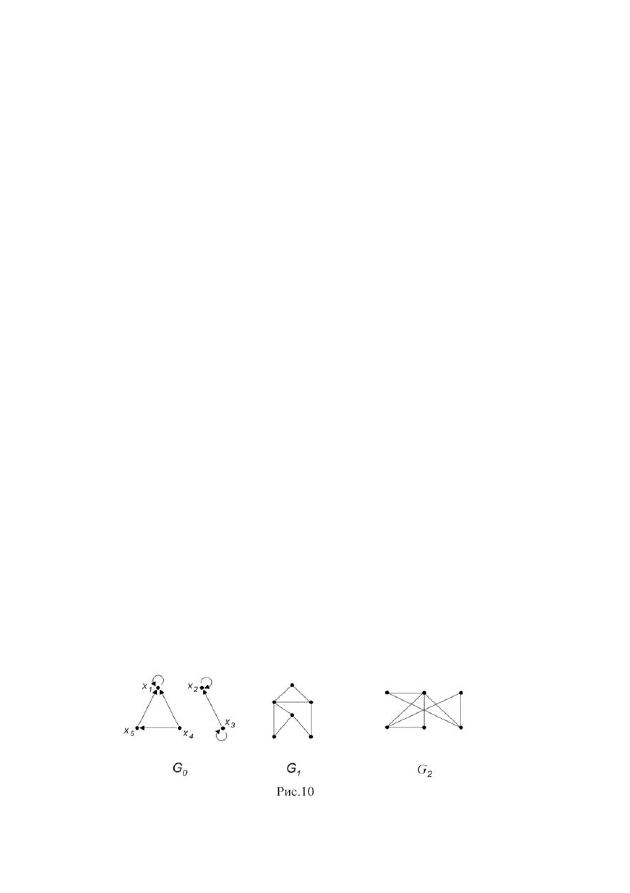
5. Для орграфа 

0

G

(рис. 10) найдите множество достижимости и множе-

ство контрдостижимости вершины 

1

x

. Выясните, какими свойствами обладает 

бинарное отношение, заданное графом 

0

G

.  Постройте  матрицу  смежности  и 

матрицу инцидентности, занумеровав дуги орграфа 

0

G

. 

6.  Занумеруйте  вершины  графа 

1

G

  (рис. 10) и  определите  степени  всех 

его  вершин.  Нарисуйте  какой-либо  остовный  подграф  графа 

1

G

.  Запишите 

матрицы смежности и инцидентности графа 

1

G

, занумеровав его ребра. 

7. Покажите, что графы 

1

G

 и 

2

G

 (рис. 10) изоморфны. Является ли граф 

2

G

 планарным? 

8.  Определите  цикломатическое  число  графа 

1

G

  (рис. 10). Выясните, 

можно ли нарисовать граф 

1

G

, не отрывая руки от бумаги и не проходя ни по 

одному ребру дважды. Ответ обоснуйте. 

9. Выясните, сколько ребер нужно удалить из графа 

1

G

 (рис. 10) при по-

строении  его  каркаса.  Занумеруйте  вершины  графа 

1

G

  и  постройте  каркас 

двумя способами (обход “в ширину”, обход “в глубину”), начав обход из вер-
шины с максимальной степенью.