Файл: Дискретная_мат._пос.pdf

 111 
 

Вариант 5 

1. Построить таблицу истинности для формулы: 
    

A

A

B

B

A

F

∨

¬

→

=

)

&

(

~

)

(

. 

2.  С  помощью  равносильных  преобразований  убедиться,  что  формулы 

X

Y

X

F

→

=

)

~

(

1

  и 

Y

X

F

∨

=

2

равносильны.  Перечислить  используемые 

законы. 

3. Проверить правильность логического рассуждения сокращенным  спо-

собом. Какими другими способами можно решить эту задачу? 

“Если цены высоки, то и зарплата высока. Цены высоки или применяется 

регулирование  цен.  Если  применяется  регулирование  цен,  то  нет  инфляции. 
Наблюдается инфляция. Следовательно, зарплата высока”. 

4. Используя два предиката, запишите предложение в виде формулы ло-

гики  предикатов: “Все  мыши  любят  сыр”.  Запишите  отрицание  полученной 
формулы и приведите ее к предваренной нормальной форме. 

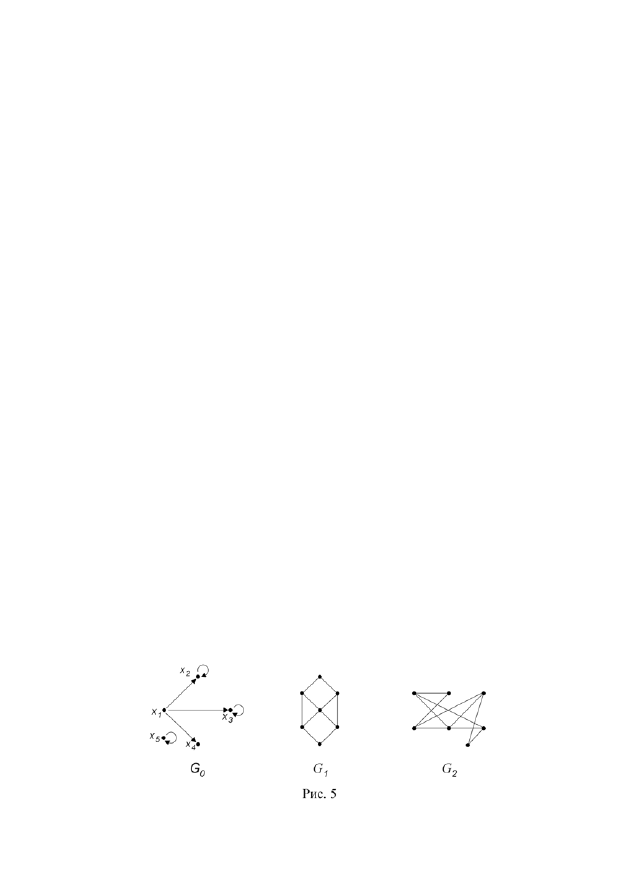
5.  Для  орграфа 

0

G

(рис. 5) найдите  множество  достижимости  и  множе-

ство контрдостижимости вершины 

1

x

. Выясните, какими свойствами обладает 

бинарное отношение, заданное графом 

0

G

.  Постройте  матрицу  смежности  и 

матрицу инцидентности, занумеровав дуги орграфа 

0

G

. 

6.  Занумеруйте  вершины  графа 

1

G

  (рис. 5) и  определите  степени  всех 

его  вершин.  Нарисуйте  какой-либо  остовный  подграф  графа 

1

G

.  Запишите 

матрицы смежности и  инцидентности графа 

1

G

, занумеровав его ребра. 

7. Покажите, что графы 

1

G

 и 

2

G

 (рис. 5) изоморфны. Является ли граф 

2

G

 планарным? 

8.  Определите  цикломатическое  число  графа 

1

G

  (рис. 5). Выясните, 

можно ли нарисовать граф 

1

G

, не отрывая руки от бумаги и не проходя ни по 

одному ребру дважды. Ответ обоснуйте. 

9. Выясните, сколько ребер нужно удалить из графа 

1

G

 (рис. 5) при по-

строении  его  каркаса.  Занумеруйте  вершины  графа 

1

G

  и  постройте  каркас 

двумя способами (обход “в ширину”, обход “в глубину”), начав обход из вер-
шины с максимальной степенью. 

 112 
 

Вариант 6 

1. Определить с помощью таблицы истинности, равносильны  ли форму-

лы: 

B

B

A

A

F

→

¬

∨

=

)

(

&

1

и 

B

A

F

→

=

2

. 

2.  С  помощью  равносильных  преобразований  убедиться,  что  формула 

A

A

B

A

F

~

)

(

&

1

→

=

  является  тавтологией.  Перечислить  используемые 

законы. 

3. Проверить правильность логического рассуждения сокращенным  спо-

собом. Какими другими способами можно решить эту задачу? 

“Либо аудитория была закрыта, либо, если преподаватель опоздал, то все 

студенты ушли в столовую. Если аудитория не была закрыта, то преподаватель 
не  опоздал.  Если  все  студенты  ушли  в  столовую,  то  преподаватель  опоздал. 
Следовательно, аудитория не была закрыта”. 

4. Используя два предиката, запишите предложение в виде формулы ло-

гики предикатов: “Некоторые петухи гордятся своим хвостом”. Поставьте знак 
отрицания  перед  полученной  формулой  и  приведите  ее  к  предваренной  нор-
мальной форме. 

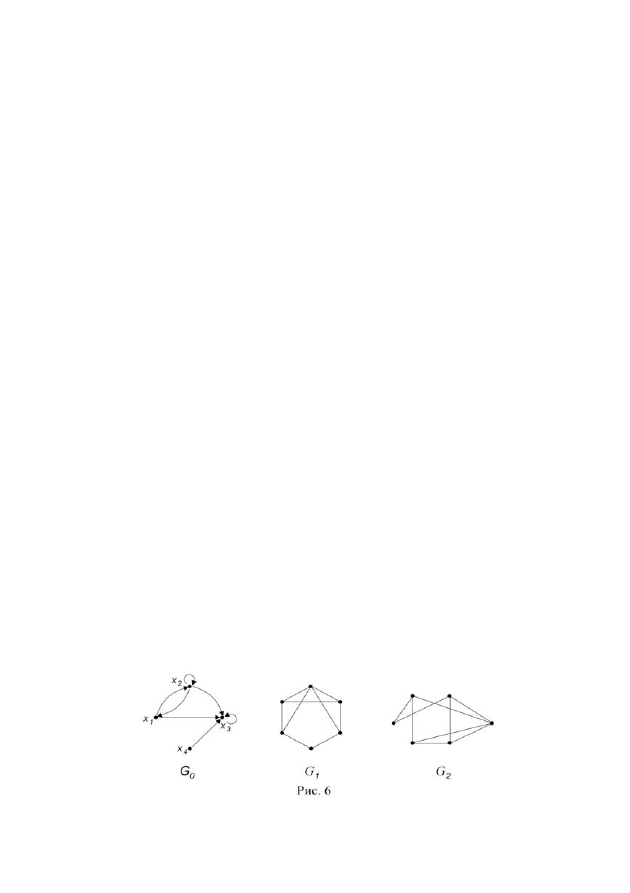
5.  Для  орграфа 

0

G

(рис. 6) найдите  множество  достижимости  и  множе-

ство контрдостижимости вершины 

1

x

. Выясните, какими свойствами обладает 

бинарное отношение, заданное графом 

0

G

.  Постройте  матрицу  смежности  и 

матрицу инцидентности, занумеровав дуги орграфа 

0

G

. 

6.  Занумеруйте  вершины  графа 

1

G

  (рис. 6) и  определите  степени  всех 

его  вершин.  Нарисуйте  какой-либо  остовный  подграф  графа 

1

G

.  Запишите 

матрицы смежности и инцидентности графа 

1

G

, занумеровав его ребра. 

7. Покажите, что графы 

1

G

 и 

2

G

 (рис. 2) изоморфны. Планарен ли 

2

G

? 

8.  Определите  цикломатическое  число  графа 

1

G

  (рис. 6). Выясните, 

можно ли нарисовать граф 

1

G

, не отрывая руки от бумаги и не проходя ни по 

одному ребру дважды. Ответ обоснуйте. 

9. Выясните, сколько ребер нужно удалить из графа 

1

G

 (рис. 6) при по-

строении  его  каркаса.  Занумеруйте  вершины  графа 

1

G

  и  постройте  каркас 

двумя способами (обход “в ширину”, обход “в глубину”), начав обход из вер-
шины с максимальной степенью.  

 113 
 

Вариант 7 

1. Построить таблицу истинности для формулы: 
    

A

A

B

A

F

¬

¬

¬

→

=

~

))

&

(

)

&

((

. 

2.  С  помощью  равносильных  преобразований  убедиться,  что  форму-

лы

))

(

&

(

&

1

C

B

B

B

A

F

∨

¬

¬

→

=

    и 

)

&

(

2

B

A

F

¬

=

равносильны.  Пере-

числить используемые законы. 

3. Проверить правильность логического рассуждения сокращенным  спо-

собом. Какими другими способами можно решить эту задачу? 

“Если  Павел  не  встречал  Ивана,  то  либо  Иван  не  был  на  лекциях,  либо 

Павел  лжет.  Если  Иван  был  на  лекциях,  то  Павел  встречал  Ивана,  и  Сергей 
был в читальном зале после лекции. Если Сергей был в читальном зале после 
лекции,  то  либо  Павел  не  был  на  лекциях,  либо  Павел  лжет.  Следовательно, 
Иван не был на лекциях. ”. 

4. Используя два предиката, запишите предложение в виде формулы ло-

гики предикатов: “Все храбрецы достойны славы”. Поставьте знак отрицания 
перед  полученной формулой и приведите ее к ПНФ. 

5.  Для  орграфа 

0

G

(рис. 7) найдите  множество  достижимости  и  множе-

ство контрдостижимости вершины 

1

x

. Выясните, какими свойствами обладает 

бинарное отношение, заданное графом 

0

G

.  Постройте  матрицу  смежности  и 

матрицу инцидентности, занумеровав дуги орграфа 

0

G

. 

6.  Занумеруйте  вершины  графа 

1

G

  (рис. 7) и  определите  степени  всех 

его  вершин.  Нарисуйте  какой-либо  остовный  подграф  графа 

1

G

.  Запишите 

матрицы смежности и инцидентности графа 

1

G

, занумеровав его ребра. 

7. Покажите, что графы 

1

G

 и 

2

G

 (рис. 2) изоморфны. Планарен ли 

2

G

? 

8.  Определите  цикломатическое  число  графа 

1

G

  (рис. 7). Выясните, 

можно ли нарисовать граф 

1

G

, не отрывая руки от бумаги и не проходя ни по 

одному ребру дважды. Ответ обоснуйте. 

9. Выясните, сколько ребер нужно удалить из графа 

1

G

 (рис. 7) при по-

строении  его  каркаса.  Занумеруйте  вершины  графа 

1

G

  и  постройте  каркас 

двумя способами (обход “в ширину”, обход “в глубину”), начав обход из вер-
шины с максимальной степенью. 

 114 
 

Вариант 8 

1. Построить таблицу истинности для формулы:

A

B

A

B

F

¬

∨

→

=

~

)

(

. 

2.  В  формуле 

)

(

&

)

(

))

&

(

C

A

A

B

C

B

A

F

→

¬

→

∨

→

¬

=

  избавиться 

от операции импликации и упростить с помощью равносильных преобразова-
ний. Перечислить используемые законы. 

3. Проверить правильность логического рассуждения сокращенным  спо-

собом. Какими другими способами можно решить эту задачу? 

“Если я буду говорить правду, то меня прославит простой народ. Если я 

буду лгать, то меня прославят богатые и знатные. Но я должен говорить прав-
ду или лгать. Значит меня прославит простой народ или прославят богатые и 
знатные”. 

4. Используя два предиката, запишите предложение в виде формулы ло-

гики  предикатов: “Некоторые  почтальоны  не  любят  собак”.  Поставьте  знак 
отрицания  перед  полученной  формулой  и  приведите  ее  к  предваренной  нор-
мальной форме. 

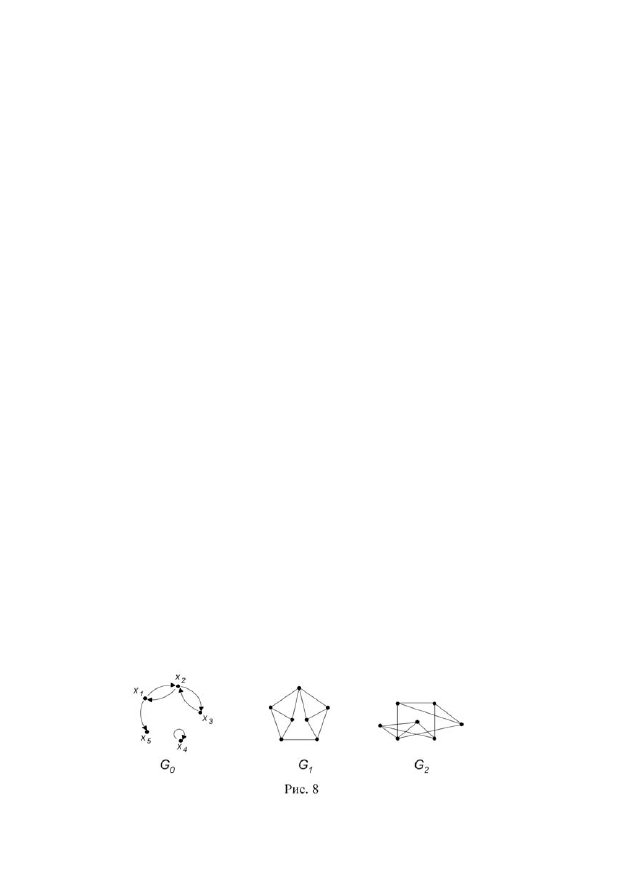
5.  Для  орграфа 

0

G

(рис. 8) найдите  множество  достижимости  и  множе-

ство контрдостижимости вершины 

1

x

. Выясните, какими свойствами обладает 

бинарное отношение, заданное графом 

0

G

.  Постройте  матрицу  смежности  и 

матрицу инцидентности, занумеровав дуги орграфа 

0

G

. 

6.  Дан  неорграф 

1

G

  (рис. 8). Занумеруйте  вершины  графа  и  определите 

степени всех его вершин. Нарисуйте какой-либо остовный подграф графа 

1

G

. 

Запишите матрицу смежности и матрицу инцидентности графа 

1

G

, занумеро-

вав его ребра. 

7. Покажите, что графы 

1

G

 и 

2

G

 (рис. 2) изоморфны. Планарен ли 

2

G

? 

8.  Определите  цикломатическое  число  графа 

1

G

  (рис. 8). Выясните, 

можно ли нарисовать граф 

1

G

, не отрывая руки от бумаги и не проходя ни по 

одному ребру дважды. Ответ обоснуйте. 

9. Выясните, сколько ребер нужно удалить из графа 

1

G

 (рис. 8) при по-

строении  его  каркаса.  Занумеруйте  вершины  графа 

1

G

  и  постройте  каркас 

двумя способами (обход “в ширину”, обход “в глубину”), начав обход из вер-
шины с максимальной степенью. 

 115 
 

Вариант 9 

1. Построить таблицу истинности для формулы: 

)

(

&

)

~

(

X

Y

Y

X

F

→

¬

=

. 

2.  С  помощью  равносильных  преобразований  убедиться,  что  формула 

B

A

A

B

A

F

∨

→

¬

→

¬

=

))

&

(

(

    является  тавтологией.  Перечислить  ис-

пользуемые законы. 

3. Проверить правильность логического рассуждения сокращенным  спо-

собом. Какими другими способами можно решить эту задачу? 

“Если ты будешь говорить правду, то тебя возненавидят богатые и знат-

ные. Если ты будешь лгать, то тебя возненавидит простой народ. Но ты дол-
жен говорить правду или лгать. Значит, тебя возненавидят богатые и знатные 
или тебя возненавидит простой народ ”. 

4. Используя два предиката, запишите предложение в виде формулы ло-

гики предикатов: “Все танцоры - стройные люди”. Поставьте знак отрицания 
перед полученной формулой и приведите ее к предваренной нормальной фор-
ме. 

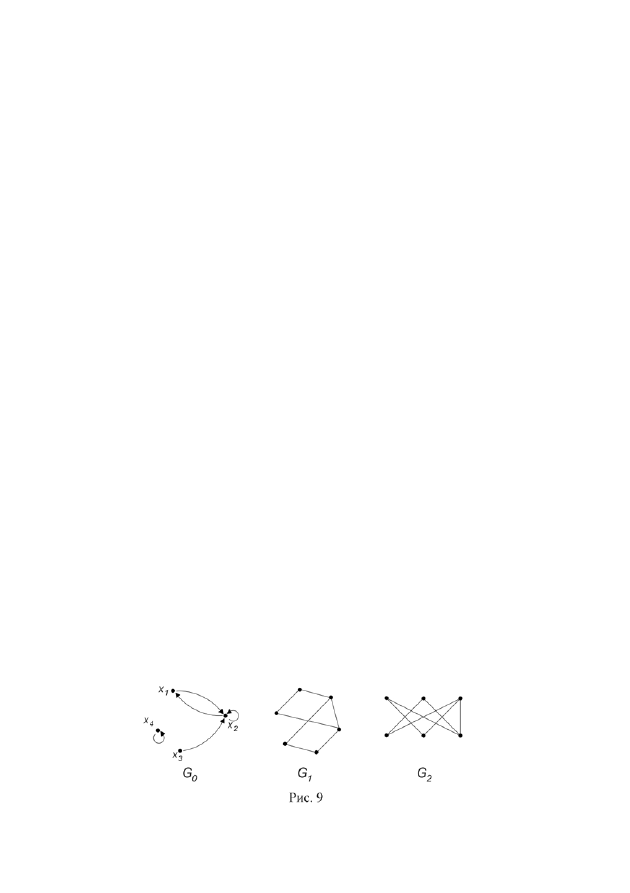
5.  Для  орграфа 

0

G

(рис. 9) найдите  множество  достижимости  и  множе-

ство контрдостижимости вершины 

1

x

. Выясните, какими свойствами обладает 

бинарное отношение, заданное графом 

0

G

.  Постройте  матрицу  смежности  и 

матрицу инцидентности, занумеровав дуги орграфа 

0

G

. 

6.  Занумеруйте  вершины  графа 

1

G

  (рис. 9) и  определите  степени  всех 

его  вершин.  Нарисуйте  какой-либо  остовный  подграф  графа 

1

G

.  Запишите 

матрицы смежности и инцидентности графа 

1

G

, занумеровав его ребра. 

7. Покажите, что графы 

1

G

 и 

2

G

 (рис. 2) изоморфны. Планарен ли 

2

G

? 

8.  Определите  цикломатическое  число  графа 

1

G

  (рис. 9). Выясните, 

можно ли нарисовать граф 

1

G

, не отрывая руки от бумаги и не проходя ни по 

одному ребру дважды. Ответ обоснуйте. 

9. Выясните, сколько ребер нужно удалить из графа 

1

G

 (рис. 9) при по-

строении  его  каркаса.  Занумеруйте  вершины  графа 

1

G

  и  постройте  каркас 

двумя способами (обход “в ширину”, обход “в глубину”), начав обход из вер-
шины с максимальной степенью.