ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 10266
Скачиваний: 94
6
1. ТЕОРИЯ МНОЖЕСТВ
1.1
Множества и операции над ними
1.1.1. Понятие множества
Теория множеств опирается на три первичных понятия:
1) множество;
2) элемент;
3) принадлежность.
Строгого определения этим понятиям не дается, описывается только их
применение.
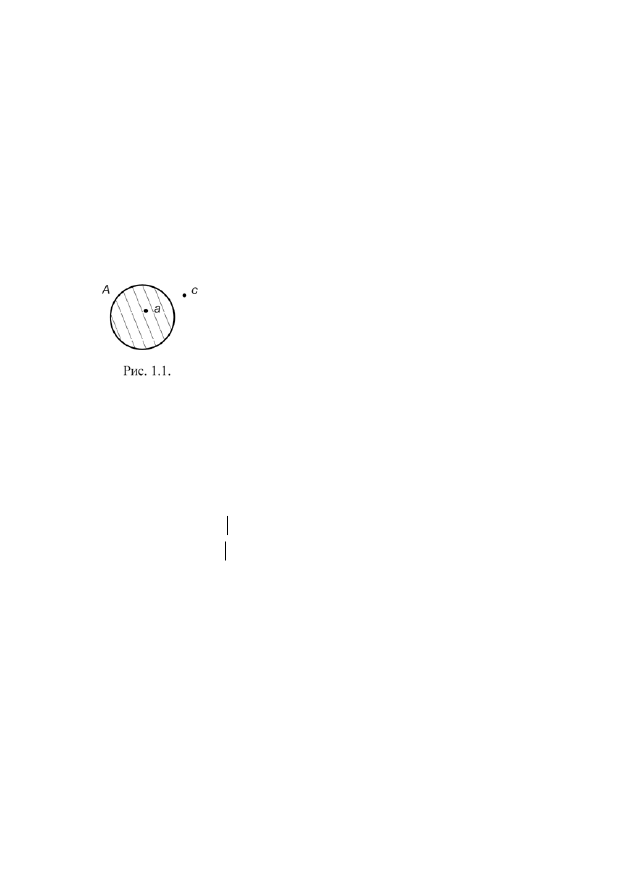
На рисунке 1.1 буквой
А
обозначено множество,
элементами которого являются точки заштрихованной
части плоскости, при этом точка а принадлежит множе-
ству
А
(
A
a
∈
), точка с не принадлежит множеству
А
(
A
c
∈
).
1.1.2. Способы задания множеств
Множество можно задать, перечислив все его элементы:
}
,
,
{
c
b
a
A
=
,
}
8
,
6
,
3
,
1
{
−
=
B
. Порядок записи элементов множества произволен. Часто за-
дают множество, указав его характеристическое свойство, которое для каждо-
го элемента позволяет выяснить, принадлежит он множеству или нет.
Например,
x
x
B
{
=
– целый корень уравнения
}
0
1
2
2
3
=
+
− x
x
,
x
,
7
x
1
x
{
C
≤
≤
−
=
– целое }.
В дальнейшем для известных числовых множеств будут использоваться
обозначения:
Ν
= { 1,2,3,…} – множество натуральных чисел;
Z
= { …, -2,-1,0,1,2,…} – множество целых чисел;
Q
– множество рациональных чисел;
R
– множество действительных чисел.
1.1.3. Основные определения
Пустым множеством называется множество
∅
, не содержащее ни одно-
го элемента, т.е. для любого элемента x выполняется
∉
x
∅
.
Универсальным называется множество U всех элементов, рассматривае-
мых в данной задаче.

7
Пример. Пусть U =
Z
и требуется найти все решения уравнения
2
2
=
x
.
Множество М решений этой задачи есть пустое множество: М =
∅.
Пусть теперь U =
R.
Тогда множество М решений уравнения
2
2
=
x
не
пусто: М =
}
2
,
2
{
−
.
Будем говорить, что множество
А
включается во множество
В
)
(
B
A
⊆
, если каждый элемент множества
А
является элементом множества
В
( говорят также, что
А
является подмножеством множества
В
). Из определе-
ния включения следуют свойства:
1)
A
A
⊆
для любого множества
А
;
2)
Если
B
A
⊆
и
C
B
⊆
, то
C
A
⊆
;
3)
∅
A
⊆
для любого множества
А
;
4)
⊆
A
U для любого множества
А
.
Определим понятие равенства множеств:
А=В
тогда и только тогда, ко-
гда одновременно выполняются два включения
B
A
⊆
и
A
B
⊆
, т.е. каждый
элемент множества
А
является элементом множества
В
и каждый элемент
множества
В
является элементом множества
А
.
1.1.4. Диаграммы Эйлера – Венна
Эти диаграммы применяются для наглядного изображения множеств и
их взаимного расположения.
Универсальное множество U изоб-
ражается в виде прямоугольника, а про-
извольные множества – подмножест-ва
универсального – в виде кругов (рис.
1.2).
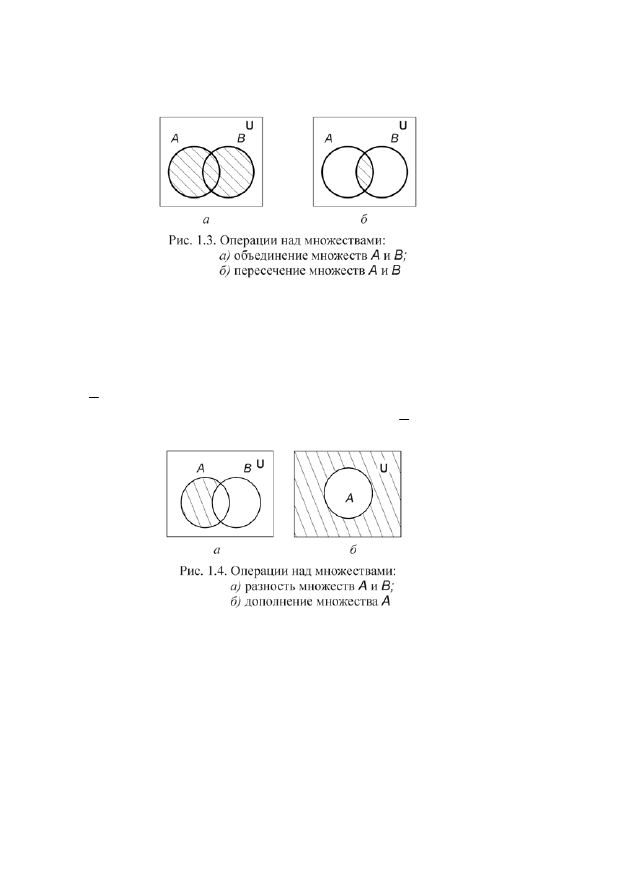
1.1.5. Операции над множествами
Объединением множеств
А
и
В
называется множество
B
A
∪
, состоя-
щее из тех и только тех элементов, которые принадлежат хотя бы одному из
множеств
А
или
В
(рис. 1.3, а).
Пример. Если
}
3
,
2
,
1
{
},
2
,
1
,
0
{
−
=
=
B
A
, то
}
3
,
2
,
1
,
0
,
1
{
−
=
∪ B
A
.
Пересечением множеств
А
и
В
называется множество
B
A
∩
, состоящее
из тех и только тех элементов, которые принадлежат одновременно и множе-
ству
А
, и множеству
В
(рис. 1.3, б).
8
Пример. Если
}
3
,
2
,
1
{
},
2
,
1
,
0
{
−
=
=
B
A
, то
}
2
{
=
∩ B
A
.
Разностью множеств
А
и
В
называется множество
B
A
\
тех и только
тех элементов, которые принадлежат множеству
А
и не принадлежат множе-
ству
В
(рис. 1.4, а).
Пример.
}
1
,
0
{
}
3
,
2
,
1
{
\
}
2
,
1
,
0
{
\
=
−
=
B
A
;
}
3
,
1
{
}
2
,
1
,
0
{
\
}
3
,
2
,
1
{
\
−
=
−
=
A
B
.
Дополнением множества
А
до универсального U называется множество
=
A
U
A
\
(рис. 1.4, б).
Пример. Если
}
2
,
1
,
0
{
=
A
, U
}
5
,
4
,
3
,
2
,
1
,
0
{
=
, то
=
A
U
}
5
,
4
,
3
{
\
=
A
.
1.1.6. Системы множеств
Элементы
множества
сами
могут
быть
множествами:
{
}
}
2
,
1
{
},
3
,
2
{
},
1
{
=
A
; в таком случае удобно говорить о системе множеств.
Рассмотрим такие системы множеств, как булеан и разбиение множеств.
Булеаном
B
(Х) множества
Х
называется множество всех подмножеств
множества
Х
. Например, для множества
}
1
,
0
{
=
X
булеаном является множе-
ство
B
{
=
)
(
X
∅
,
}
}
1
,
0
{
},
1
{
},
0
{
.

9
Разбиением
R
(Х) множества
Х
называется система его непустых непере-
секающихся подмножеств, в объединении дающая множество
Х
(рис. 1.5).
Например,
для
множества
}
5
,
4
,
3
,
2
,
1
{
=
X
можно построить разби-
ение
R
1
{
}
}
5
,
4
,
3
{
},
2
,
1
{
)
(
=
X
, состоящее
из двух элементов (они называются бло-
ками
разбиения),
или
разбиение
R
2
{
}
}
4
{
},
3
{
},
5
,
2
{
},
1
{
)
(
=
X
– из четы-
рех блоков; возможны и другие разбие-
ния этого множества
Х
.
1.1.7. Законы алгебры множеств
Так же, как операции обычной алгебры, операции над множествами вы-
полняются по законам (табл. 1.1), которые доказываются на основе введенных
выше определений. Особенностью алгебры множеств является закон идемпо-
тентности, благодаря которому в алгебре множеств нет числовых коэффици-
ентов и степеней.
Таблица 1.1
Законы алгебры множеств
№
Формулы
Название
1
A
∩
∅
=
∅
; A
∪
∅
= A; A
∩ A =
∅
Свойства пустого множе-
ства
2
A
∪U = U; A∩U = A; A∪Ā = U
Свойства универсального
множества
3
A
∩B = B∩A; A∪B = B∪A
Закон коммутативности
4
(А
∩В)∩С=А∩(В∩С);
(А
∪В)∪С=А∪(В∪С)
Закон ассоциативности
5
А
∩(В∪С)= (А∩В)∪(А∩С);
А
∪(В∩С)= (А∪В)∩(А∪С)
Закон дистрибутивности
6
А =А
Закон двойного дополне-
ния
7
А
∩А=А; А∪А=А
Законы идемпотентности
8
;
;
В
А
В
А
В
А
В
А
∪
=
∩
∩
=
∪
Законы де Моргана
9
А
∪(А∩В)=А; А∩(А∪В)=А
Законы поглощения

10
1.1.8. Решение задач 1-3 контрольной работы № 1
Задача 1. Решить задачу, пользуясь диаграммой Эйлера-Венна.
Группа туристов из 100 человек пробыла в городе N три дня. За это вре-
мя драматический театр посетили 28 туристов, оперный – 42, кукольный – 30.
И в драматическом, и в оперном побывало 10 человек; в драматическом и ку-
кольном – 8; в оперном и кукольном – 5. Все три театра посетили три челове-
ка. Сколько туристов не были ни в одном театре?
Решение. В задаче идет речь о трех множествах Д, О, К – зрителей дра-
мы, оперы и кукольного спектакля соответственно. Универсальное множество
U – это множество туристов группы. Используя обозначение
)
(
X
n
– количе-
ство элементов множества
Х
, запишем кратко условие задачи:
(
n
U
;
100
)
=
;
30
)
(
;
42
)
(
;
28
)
(
=
=
=
К
n
О
n
Д
n
;
5
)
(
;
8
)
(
;
10
)
(
=
∩
=
∩
=
∩
К
О
n
К
Д
n
О
Д
n
.
3
)
(
=
∩
∩
О
К
Д
n
В задаче требуется найти
))
(
\
(
)
(
К
О
Д
U
n
К
О
Д
n
∩
∩
=
∪
∪
.
Перенесем эти данные на диаграмму Эйлера-Венна. Разметку диаграммы
начинаем с множества
К
О
Д
∩
∩
– здесь три элемента. В множестве
О
Д
∩
- 10 элементов, но три из них уже учтены. Оставшиеся 7 элементов
проставляем на диаграмме и т.д.
Теперь на диаграмме (рис. 1.6) все элементы учтены ровно по одному ра-
зу, следовательно, количество туристов, которые побывали хотя бы в одном
театре, равно
.
80
20
2
3
5
30
7
13
)
(
=
+
+
+
+
+
+
=
∪
∪
К
О
Д
n
Количество туристов, не побывавших ни в одном театре
(
n
U
.
20
80
100
))
\(
=
−
=
∪
∪
К
О
Д
Ответ: не были ни в одном театре 20 человек.