Файл: Дискретная мат-ка_УП.pdf

51

Введем правила упрощенного написания формул. 
Прежде  всего,  определим  приоритетность  выполнения  опе-

раций.  Для  этого  разобьем  их  на  группы  и  запишем  в  порядке 
уменьшения приоритета. 

¬; 

∧

; 

∨

; 

⊕

; 

→

; ~; 

Если  перед  нами  формула,  то,  прежде  всего,  выполняются 

операции в скобках и операция отрицания, затем – конъюнкция. 
Операции дизъюнкция и дизъюнкция с исключением имеют оди-
наковый приоритет. Если необходимо какую-либо из них выпол-
нять первой, то надо уточнить, используя скобки. То же самое ка-
сается операций импликации и эквивалентности, которые имеют 
наиболее низкий приоритет. 

Для  упрощения  написания  можно  опускать  знак  конъюнк-

ции. 

И последнее. Символ отрицания можно помещать над пере-

менной, скобкой в виде черты. 

Пример: 
 
Рассмотрим  формулы  А  и  В.  Визуально  формулы  могут 

быть различны, но может оказаться, что для каждого набора зна-
чений переменных значения 

ложь

 и 

истина

 совпадают, тогда го-

ворят, что формулы А и В 

равносильны

, т.е. А=В; А = И – фор-

мула истинна, если через И обозначить формулу, которая всегда 
истинна.  А=Л – формула  всегда  ложна.  Необходимо  заметить, 
что под символом = понимается отношение равенства. 

5.1 

Тождества

в

алгебре

высказываний

 
Пусть формула 

А

 зависит от списка переменных 

х

1

, х

2

, …,х

k

. 

Формула 

А

  называется 

тавтологией

  (тождественно-истинной), 

если  при  любом  значении  переменных 

х

1

,  х

2

, …,х

k

  формула 

А

принимает значение истина. То есть, тождества – это такие фор-
мулы, которые обращаются в 

истину

 при любой комбинации пе-

ременных. Рассмотрим основные тождества (законы). 

1. 

Закон  тождества.

  Всякое  высказывание  является  логи-

ческим следствием самого себя: 

х→х 

.

a

)

b

a

(

),

a

c

)(

b

a

(

⊕

∨

∨

→

52

2.

 Закон противоречия

. Для всякого высказывания х невер-

но, что истинно само высказывание и его отрицание: 

 
 
3. 

Закон  исключенного  третьего

.  Для      каждого  высказы-

вания х истинно само высказывание или его отрицание: 

х

∨

¬х 

4. 

Закон двойного отрицания

. Каково бы ни было высказы-

вание х, отрицание его отрицания эквивалентно самому высказы-
ванию: 

¬¬х~х 

5.

  Истина  из  чего  угодно

.  Если 

х

  истина,  то  каково  бы  ни 

было у высказывание 

у→х

 – истина: 

х→ (у→х) 

6. 

Из ложного – что угодно

.  Если 

х

  истина,  то 

¬х

 – ложь. 

Ложь имплицирует все, что угодно: 

¬х→ (х→у) 

7. 

Modus ponens

 (правило отделения). Если 

х

 истина и 

х→у 

– 

истина, то 

у

 – истина: 

(х

∧

(х→у)) →у 

8. 

Modus tollens 

 (правило устранения). Если 

х

 имплицирует 

у

 и 

у

 ложно, то 

х

 ложно: 

((х→у) 

∧

¬у) →¬х 

9. 

Закон силлогизма

. Если из 

х

 следует 

у

 и из 

у

 следует 

z

, то 

из 

х

 следует 

z: 

(x→y) 

∧

 (y→z) → (x→z) 

10. 

Тривиальные тождества

: 

Л→А,       А→И. 

5.2 

Булевы

формулы

 
Булевыми  формулами  назовем  такие  формулы,  в  которых  

отсутствуют знаки операций 

→

; ~; 

⊕

.

 Рассмотрим основные рав-

носильности  булевых  формул.  Эти  равносильности  носят  назва-
ние законов. Доказательство законов можно провести с помощью 
таблиц  истинностей.  Пусть  А,  В  и  С – формулы.  Тогда  для  них 
справедливы следующие законы: 

)

x

x

(

),

x

x

(

¬

∧

¬

∧

53

1.

Коммутативные

: 

А

∨В = В∨А, 

А

∧В = В∧А. 

2.

Ассоциативные: 

А

∨ (В∨С) = (А∨В) ∨С, 

А

∧ (В∧С) = (А∧В) ∧С. 

3.

Идемпотентности

: 

А

∨А = А, 

А

∧А = А. 

4.

Дистрибутивные: 

(А

∨В)С = АС ∨ ВС, 

А

∨ВС = (А∨В)(А∨С). 

5.

Де Моргана: 

 
6.

Двойного отрицания: 

 
7.

 А 

∨ Ā = И,   А ∧ Ā = Л, 

  А 

∨ Л = А,   А ∧ Л = Л, 

    А 

∨ И = И,   А ∧ И = А. 

8. 

Л

И

,

И

Л

=

=

.

5.3 

Интерпретации

Определим  формальную  систему,  в  которой  заданы  пере-

менные 

a, b, c,…;

  операции  над  переменными 

∨

, 

∧

, ¬

;  правила 

построения правильных формул; для придания более общего ха-
рактера, заменим  

Л

  и 

И

  на 

0

  и 

1

.  В  результате  получим  булеву 

алгебру. 

Интерпретации: 
1.

Булева  алгебра  высказываний

.  Считается,  что 

a, b, c,… –

высказывания. Значения 

0

 и 

1

 кодируем значениями 

Л

 и 

И

. Опе-

рации рассматриваются как логические связки

 НЕ

, 

ИЛИ

, 

И

. 

.

B

A

AB

,

B

A

B

A

∨

=

∧

=

∨

.

A

A

=

54

2.

Булева алгебра множеств

. Считаем, что 

a, b, c,… –

 мно-

жества, 

0

  и 

1

  интерпретируются  как 

∅ и 

Т

,  а  операции:  как  до-

полнение 

¯

, объединение 

∪, пересечение ∩. 

3.

Булева  алгебра  событий

.  Переменные 

a, b, c,… –

  пред-

ставляют  события.  Событие  имеет  место  или  нет.  Несомненное 
событие обозначается 

1

.  Если  событие  не  наступило – 

0

.  Опера-

ции представляются символами 

∨

, 

∧

, 

¬

.

 Здесь 

¬ – отрицание со-

бытия, 

∨ – сумма событий, ∧ – произведение событий. Операци-

ям  придается  определенный  смысл.  Сумма  событий – это  собы-
тие, которое наступает, когда, по крайней мере, наступает одно из 
этих событий 

а

, 

b

. Произведение событий – событие, которое на-

ступает тогда, когда оба события имеют место. Алгебра событий 
является фундаментом теории вероятностей. 

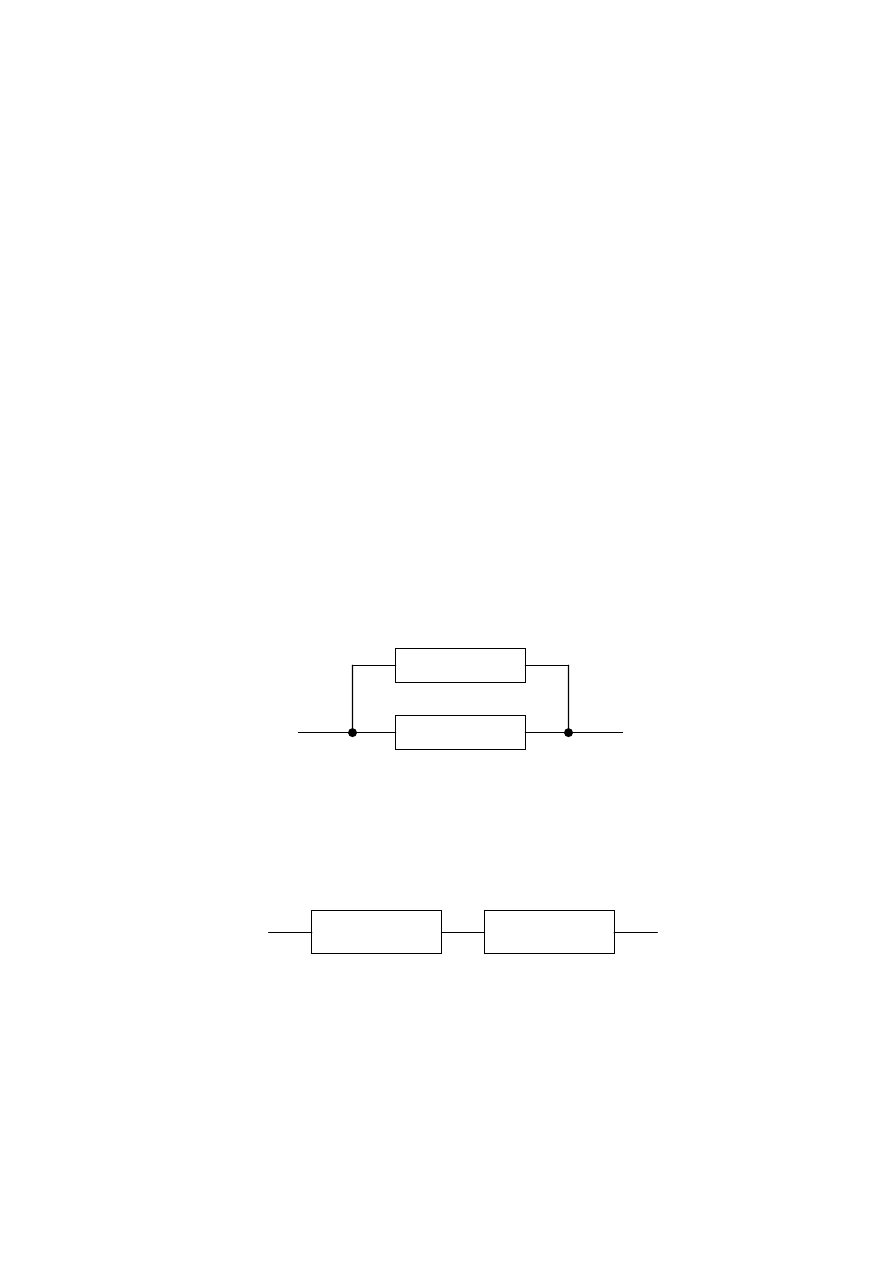
4.

Теория  электрических  цепей

.  Используются  те  же  самые 

булевы формулы. Переменные 

a, b, c,…

  ставятся  в  соответствие 

электрическим  цепям.  Интерпретация  рассматривается  с  точки 
зрения проводит цепь ток или нет. Цепь может находиться в двух 
состояниях: проводимом и не проводимом 
 

Рисунок  5.1 – дизъюнкция 

 
a

∨

b

 – означает  параллельное  соединение  двух  цепей,  ток 

проходит, если проводит a или b. 

Рисунок 5.2 –  Конъюнкция  

 
Последовательное соединение цепей –  

a 

∧

 b.

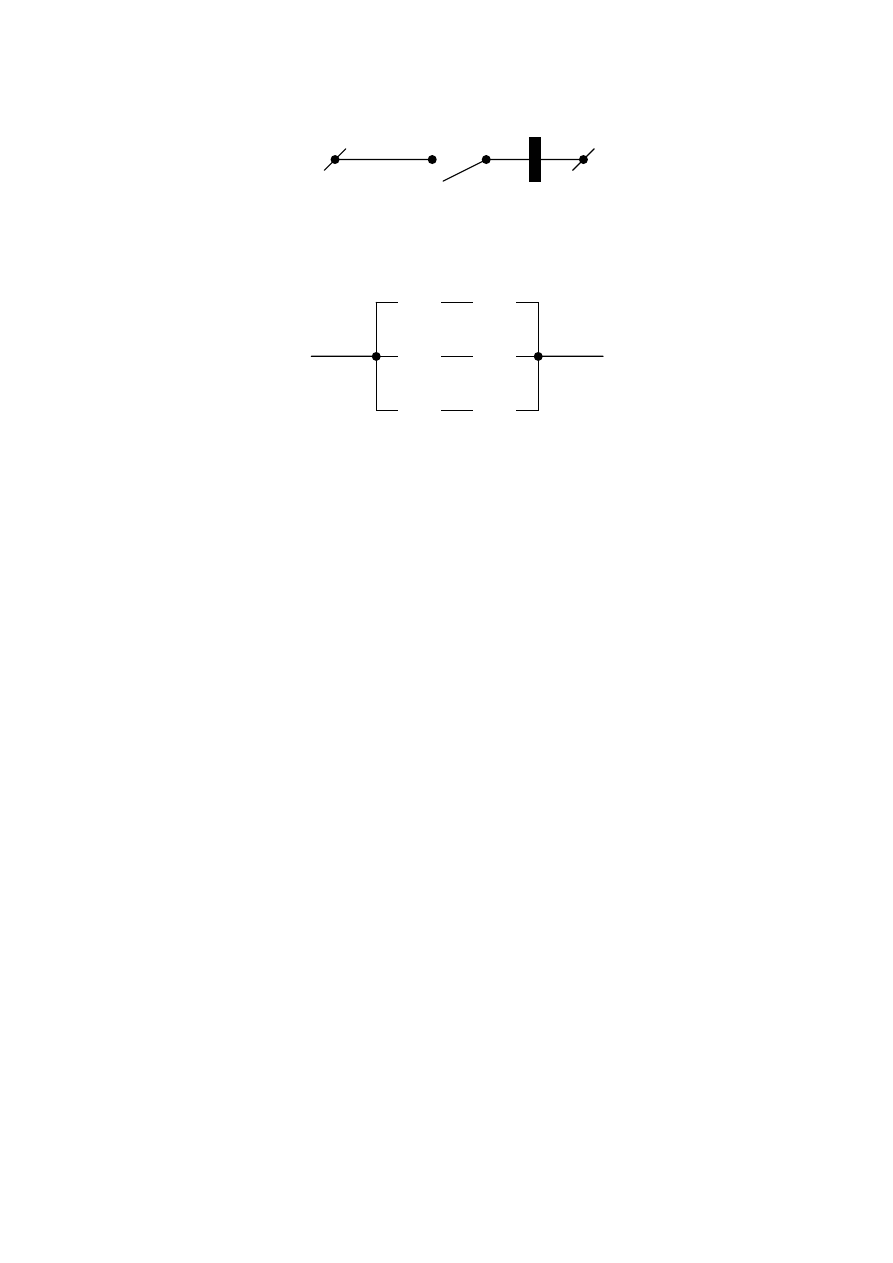
Операция  отрицания   

¬ – способ  построения  такой  цепи, 

проводимость которой противоположна основной. 

а 

b 

а 

b 

55

Рисунок 5.3 

− Инвертирование цепи 

Рисунок 5.3  –  аc 

∨ bā ∨ cb 

ā 

a 

b 

c 

c 

ā 

b