ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 9337
Скачиваний: 24
56
6
БУЛЕВЫ
ФУНКЦИИ
Двоичная функция двоичного аргумента называется
булевой
функцией.
y = f(x
1
, x
2
,…, x
n
), x
i
∈{0,1}, y ∈{0,1}, i = 1,n.
Система булевых функций задается следующим образом:
⎩
⎨
⎧
=
=
).
x
,...,
x
(
f
y
),
x
,...,
x
(
f
y
n
1
k
k
n
1
1
1
Будем говорить, что две функции равны, если их значения
совпадают на любой комбинации значений переменных.
f(x
1
,…, x
n
) = g (x
1
,…, x
n
).
Различными считаются функции, не совпадающие хотя бы
на одной комбинации переменных.
Число различных функций равно
n
2
2
.
Пусть n = 0, тогда
0
2
2
= 2, т.е. функция принимает значение
0
или
1
.
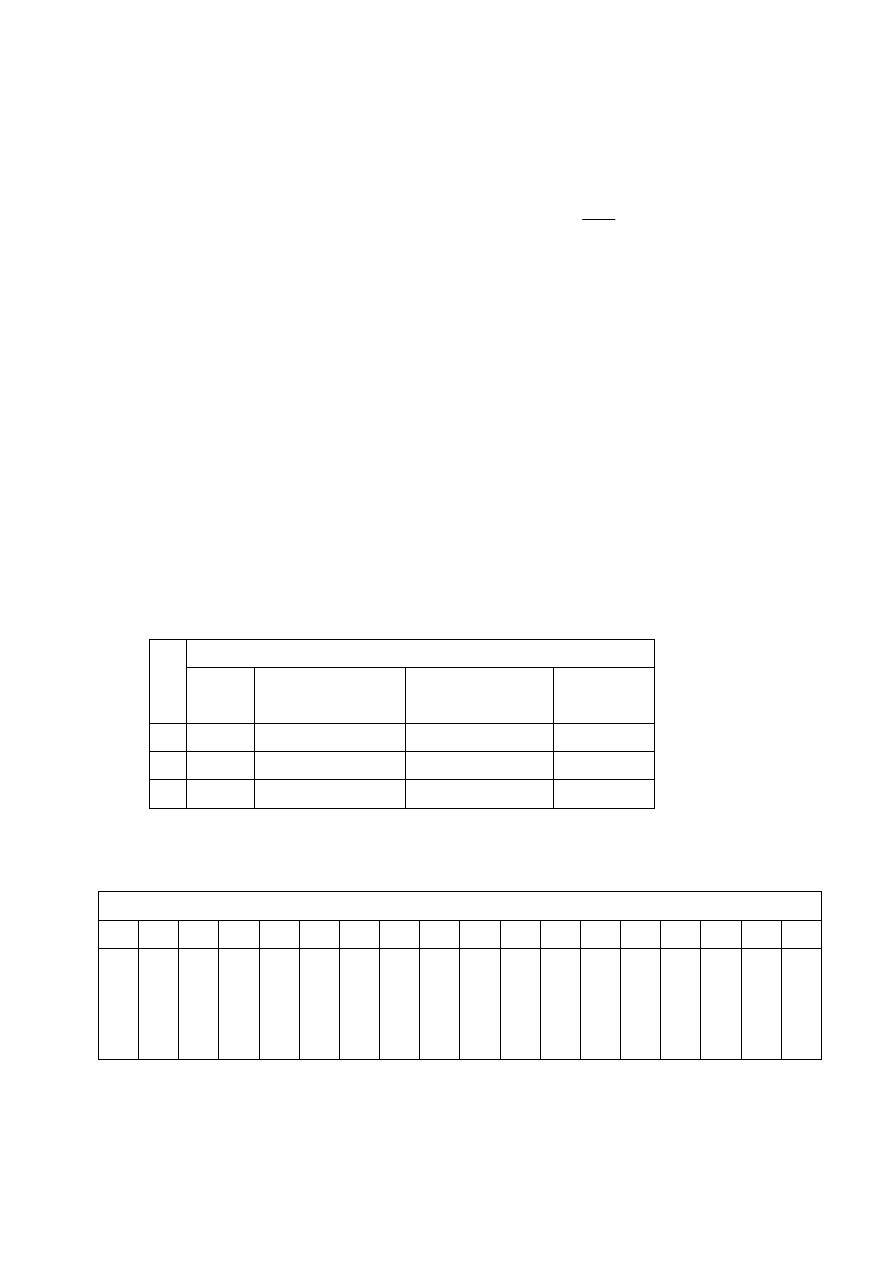
При n=1, число различных функций равно 4.
функция
х
нуль тождествен-
на
отрицатель-
на
едини-
ца
0 0
0
1
1
1 0
1
0
1
0
х
х', ¬x
1
При n=2, число различных функций равно 16.
Функции
х
1
x
2
f
1
f
2
f
3
f
4
f
5
f
6
f
7
f
8
f
9
f
10
f
11
f
12
f
13
f
14
f
15
f
16
0
0
1
1
0
1
0
1
0
0
0
0
0
0
0
1
0
0
1
0
0
0
1
1
0
1
0
0
0
1
0
1
0
1
1
0
0
1
1
1
1
0
0
0
1
0
0
1
1
0
1
0
1
0
1
1
1
1
0
0
1
1
0
1
1
1
1
0
1
1
1
1
Приведем эти булевы функции.
f
1
(x
1
, x
2
) = 0 – константа 0;

57
f
2
(x
1
, x
2
) = x
1
∧ x
2
– конъюнкция;
f
3
(x
1
, x
2
) = x
1
∧
2
x =
2
1
x
x
∨
= x
1
→
/ x
2
– левая коимпликация (читается «не если x
1
,
то x
2
»);
f
4
(x
1
, x
2
) =
1
x
∧
2
x
∨ x
1
∧ x
2
= x
1
;
f
5
(x
1
, x
2
) =
1
x
∧ x
2
= x
1
←
/ x
2
=
2
1
x
x
←
=
2
1
x
x
∨
правая коимпликация;
f
6
(x
1
, x
2
) =
1
x
∧ x
2
∨ x
1
∧ x
2
= x
2
;
f
7
(x
1
, x
2
) =
1
x
∧ x
2
∨ x
1
∧
2
x
= x
1
⊕ x
2
– сложение по моду-
лю два, дизъюнкция с исключением;
f
8
(x
1
, x
2
) = x
1
∨ x
2
– дизъюнкция;
f
9
(x
1
, x
2
) =
1
x
∧
2
x =
2
1
x
x
∨
= x
1
○ x
2
– функция Вебба;
f
10
(x
1
, x
2
) =
1
x
∧
2
x
= x
1
~ x
2
– функция эквивалентности;
f
11
(x
1
, x
2
) =
2
x
– отрицание;
f
12
(x
1
, x
2
) =
1
x
∧
2
x
∨ x
1
∧
2
x
∨ x
1
∧ x
2
=
2
x
∨ x
1
= x
1
←
x
2
– правая импликация (читается «если x
2
, то x
1
»);
f
13
(x
1
, x
2
) =
1
x – отрицание;
f
14
(x
1
, x
2
) =
1
x
∧
1
x
∨
2
x
∧ x
2
∨ x
1
∧ x
2
=
1
x
∨ x
2
= x
1
→
x
2
– левая импликация (читается «если x
1
, то x
2
»);
f
15
(x
1
, x
2
) =
1
x
∧
2
x
∨
1
x
∧ x
1
∧
1
x =
2
x
∨
2
x
= x
1
| x
2
– функция Шеффера;
f
16
(x
1
, x
2
) = 1 – константа 1.
6.1
Способы
задания
булевой
функции
1.
Табличный способ
Область определения булевой функции – совокупность все-
возможных наборов переменных, состоящих из нулей и единиц.
Поэтому для задания булевой функции достаточно задать значе-
ние функции на всех наборах переменных.
Естественным расположением наборов является расположе-
ние в порядке возрастания десятичного числа, соответствующего
данному набору.
58
№ набора
х
1
х
2
х
3
f(х
1
, х
2,
х
3
)
1
2
3
4
5
6
7
8
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
0
1
1
1
0
1
0
1
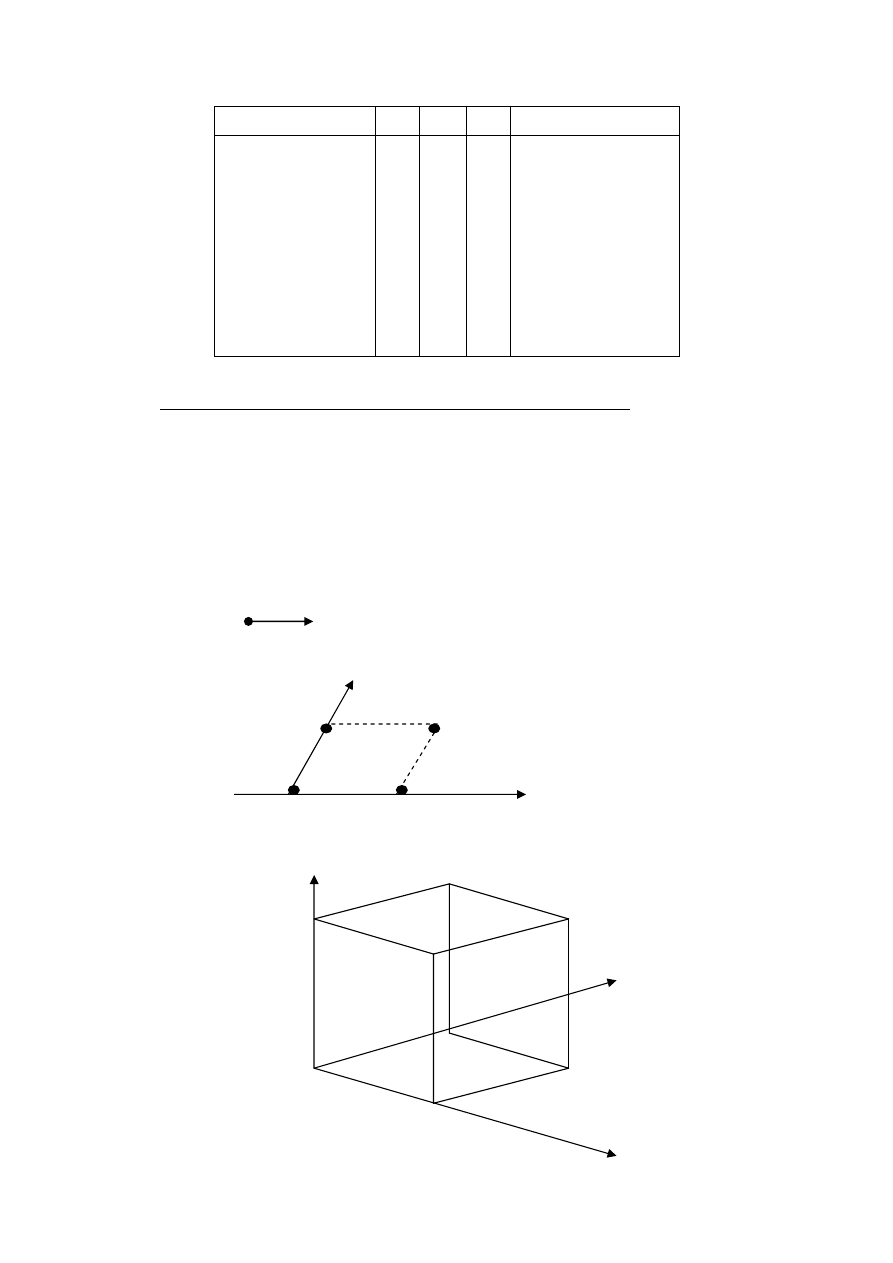
2. Представление вершинами n-мерного куба.
Множество значений вектора x=(x
1
, x
2
,…, x
n
) составляет бу-
лево пространство. Каждому значению вектора сопоставлен эле-
мент пространства. Число компонент вектора определяет размер-
ность пространства.
n = 0
●
n = 1
n = 2
n = 3
x
1
01
00
11
10
x
1
x
2
010
101
011
001
000
111
110
100

59
Расстояние между вершинами n-мерного куба есть число
компонент, значениями которых эти вершины отличаются. Также
расстояние называется
расстоянием по Хемингу
. Соседние вер-
шины n-мерного куба различаются одной компонентой.
3. Задание булевой функции формулами.
Пусть F = {f
1
, f
2
, …, f
n
} – множество булевых функций.
Формулой над F называется выражение вида
F
[F] =
ƒ (t
1
,…, t
n
),
где
ƒ∈F и t
i
, либо переменная, либо формула над F. Множество F
называется
базисом
, функция
ƒ называется
главной (внешней)
операцией (функцией)
, a t
i
называются
подформулами
.
Систему функций будем называть
функционально полной
,
если любая булева функция может быть представлена в виде су-
перпозиции функций этой системы. Функционально полная сис-
тема называется
базисом
. Базис называется
безизбыточным
, ес-
ли ни одну из функций базиса нельзя исключить так, чтобы ос-
тавшаяся система функций была функционально полной. Базис
называется
минимальным
, если он содержит наименьшее из
возможных число функций.
Существует 17 базисов, в каждом из которых нельзя вы-
черкнуть ни одну функцию без потери полноты.
Базис Вебба – { 0 };
Базис Шеффера – { | };
{
→
/ , ~ };
Импликативный базис – {
→, 0};
{
→, →
/ };
{
→
/ , –} – коимпликативный базис;
{
→, ⊕};
{
→, ¯} – импликативный базис;
{&, ¯} – конъюнктивный базис Буля;
{
∨, ¯} – дизъюнктивный базис Буля;
{
→
/ , 1} – коимпликативный базис;
{~, &, 0};
{~,
∨, 0};
{
⊕, &, ~};
{
⊕, ∨, ~};
{
⊕, &, 1} – базис Жегалкина;
{
⊕, ∨, 1}.

60
Техническая реализация базисных функций может быть ос-
нована на использовании различных физических явлений, напри-
мер, импликация и коимпликация может быть основана на ис-
пользовании магнитных явлений, а функции Шеффера и Вебба –
на использовании явлений в полупроводниках.
6.2
Равносильные
преобразования
формул
Две формулы, представляющие одну и ту же функцию, на-
зываются
равносильными.
Преобразования, приводящие неко-
торую формулу к равносильной ей формуле, называются
равно-
сильными
. Булева формула может быть представлена большим
количеством равносильных формул. Некоторые представляют
интерес. Например, формулы, содержащие наименьшее число
букв, или формулы, содержащие только некоторые символы опе-
раций из множества элементарных операций.
Теория булевых функций занимается изучением специаль-
ных функций и равносильных преобразований, приводящих к
этим функциям.
Основные свойства элементарных формул (основные
равносильности):
1.
закон идемпотентности:
а
∨ а = а, а ∧ а = а;
2.
закон коммутативности:
a
∨ b = b ∨ a, a ∧ b = b ∧ a;
3.
закон ассоциативности:
a
∨ (b ∨ c) = (a ∨ b) ∨ c,
a
∧ (b ∧ c) = (a ∧ b) ∧ c;
4.
закон дистрибутивности:
a
∧ (b ∨ c) = a ∧b ∨ a ∧c,
a
∨ (b ∧ c) = (a ∨ b) ∧ (a ∨ c);
5.
закон двойного отрицания:
a
=
а;
6.
закон де Моргана:
7.
законы склеивания:
a
∧b ∨ a ∧ b = а, (a ∨ b) ∧ (a ∨ b ) = а;
;
b
a
b
a
,
b
a
b
a
∨
=
∧
∧
=
∨