ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 9342
Скачиваний: 24
71
x
2
¬x
4
x
2
¬x
3
¬x
1
¬x
2
¬x
3
x
1
x
2
x
4
Пусть
задана
функция
от
пяти
переменных
.
F(x
1
,x
2
,x
3
,x
4
,x
5
) = x
3
¬x
4
x
5
∨ ¬x
1
x
2
¬x
3
¬x
4
∨ ¬x
1
x
2
¬x
4
¬x
5
∨
x
1
¬x
4
¬x
5
∨ x
1
x
2
¬x
3
x
4
∨ x
1
x
2
¬x
4
x
5
∨ ¬x
1
¬
x
2
x
3
¬x
4
¬ x
5
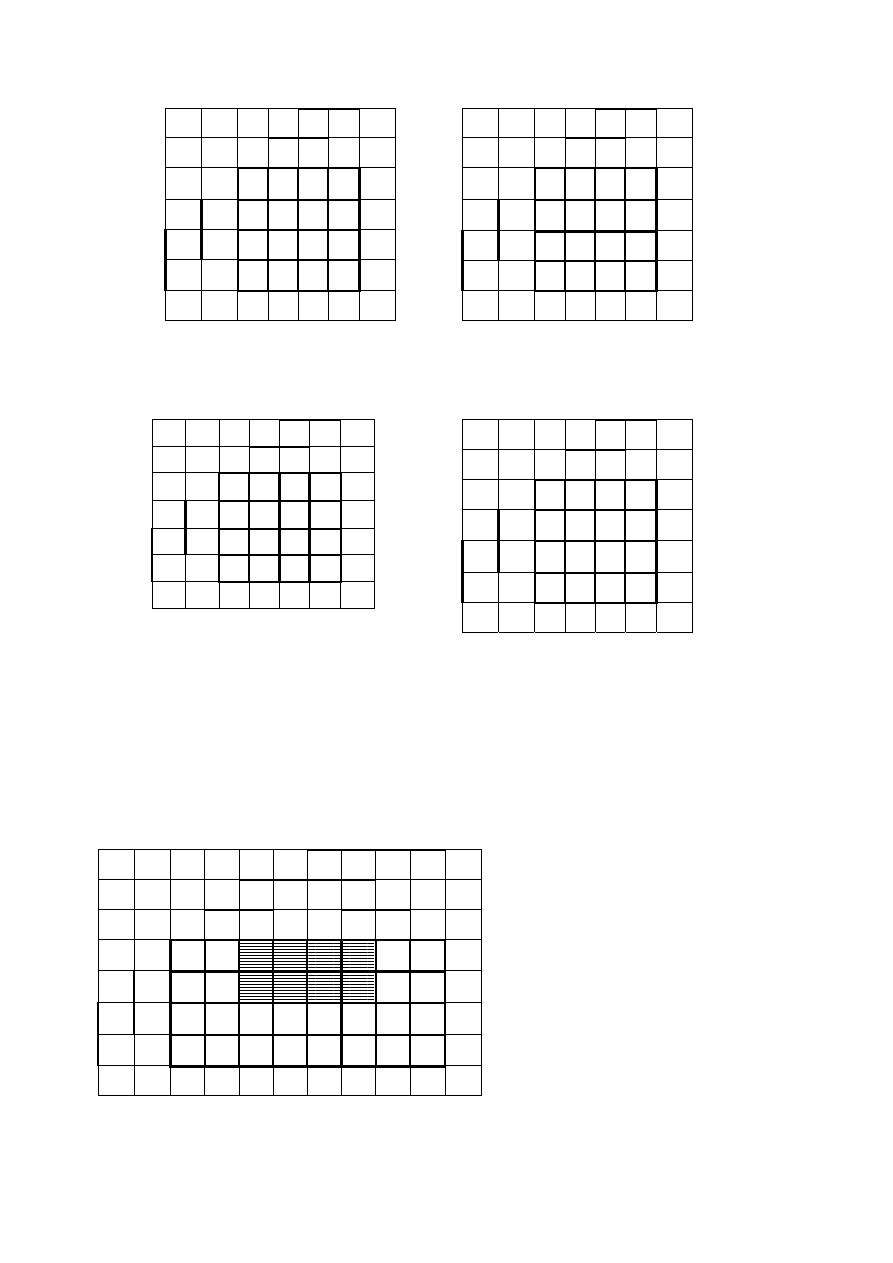
Заданная
функция
отображена
на
карте
Карно
.
Получим
следующие
ин
-
тервалы
: x
2
¬x
4
(
показан
за
-
штрихованной
областью
).
Интервал
x
3
¬x
4
пока
-
зан
ниже
вертикальными
полосами
.
Ниже
представ
-
лены
еще
два
интервала
x
1
¬x
4
¬x
5
, x
1
x
2
¬x
3.
x
1
x
2
• •
• •
x
3
x
4
x
1
x
2
• •
• •
x
3
x
4
x
1
x
2
•
•
x
3
x
4
x
1
x
2
•
•
x
3
x
4
x
1
x
2
x
3
• • • • • • •
• • • • • •
•
•
x
4
x
5

72
В
результате
сокра
-
щенная
функция
,
эквива
-
лентная
исходной
,
запи
-
шется
: F(x
1
,x
2
,x
3
,x
4
,x
5
) =
=x
2
¬x
4
∨ x
3
¬x
4
∨ x
1
¬x
4
¬x
5
∨ x
1
x
2
¬x
3
Простая
импликанта
называется
ядерной,
если
удаление
ее
из
сокращенной
ДНФ
приводит
к
ДНФ
,
которая
не
эквивалентна
исходной
.
Для
каждой
ядерной
импликанты
элементарной
конъ
-
юнкции
существует
такой
набор
значений
переменных
,
который
обращает
конъюнкцию
в
единицу
,
а
остальные
слагаемые
сокра
-
щенной
ДНФ
в
ноль
.
Простая
импликанта
входит
во
все
тупико
-
вые
ДНФ
тогда
и
только
тогда
,
когда
она
входит
в
ядро
функции
.
Для
поиска
импликант
,
входящих
в
ядро
функции
,
исполь
-
зуется
условие
,
состоящее
в
том
,
что
импликанта
,
которая
обра
-
щается
в
единицу
на
тех
же
наборах
переменных
,
что
и
дизъюнк
-
ция
ядерных
импликант
,
в
тупиковую
ДНФ
не
входит
.
Метод
поиска
минимальной
ДНФ
состоит
в
нахождении
минимального
покрытия
булевой
матрицы
.
Булева
матрица
стро
-
ится
следующим
образом
.
В
качестве
строк
берутся
простые
им
-
пликанты
.
В
качестве
столбцов
–
полные
элементарные
конъ
-
юнкции
соответствующие
СДНФ
исходной
функции
.
На
пересе
-
x
1
x
2
x
3
• • • • • • •
• • • • • •
•
•
x
4
x
5
x
1
x
2
x
3
• • • • • • •
• • • • • •
•
•
x
4
x
5

73
чении
строки
и
столбца
ставится
единица
,
если
на
наборе
,
обра
-
щающем
полную
элементарную
конъюнкцию
в
единицу
,
простая
импликанта
также
обращается
в
единицу
.
Далее
подсчитывается
количество
единиц
в
столбце
,
выби
-
рается
столбец
,
количество
единиц
в
котором
минимально
,
и
строка
с
максимальным
количеством
единиц
.
Простая
импликан
-
та
,
соответствующая
выбранной
строке
,
входит
в
покрытие
(
в
яд
-
ро
функции
).
Далее
она
не
рассматривается
.
Из
рассмотрения
удаляются
также
столбцы
,
в
которых
присутствует
единица
в
вы
-
бранной
строке
.
Выбор
осуществляется
до
тех
пор
,
пока
все
столбцы
не
бу
-
дут
покрыты
.
Пример
.
Пусть
задана
функция
:
F(x
1
,x
2
,x
3
,x
4
) = x
1
x
3
∨ x
2
x
3
∨ x
1
x
2
∨ ¬x
1
¬x
2
x
4
∨ ¬x
2
x
3
x
4
∨ x
1
x
3
x
4
Найдем
все
полные
конъюнкции
и
перенумеруем
их
/
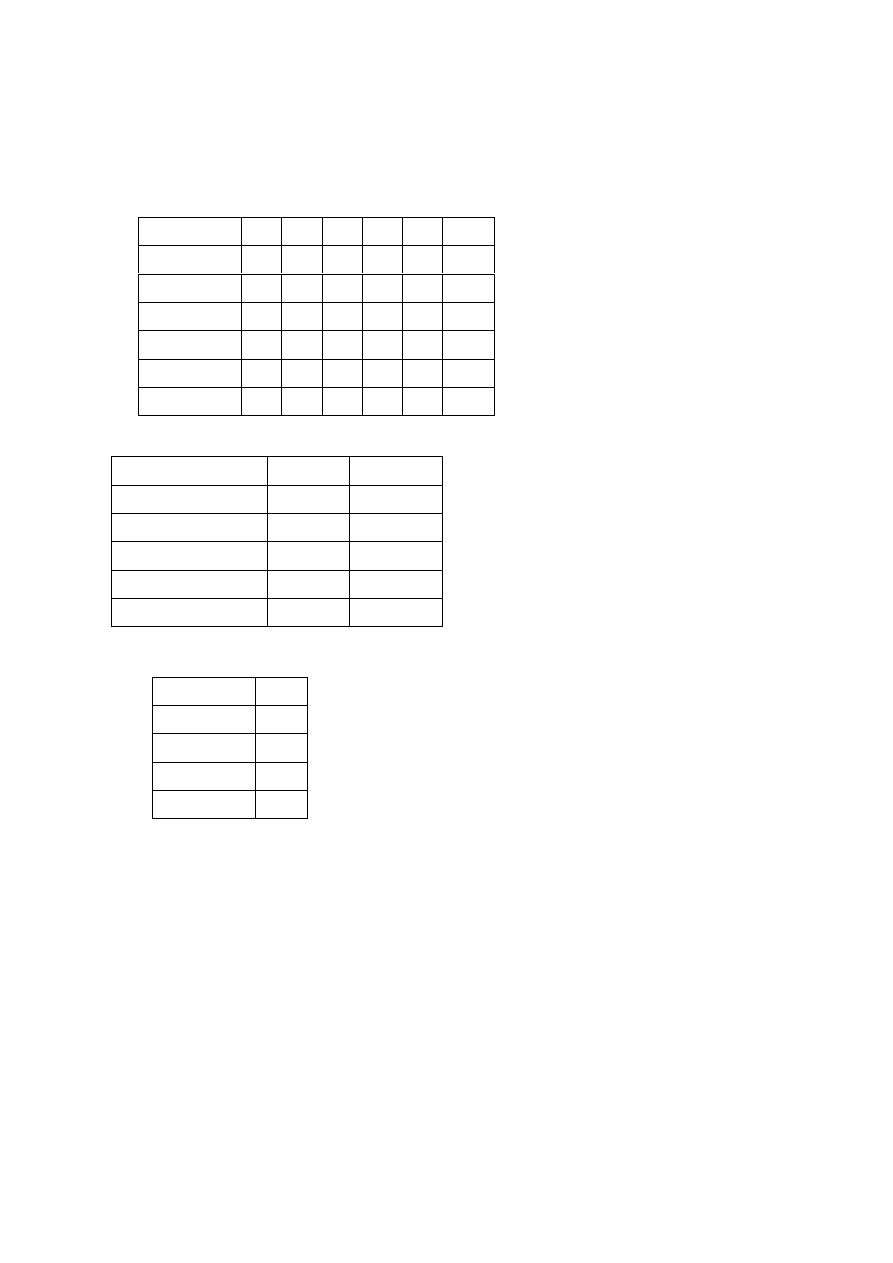
Построим
булеву
матрицу
.
1 2 3 4 5 6 7 8 9 10
x
1
x
3
1 1 1 1
x
2
x
3
1 1 1 1
x
1
x
2
1
1
1
1
¬x
1
¬x
2
x
4
1
1
¬x
2
x
3
x
4
1
1
x
1
x
3
x
4
1
1
2 2 3 1 3 2 1 1 1 2
x
1
x
3
1 ¬x
1
x
2
x
3
x
4
2
¬x
1
x
2
x
3
¬x
4
3
¬x
1
¬x
2
x
3
x
4
4
¬x
1
¬x
2
x
3
¬x
4
x
2
x
3
5 x
1
x
2
x
3
x
4
6
x
1
x
2
x
3
¬x
4
1
¬x
1
x
2
x
3
x
4
2
¬x
1
x
2
x
3
¬x
4
x
1
x
2
5 x
1
x
2
x
3
x
4
6
x
1
x
2
x
3
¬x
4
7
x
1
x
2
¬x
3
x
4
8
x
1
x
2
¬x
3
¬x
4
¬x
1
¬x
2
x
4
3 ¬x
1
¬x
2
x
3
x
4
9
¬x
1
¬x
2
¬x
3
x
4
¬x
2
x
3
x
4
10
x
1
¬x
2
x
3
x
4
3
¬x
1
¬x
2
x
3
x
4
x
1
x
3
x
4
5
x
1
x
2
x
3
x
4
10
x
1
¬x
2
x
3
x
4
74
В
покрытие
обязательно
войдет
четвертый
столбец
и
им
-
пликанта
x
1
x
3
.
Удалим
первую
строку
и
с
первого
по
пятый
столбцы
.
В
результате
получим
матрицу
:
В
оставшейся
части
матрицы
выберем
7
стол
-
бец
и
импликату
x
1
x
2
.
Удалим
выбранную
стро
-
ку
и
столбцы
с
5
по
8.
В
полученной
матрице
вы
-
берем
9
столбец
.
¬x
1
¬x
2
x
4.
В
оставшейся
части
мож
-
но
выбрать
любую
из
строк
.
В
покрытие
войдут
им
-
пликанты
:
x
1
x
3
∨ x
1
x
2
∨ ¬x
1
¬x
2
x
4
∨
x
1
x
3
x
4
Полученное
решение
и
есть
минимальная
ДНФ
.
6.7
Классы
булевых
функций
Суперпозицией системы S={
ϕ
1
(x
1
, x
2
, …, x
k
1
),
ϕ
2
(x
1
, x
2
, …,
x
k
2
), …,
ϕ
l
(x
1
, x
2
, …, x
kl
)}
называется
любая
функция
f,
полученная
:
1)
из
ϕ
j
(x
1
, x
2
, …, x
ki
)
переименованием
переменных
,
ϕ
1
∈ S;
2)
подстановкой
вместо
некоторых
переменных
функции
ϕ
a
(x
1
, x
2
, …, x
ka
),
функций
ϕ
j
(x
1
, x
2
, …, x
kj
),
ϕ
a
,
ϕ
j
∈ S;
3)
с
помощью
многократного
применения
п
.1)
и
2).
Система
S
называется
полной в P
k
,
если
любая
функция
f,
f
∈ P
k
представима
в
виде
суперпозиции
этой
системы
,
и
базисом,
5 6 7 8 9 10
x
2
x
3
1 1
x
1
x
2
1 1 1 1
¬x
1
¬x
2
x
4
1
¬x
2
x
3
x
4
1
x
1
x
3
x
4
1
1
3 2 1 1 1 2
9
10
x
2
x
3
¬x
1
¬x
2
x
4
1
¬x
2
x
3
x
4
1
x
1
x
3
x
4
1
1
2
10
x
2
x
3
¬x
2
x
3
x
4
1
x
1
x
3
x
4
1
2

75
если
теряется
полнота
S
при
удалении
хотя
бы
одной
функции
,
где
P
k
– k–
значная
логика
.
Классы
1. Классом K
0
булевых функций f
i
(x
1
,x
2
, …, x
n
), сохраняющих
константу 0, называется множество функций вида
{f
i
(x
1
,x
2
, …, x
n
)/ f
i
(0,0, …, 0)=0}.
2. Классом K
1
булевых функций f
i
(x
1
,x
2
, …, x
n
), сохраняющих
константу 1, называется множество функций вида
{f
i
(x
1
,x
2
, …, x
n
)/ f
i
(1,1, …, 1)=1}.
3. Классом K
л
линейных булевых функций f
i
(x
1
,x
2
, …, x
n
), на-
зывается множество функций вида
{f
i
(x
1
,x
2
, …, x
n
)/ f
i
(x
1
,x
2
, …, x
n
) =с
0
⊕ Σ c
i
x
i
},
c
0
, c
i
= 0,1; i= 1,2, …n,
где
⊕ Σ –
знаки
операции
«
сложение
по
модулю
два
».
4. Классом K
с
самодвойственных булевых функций f
i
(x
1
,x
2
,
…, x
n
), называется множество функций вида
(
) (
)
(
)
{
}
n
i
n
i
n
i
x
x
x
f
x
x
x
f
x
x
x
f
,...,
,
,...,
,
/
,...,
,
2
1
2
1
2
1
=
5. Классом K
м
монотонных булевых функций f
i
(x
1
,x
2
, …, x
n
)
называется множество функций вида
(
)
(
)
(
)
(
)
(
)
(
)
⎪⎭
⎪
⎬
⎫
⎪⎩
⎪
⎨
⎧
≥
→
=
≥
↔
≥
n
i
n
i
i
i
n
n
n
i
f
f
n
i
x
x
x
f
σ
σ
σ
σ
σ
σ
σ
σ
σ
σ
σ
σ
σ
σ
,...,
,
,...,
,
,...,
2
,
1
,
,...,
,
,...,
,
/
,...,
,
2
1
*
*
2
*
1
*
2
1
*
*
2
*
1
2
1
Критерий полноты.
Система
S
булевых
функций
f
i
является
полной
тогда
и
только
тогда
,
когда
выполняются
пять
условий
:
существуют
:
●
функция
f
i
∈ S,
не
сохраняющая
константу
нуль
: f
i
∉K
0
;
●
функция
f
i
∈ S,
не
сохраняющая
константу
единицу
:
f
i
∉K
1
;
●
нелинейная
функция
в
системе
S;
●
несамодвойственная
функция
в
системе
S;
●
немонотонная
функция
в
системе
S.
.
.