ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 9341
Скачиваний: 24
66
0 0 1 1 x
1
0 1 1 0 x
2
0
1
x
3
Если
вместо
единиц
поставить
черту
,
а
нули
не
писать
,
то
-
гда
эта
же
карта
будет
выглядеть
следующим
образом
:
x
1
x
2
x
3
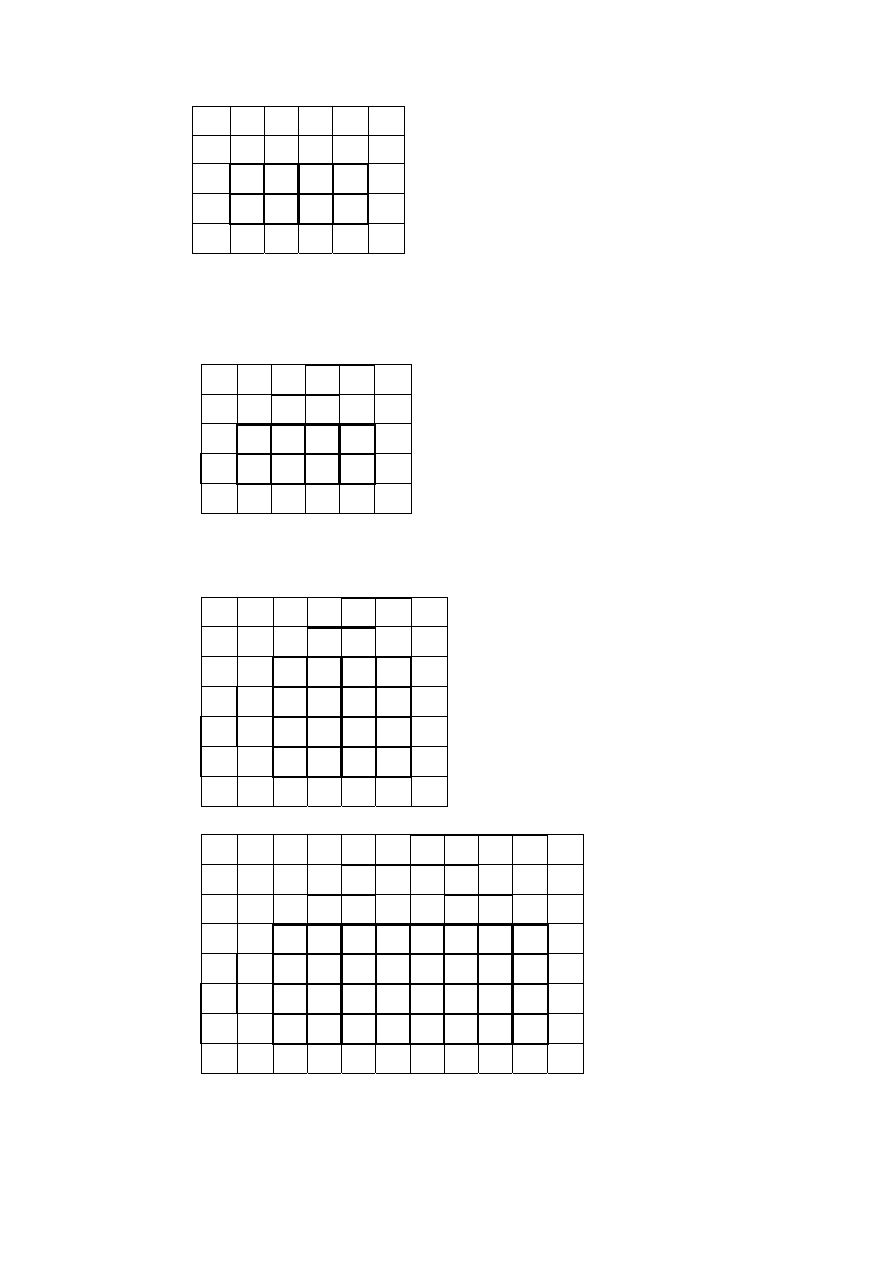
Карты
для
четырех
и
пяти
переменных
представлены
ниже
.
x
1
x
2
x
3
x
4
x
1
x
2
x
3
x
4
x
5

67
Необходимо
отметить
,
что
карта
Карно
обладает
«
зеркаль
-
ной
»
симметрией
и
все
соседние
компоненты
находятся
на
рас
-
стоянии
один
.
Представим
функцию
от
четырех
переменных
картой
Карно
.
Пусть
задана
функция
от
четырех
переменных
в
табличной
фор
-
ме
.
Покажем
наборы
,
на
которых
функция
принимает
единичное
значение
.
Отметим
их
на
карте
точками
.
Зададим
функцию
в
виде
ДНФ
,
представим
ее
картой
Карно
.
F(x
1
x
2
x
3
x
4
) = x
1
x
2
x
4
∨ x
1
¬x
3
x
4
∨ x
3
¬x
4
∨ x
1
x
2
¬x
3
СДНФ
вышеприведенной
функции
запишется
F(x
1
,x
2
,x
3
,x
4
) = x
1
x
2
x
3
x
4
∨ x
1
x
2
¬x
3
x
4
∨ x
1
x
2
¬x
3
¬x
4
∨ x
1
¬x
2
¬x
3
x
4
∨ ¬x
1
¬x
2
x
3
¬x
4
∨ ¬x
1
x
2
x
3
¬x
4
∨ x
1
x
2
x
3
¬x
4
∨ x
1
¬
x
2
x
3
¬
x
4
x
1
x
2
x
3
x
4
F
Наборы
0 0 0 0 0
0 0 0 1 0
0 0 1 0 0
0 0 1 1 0
0 1 0 0 0
0 1 0 1 1 ¬x
1
x
2
¬x
3
x
4
0 1 1 0 1 ¬x
1
x
2
x
3
¬x
4
0 1 1 1 1 ¬x
1
x
2
x
3
x
4
1 0 0 0 0
1 0 0 1 0
1 0 1 0 0
1 0 1 1 0
1 1 0 0 0
1 1 0 1 1 x
1
x
2
¬x
3
x
4
1 1 1 0 0
1 1 1 1 0
x
1
x
2
· ·
·
·
x
3
x
4
x
1
x
2
·
· ·
·
· · · ·
x
3
x
4

68
6.6
Минимизация
булевых
функций
Импликантой
функции
f (x
1
,...,x
n
)
называется
такая
элемен
-
тарная
конъюнкция
К
над
множеством
переменных
{ x
1
,...,x
n
},
что
К
∨ f (x
1
,...,x
n
) = f (x
1
,...,x
n
).
Импликанта
называется
простой,
если
при
отбрасывании
любой
буквы
из
К
получается
элементар
-
ная
конъюнкция
,
не
являющаяся
импликантой
функции
f.
Дизъ
-
юнкция
всех
простых
импликант
функции
f
называется
сокра-
щенной
ДНФ
функции
f.
Дизъюнктивная
нормальная
форма
называется
:
минимальной,
если
она
имеет
наименьшее
число
букв
сре
-
ди
всех
эквивалентных
ей
ДНФ
;
кратчайшей,
если
она
имеет
наименьшую
длину
среди
всех
эквивалентных
ей
ДНФ
;
тупиковой,
если
отбрасывание
любого
слагаемого
или
бук
-
вы
приводит
к
неэквивалентной
ДНФ
.
Тупиковая
ДНФ
функции
f (x
1
,...,x
n
)
получается
из
сокра
-
щенной
ДНФ
этой
функции
путем
отбрасывания
некоторых
эле
-
ментарных
конъюнкций
.
Среди
тупиковых
ДНФ
ищется
мини
-
мальная
и
кратчайшая
ДНФ
функции
.
Существует
несколько
методов
получения
сокращенной
ДНФ
(
получения
простых
импликант
).
Метод
Квайна
.
Для
того
,
чтобы
можно
было
применить
ме
-
тод
Квайна
,
необходимо
,
чтобы
функция
была
приведена
к
виду
СДНФ
.
Основой
метода
является
закон
склеивания
.
a
∧b ∨ a ∧
b
=
а
, (a
∨ b) ∧ (a ∨
b
) =
а
;
1.
Просматриваем
поочередно
пары
конъюнкций
,
если
воз
-
можно
–
производим
склеивание
и
результат
записываем
отдель
-
но
.
Пары
,
участвовавшие
в
склеивании
,
помечаем
.
2.
После
выполнения
всевозможных
склеиваний
в
результат
добавляем
те
конъюнкции
,
которые
не
участвовали
в
склеивании
.
3.
Если
не
было
элементарных
конъюнкций
,
которые
можно
было
склеивать
,
то
алгоритм
закончен
.
В
противном
случае
пе
-
реходим
к
пункту
1.
Пример
.

69
Пусть
задана
функция
F(x
1
,x
2
,x
3
,x
4
) = x
1
x
2
x
3
x
4
∨ x
1
x
2
¬x
3
x
4
∨ x
1
x
2
¬x
3
¬x
4
∨ x
1
¬x
2
¬x
3
x
4
∨ ¬x
1
¬x
2
x
3
¬x
4
∨ ¬x
1
x
2
x
3
¬x
4
∨ x
1
x
2
x
3
¬x
4
∨ x
1
¬
x
2
x
3
¬
x
4
Произведем
всевозможные
склеивания
,
в
результате
полу
-
чим
:
F(x
1
,x
2
,x
3
,x
4
) = x
1
x
2
x
4
∨ x
1
x
2
x
3
∨ x
1
x
2
¬x
3
∨ x
1
¬x
3
x
4
∨ x
1
x
2
¬
x
4
∨ ¬x
1
x
3
¬x
4
∨ ¬x
2
x
3
¬x
4
∨ x
2
x
3
¬x
4
∨ x
1
x
3
¬x
4
Все
конъюнкции
исходной
функции
участвовали
в
склеива
-
нии
.
Произведем
склеивание
еще
раз
.
Конъюнкция
x
1
¬x
3
x
4
в
склеивании
не
участвовала
,
поэтому
записываем
ее
в
результат
.
F(x
1
,x
2
,x
3
,x
4
) = x
1
x
2
∨ x
3
¬x
4
∨ x
1
¬x
3
x
4
Метод Блейка
Метод
Блейка
позволяет
получить
сокращенную
ДНФ
из
произвольной
ДНФ
и
состоит
в
применении
правил
обобщенного
склеивания
(xK
1
∨ ¬xK
2
= xK
1
∨ ¬xK
2
∨ K
1
K
2
)
и
поглощения
(K
1
∨ K
1
K
2
= K
1
).
На
первом
этапе
производятся
операции
обобщенного
склеивания
до
тех
пор
,
пока
это
возможно
.
На
втором
–
операции
поглощения
.
Пример
.
Получить
сокращенную
ДНФ
для
функции
F(x
1
,x
2
,x
3
) = x
1
x
2
∨ ¬ x
1
x
3
∨
¬x
2
x
3
После
первого
этапа
получим
:
F(x
1
,x
2
,x
3
) = x
1
x
2
∨ ¬ x
1
x
3
∨ x
2
x
3
∨
¬x
2
x
3
∨ x
1
x
3
∨ x
3
После
второго
:
F(x
1
,x
2
,x
3
) = x
1
x
2
∨ x
3
Если
функция
задана
в
КНФ
,
для
получения
сокращенной
ДНФ
нужно
сначала
раскрыть
скобки
,
пользуясь
законом
дист
-
рибутивности
,
затем
из
полученной
ДНФ
вычеркнуть
буквы
и
слагаемые
,
используя
законы
: ¬ x
1
x
1
=0, x
1
∨x
1
= x
1
, x
1
x
1
= x
1
, K
1
∨
K
1
K
2
= K
1
.
Для
небольших
значений
n
сокращенную
ДНФ
функции
f
(x
1
,...,x
n
)
можно
находить
с
помощью
карт
Карно
.
Объединяя
клетки
,
соответствующие
единичным
значениям
функции
f,
в

70
максимальные
интервалы
и
сопоставляя
им
элементарные
конъ
-
юнкции
,
получим
сокращенную
ДНФ
.
Рассмотрим
на
примере
функции
от
четырех
переменных
объединение
в
максимальные
интервалы
.
Пусть
функция
принимает
единичное
значение
на
всех
на
-
борах
переменных
.
Функция
тождественно
равна
единице
.
При
объединении
необходимо
придерживаться
правил
:
•
в
объединение
включаются
только
клетки
«
зеркально
»
симметричные
относительно
какой
-
либо
из
осей
;
•
количество
клеток
соответствует
степени
2 (2,4, 8, 16,...).
В
первом
случае
результат
объединения
равен
x
1
,
во
втором
–
x
2
.
Результат
– ¬ x
4
¬ x
2
¬x
4
x
1
x
2
• •
• •
• •
• •
x
3
x
4
x
1
x
2
• •
• •
• •
• •
x
3
x
4
x
1
x
2
• • • •
• • • •
x
3
x
4
x
1
x
2
• •
• •
x
3
x
4