ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 6744
Скачиваний: 28

86
ний будущего устройства. Точное число входов и выходов системы
управления известно, так как каждый вход ее есть выход некоторого
датчика, установленного на объекте управления или на пульте
управления (в этом случае датчиком является человек-оператор), а
каждый выход ее есть вход некоторого исполнительного механизма
на объекте управления или индикатора сигнализации на пульте.
Разработчику известно смысловое значение всех входов x
i
и
выходов y
j
. Часто на практике x
i
и y
j
принимают двоичные значения,
например, x
i
- «включено», «выключено»; y
j
- «включить», «выклю-
чить». Сигнал по входу или по выходу может быть и недвоичным,
но дискретным. Например, датчик температуры показывает три
уровня : 1) ниже - 5
o
C; 2) от -5
o
С до +5
o
С; 3) выше +5
o
С. В этом слу-
чае вместо одного входа x от датчика температуры введем два: x
i
׳ и
x
i
״. При этом возможны четыре комбинации двоичных значений на
этих входах: 00, 01, 10, 11. Три из них можно сопоставить трем сиг-
налам от датчика температуры.
Будем обозначать через X
i
набор значений входных сигналов и
Y
j
− набор значений выходных сигналов. Если, например, устройст-
во имеет три входа и в некоторый момент времени x
1
= 1, x
2
= 0,
x
3
= 0, то двоичный номер этого набора есть 100. Таким образом,
этому набору соответствует вход X
4
.
Составим теперь таблицу, в левой части которой перечислены
все входные наборы, а в правой
− соответствующие им выходные
наборы. Если устройство управления имеет q входов и p выходов, то
таблица будет содержать 2
q
строк, а в правой ее части будут пере-
числены выходы из 2
p
возможных. Заметим, что заполнить такую
таблицу можно только тогда, когда каждый набор X
i
однозначно
определяет набор Y
j
. Если это так, то говорят, что система управле-
ния представляет собой комбинационную схему (автомат без памя-
ти). Сама таблица называется автоматной таблицей и дает авто-
матное описание системы управления.
Приведем пример составления автоматной таблицы. Пусть не-
обходимо спроектировать следующую систему управления. Конди-
ционер малой мощности должен включаться, если температура воз-
духа в помещении достигнет +10
o
С и выключаться, когда темпера-
тура достигнет +22
o
С. После этого должен включиться мощный
кондиционер. Если же температура достигнет +30
o
С, необходимо

87
включить оба кондиционера. Наконец если температура достигнет
значения +35
o
С, необходимо выдать аварийный сигнал.
Исходя из условий задачи, можно считать, что проектируемое
устройство имеет один вход, принимающий пять значений:
1) t
o
< 10
o
C; 2) +10
o
C
≤ t
o
< +22
o
C; 3) +22
o
C
≤ t
o
< +30
o
C;
4) +30
o
C
≤ t
o
< +35; 5) t
o
≥ 35
o
C.
Для перехода к двоичным входным сигналам введем три входа:
x
1
, x
2
, x
3
. На них можно реализовать 8 различных двоичных комби-
наций. Выберем любые пять из них (например, 000, 001, 010, 011,
100) и закодируем ими упомянутые показания датчика температуры.
Выходами устройства управления являются три двоичных сиг-
нала: y
1
, y
2
, y
3
. Значение y
1
= 1 соответствует включению кондицио-
нера малой мощности, y
1
= 0
− отключению этого кондиционера,
y
2
= 1
− включению кондиционера большой мощности, y
2
= 0
− его
отключению, y
3
= 1 соответствует включению сигнала аварии, y
3
= 0
− отсутствию этого сигнала. Теперь можно составить автоматную
таблицу (табл. 3.9). Эта таблица имеет две особенности: 1) в правой
части не заполнены три последние строки; 2) для набора X
4
не опре-
делен однозначно выходной набор.
Таблица 3.9 - Автоматная таблица
Входы
Выходы
x
1
x
2
x
3
y
1
y
2
y
3
0
0 0 0 0 0
0
0 1 1 0 0
0
1 0 0 1 0
0
1 1 1 1 0
1
0 0 ? ? 1
1
0 1
1
1 0
1
1 1
Действительно, входные наборы 101, 100, 111 не соответству-
ют никакому сигналу от датчика температуры и никогда не появля-
ются на входе системы управления. Такие наборы входов называют-
ся неиспользуемыми (о том, как заполнять таблицу в этом случае,
скажем позднее). Кроме того, из задания неясно, что делать с кон-
диционерами, если температура стала аварийной (входной набор
100): оставить включенными (соответствующий выходной набор
88
010
001
011
000
010
011
000
001
000
100
001
100
010
100
011
100
000
001
010
011
Z
1
Z
0
Z
3
Z
2
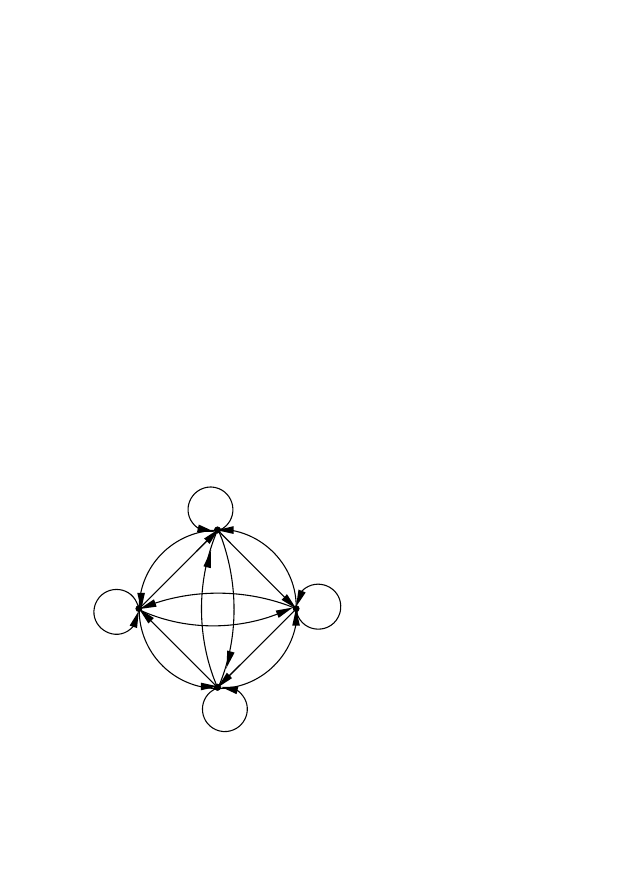
Рис. 3.2 – Граф переходов
111), отключить (выходной набор 001), либо оставить включенным
один из них (выходные наборы 101, 011). После уточнения этого
вопроса (с заказчиком) неоднозначность должна быть устранена.
Возможна ситуация, когда разработчику не удается составить
таблицу так, чтобы каждому входному набору в ней соответствовал
единственный выходной набор. В этом случае мы имеем дело с ав-
томатом с памятью. Так, для нашего примера на вопрос разработ-
чика о том, что нужно выдавать при входном наборе 100, заказчик
может ответить, что это зависит от состояния исполнительных ме-
ханизмов в момент возникновения аварийной ситуации. Если кон-
диционеры были включены, то следует оставить их включенными, а
если они не были включены, то включать их не следует. При таком
ответе неоднозначность в таблице устранить не удастся. Есть два
способа выхода из положения:
1) увеличить число входов системы управления, дополнив их
сигналами датчиков, регистрирующих состояние каждого конди-
ционера;
2) в системе управления организовать память, в которой будут
фиксироваться действия, которые она формировала в прошлом.
Формально это означает введение множества внутренних состояний
системы. Обозначим это множество Z = {z
0
, z
1
,...,z
k
}. Среди элемен-
тов множества Z выделим
начальное состояние объ-
екта z
0
. В каждой конкрет-
ной задаче начальное со-
стояние связывается с не-
которым фиксированным
состоянием объекта.
В нашем примере с конди-
ционерами
множество
внутренних
состояний
Z = {z
0
, z
1
, z
2
, z
3
}. Началь-
ное состояние z
0
соответ-
ствует ситуации, когда оба
кондиционера выключены,
z
1
− включенному конди-
ционеру малой мощности
и выключенному конди-

89
ционеру большой мощности, z
2
− включенному кондиционеру
большой мощности и выключенному кондиционеру малой мощно-
сти, z
3
− состояние, когда оба кондиционера включены.
Построим граф переходов рассматриваемого автомата с памя-
тью. Вершинами графа являются состояния z
0
, z
1
, z
2
, z
3
, дуги соот-
ветствуют переходам из одного состояния в другое. Каждая дуга
помечается входным набором, при котором осуществляется соот-
ветствующий переход (рис. 3.2). Петлям графа соответствуют два
набора, что следует из условий задачи и уточнений заказчика.
Информацию о смене состояний можно представить в виде так
называемой таблицы переходов (для нашего примера это табл.
3.10). На пересечении строк и столбцов этой таблицы стоят внут-
ренние состояния, в которые переходит система при данной комби-
нации внутреннего состояния и входного набора.
Таблица 3.10 – Таблица переходов
Состояния
Входы
000 001 010 011 100
Z
0
Z
0
Z
1
Z
2
Z
3
Z
0
Z
1
Z
0
Z
1
Z
2
Z
3
Z
1
Z
2
Z
0
Z
1
Z
2
Z
3
Z
2
Z
3
Z
0
Z
1
Z
2
Z
3
Z
3
Таблица переходов еще не содержит полной информации о ра-
боте системы управления: необходимо указать, как формируются
выходные наборы, подаваемые системой управления на объект. Для
этого таблицу или граф переходов нужно дополнить таблицей вы-
ходов. В случае нашего примера она имеет вид табл. 3.11.
Таблица 3.11 – Таблица выходов
Состояния
Входы
000 001 010 011 100
Z
0
000
100
010
110
001
Z
1
000 100 010 110 101
Z
2
000 100 010 110 011
Z
3
000 100 010 110 111

90
В отличие от таблицы переходов, на пересечении строк и
столбцов таблицы выходов указаны выходные наборы, формируе-
мые системой управления.
Таблицы переходов и выходов называются автоматными таб-
лицами. Задание таких таблиц является одной из форм автоматно-
го описания системы управления.
Если на дугах графа переходов выписать еще и выходные на-
боры, соответствующие входному набору и внутреннему состоянию,
из которого эта дуга выходит, то мы получим полное задание систе-
мы управления. Такой граф называется автоматным графом и дает
еще одно автоматное описание, эквивалентное табличному. Однако
каждая из этих форм автоматного описания имеет свои преимущест-
ва. Таблицы дают возможность осуществить формальный переход к
структуре системы управления. С другой стороны, автоматный граф
позволяет судить о том, полно ли сформулированы условия функ-
ционирования системы управления и нет ли противоречий в форму-
лировке задания. Неполнота задания проявляется в наличии в графе
вершин, из которых при некоторых входных наборах не указаны
дуги переходов. Противоречивость может выявляться либо в нали-
чии двух одинаково помеченных дуг, ведущих из одной вершины в
разные, либо в том, что одной и той же дуге и входному набору со-
поставляется более одного выходного набора.
3.7
Синтез
комбинационных
схем
С помощью аппарата булевых функций можно получить наи-
более компактное автоматное описание системы управления. Кроме
того, этот аппарат может быть эффективно использован при перехо-
де от автоматного описания к структурной реализации системы
управления. Приведем одну из методик синтеза комбинационной
схемы с одним выходом, основанную на исходном представлении в
виде совокупности таблиц истинности булевых функций. Для пол-
ноты изложения перечислим все этапы проектирования, хотя неко-
торые из них уже были рассмотрены ранее.