ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 6745
Скачиваний: 28

91
Первый этап. 1. По заданному в техническом задании алго-
ритму выделяем независимые аргументы (входы) и выписываем все
их комбинации (входные наборы). При большом количестве входов
следует попытаться объединить их или реализовать устройство по
частям.
2. Отмечаем запрещенные наборы, т.е. комбинации входных
сигналов, которые не могут возникнуть.
3. Выписываем все значения выхода для каждого незапрещен-
ного набора. При этом нужно проверить, зависит ли это значение
только от комбинации входов, или еще и от последовательности их
появления в каждой комбинации. В первом случае получим таблицу
истинности. Во втором случае делаем вывод о том, что заданный
алгоритм нельзя реализовать с помощью комбинационного устрой-
ства.
4. Доопределяем таблицу на запрещенных наборах, пользуясь
информацией, имеющейся в алгоритме, либо руководствуясь сле-
дующим (не всегда наилучшим) соображением: если в таблице
больше единичных значений выхода, чем нулевых, она доопределя-
ется единичными значениями и наоборот.
5. Записываем аналитическое выражение выхода как булевой
функции входов в совершенной ДНФ, если единичных значений
выхода в таблице меньше, и в совершенной КНФ
− в противном
случае.
Второй этап. 6. Упрощаем полученное выражение. Для этой
цели можно либо использовать известные методы минимизации бу-
левых функций, дающее минимально возможное в некотором
смысле выражение, либо применить систему эквивалентных преоб-
разований. Дополним уже знакомые нам эквивалентные преобразо-
вания следующими соотношениями:
(x
1
٧ x
2
) (x
2
٧ x
3
) (x
3
٧
⎯x
1
) = (x
1
٧ x
2
) (x
3
٧
⎯x
1
),
x
1
x
2
٧ x
2
x
3
٧ x
3
⎯x
1
= x
1
x
2
٧ x
3
⎯x
1
,
ƒ (x
1
, x
2
,...,x
n
) = x
1
ƒ (1, x
2
,...,x
n
) ٧
⎯x
1
ƒ (0, x
2
,...,x
n
),
ƒ (x
1
, x
2
,...,x
n
) = (x
1
٧
ƒ (0, x
2
,...,x
n
)) (
⎯x
1
٧
ƒ (1, x
2
,...,x
n
)),
x
1
ƒ (x
1
, x
2
,...,x
n
) = x
1
ƒ (1, x
2
,...,x
n
),
x
1
٧
ƒ (x
1
, x
2
,...,x
n
) = x
1
٧
ƒ (0, x
2
,...,x
n
),
⎯x
1
ƒ (x
1
, x
2
,...,x
n
) =
⎯x
1
ƒ (0, x
2
,...,x
n
),
⎯x
1
٧
ƒ (x
1
, x
2
,...,x
n
) =
⎯x
1
٧
ƒ (1, x
2
,...,x
n
).
92
Эффект применения эквивалентных преобразований зависит от
последовательности их применения. Наиболее важными являются
склеивание x
i
٧
⎯x
i
= 1 и поглощение x
i
٧ x
i
x
j
= x
i
. К сожалению,
нельзя указать такой порядок применения эквивалентных преобра-
зований, который обеспечивал бы наиболее простую форму записи
булевой функции.
Третий этап. 7. Пользуясь таблицами, имеющимися в литера-
туре, преобразуем полученные на втором этапе выражения в такие,
логические операции которых соответствуют выбранному функцио-
нально полному набору элементов. При этом следует иметь в виду,
что в новом базисе минимальность выражения не гарантируется.
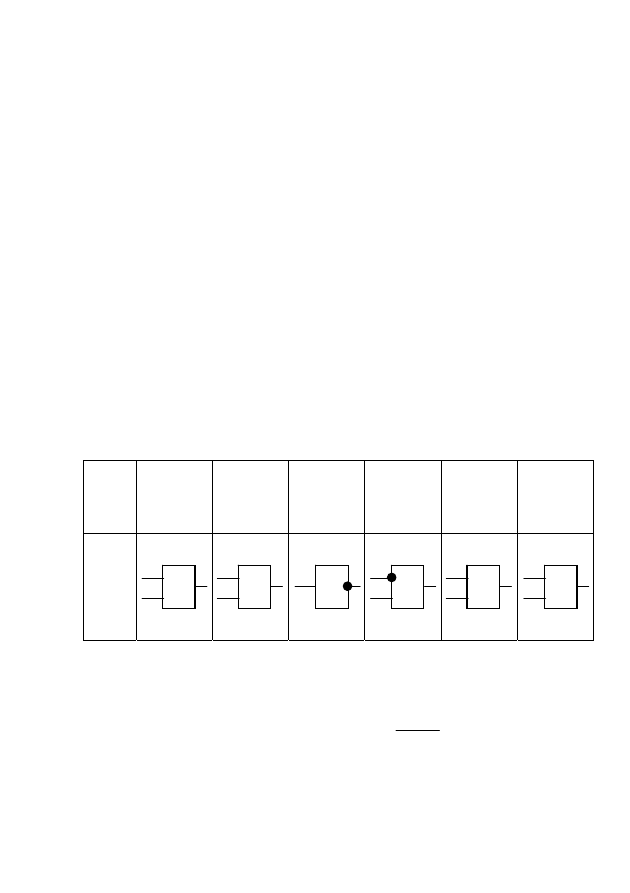
8. Выбираем обозначение для каждой логической операции,
реализуемой элементами данного набора. Существуют стандартные
изображения базисных функций как некоторых блоков, техническая
реализация которых может быть основана на использовании различ-
ных физических явлений: магнитных, явлений в полупроводниках и
т.д. Примеры таких символических обозначений представлены в
таблице 3.12.
Таблица 3.12 – Логические элементы и их обозначения
Эле-
мент
Дизъ-
юнкция
x
1
٧ x
2
Конъ-
юнкция
x
1
· x
2
Отрица-
ние
⎯x
Импли-
кация
x
1
→ x
2
Эквива-
лент-
ность
x
1
~ x
2
Сложе-
ние по
mod 2
x
1
⊕ x
2
Обо-
зна-
чение
9. По аналитическому выражению строим логическую схему.
При этом необходимо соблюдать очередность, раскрывая выраже-
ние «изнутри наружу». Полученная в результате логическая схема
может оказаться избыточной. Например, пусть имеем минимальное
выражение булевой функции y = (x
1
٧ x
2
) x
3
٧ (x
1
٧ x
2
) x
4
. Переходя к
логической схеме, получим шесть элементов, причем два из них
реализуют функцию x
1
٧ x
2
. Поэтому нужно постараться упростить
x
1
x
2
x
1
x
2
x
x
1
x
2
x
1
x
2
x
1
x
2
1
&
1
1
=
M2
93
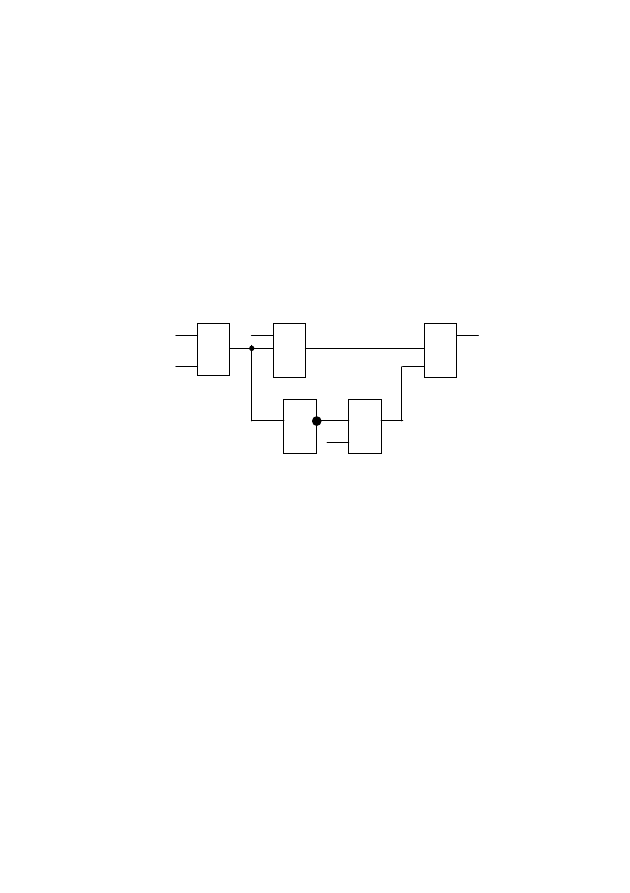
логическую схему, находя общие части выражения и объединяя их в
схеме. Для нашего примера окончательно получим схему, изобра-
женную на рис. 3.3.
Четвертый этап. 10. От логической схемы выражения, описы-
вающего работу системы управления, можно непосредственно пе-
рейти к принципиальной схеме устройства, так как каждому услов-
ному изображению функции на логической схеме соответствует фи-
зический элемент, реализующий данную операцию и имеющий не-
сколько вариантов принципиальной схемы в зависимости от эле-
ментной базы. Соединения между элементами задаются связями на
логической схеме.
x
1
x
2
x
3
y
x
4
1
&
1
&
1
Рис. 3.3 – Логическая схема
3.8
Логика
предикатов
3.8.1
Предикаты
и
операции
квантирования
Развитием уже знакомой нам алгебры высказываний является
логика предикатов, Это тоже логическая система или определенный
язык описания знаний. В логике предикатов наряду с высказыва-
ниями рассматриваются некоторые высказывательные функции,
называемые предикатами.
Рассмотрим вначале некоторые примеры:
1) «x
− простое число». Это выражение не является высказыва-
нием, пока мы не заменим переменную x на какое-либо определен-
ное число. При x = 1 получим истинное высказывание, при x = 6
−
ложное. Таким образом, выражение «x
− простое число» есть неко-
торая функция P (x), зависящая от переменной x. Область определе-

94
ния P (x)
− множество чисел, область значений P (x) − высказыва-
ния;
2) «x больше y». Это выражение можно рассматривать как
функцию Q (x, y), зависящую от переменных x и y. Она становится
высказыванием после того, как x и y заменим их значениями.
В общем случае под предикатом от n переменных понимает-
ся выражение P(x
1
, x
2
,.., x
n
), которое становится высказыванием по-
сле подстановки вместо переменных x
1
, x
2
,.., x
n
их значений из мно-
жеств M
1
, M
2
,..., M
n
соответственно. Элементы этих множеств на-
зываются предметами, а переменные x
1
, x
2
,.., x
n
− предметными
переменными. Множество M
1
× M
2
×…× M
n
(декартово произведе-
ние) упорядоченных наборов длины n называется полем предиката
P (x
1
, x
2
,.., x
n
). Если число предметных переменных равно нулю, то
предикат есть высказывание.
Будем обозначать:
x, y, z,.., x
1
, x
2
, x
3
,... (малые буквы конца латинского алфавита)
−
предметные переменные;
a, b, c,.., a
1
, a
2
, a
3
,... (малые буквы начала латинского алфавита)
− предметы из множеств M
1
, M
2
,.., M
n
;
A (x), B, F (x, y), P (x
1
, x
2
,.., x
n
)
− предикаты. Символы 0,1, как и
прежде, обозначают истину и ложь.
К предикатам можно применять операции алгебры высказыва-
ний (конъюнкцию, дизъюнкцию, импликацию, эквивалентность,
отрицание) и получать новые предикаты. Это действительно так:
заменяя предметные переменные в предикатах их значениями из
некоторого множества предметов, мы получим высказывания ис-
тинные или ложные, а применяя к ним операции логики высказыва-
ний, получим новые высказывания.
Пусть, например, «х = у»
− предикат A (х, у), а «х < у» − преди-
кат В (х, у). Тогда
A (x, y) ٧ B (x, y)
− новый предикат, полученный применением операции дизъюнк-
ции.
Помимо операций алгебры высказываний в логике предикатов
есть две специфические операции, связанные с природой предика-
тов.
Пусть дан предикат P (x), зависящий от одной переменной и
определенный на поле М.

95
Выражение
∀x P (x) («для всякого х, Р (х)») означает высказы-
вание, истинное только в том случае, когда предикат Р (х) истинен
для всех предметов из поля М. Здесь символ
∀ − квантор общно-
сти.
Выражение
∃x P (x) («существует х такой, что Р (х)») означает
высказывание, истинное только в том случае, когда предикат Р (х)
истинен хотя бы для одного предмета из поля М; символ
∃ − кван-
тор существования.
Эти две операции называются операциями квантирования. Рас-
смотрим примеры применения операций квантирования. Пусть даны
предикаты над полем натуральных чисел:
1) x
2
= xx, тогда
∀x (x
2
= xx)
− истинное высказывание;
2) x + 2 = 7, тогда
∀x (x + 2 = 7) − ложное;
∃x (x + 2 = 7) − истинное;
3) x + 2 = x, тогда
∃x (x + 2 = x) − ложное.
Операции квантирования легко обобщаются на случай, когда
предикат зависит от n переменных. Пусть G (x
1
, x
2
,.., x
n
)
− предикат
от переменных x
1
, x
2
,.., x
n
над полем М = M
1
× M
2
×..× M
n
. Подста-
вим вместо переменных x
1
,.., x
i-1
, x
i+1
,.., x
n
предметы a
1
,.., a
i-1
, a
i+1
,.., a
n
из множеств M
1
,.., M
i-1
, M
i+1
,.., M
n
. Получим предикат G (a
1
,.., a
i-1
,
x
i
, a
i+1
,.., a
n
), зависящий только от одной переменной x
i
. Cледова-
тельно, выражение
∀x
i
G (a
1
,.., a
i-1
, x
i
, a
i+1
,.., a
n
)
есть высказывание. Отсюда выражение
∀x
i
G(x
1
,.., x
i-1
, x
i
, x
i+1
,.., x
n
)
есть предикат от n-1 переменной. Он не зависит от x
i
. Значение его
для данного набора (a
1
,.., a
i-1
, a
i+1
,.., a
n
) равно истине, если пре-
дикат G (a
1
,.., a
i-1
, x
i
, a
i+1
,.., a
n
) истинен для всякого предмета из
поля М.
Аналогичные рассуждения можно провести для квантора
∃. С
помощью операций конъюнкции, дизъюнкции, импликации, эквива-
лентности, отрицания, а также операций квантирования можно по-
лучать более сложные предикаты. При этом предметные перемен-
ные, по отношению к которым применялись операции квантирова-
ния, называются связанными а остальные
− свободными.
Например, в предикате
∀x (A (x, y) ٧ ∃z B (z, v))